Difference between revisions of "Aufgaben:Exercise 2.4Z: LZW Coding and Decoding again"
| Line 3: | Line 3: | ||
}} | }} | ||
| − | [[File:EN_Inf_Z_2_4.png|right|frame| | + | [[File:EN_Inf_Z_2_4.png|right|frame|Snapshots of the LZW dictionaries]] |
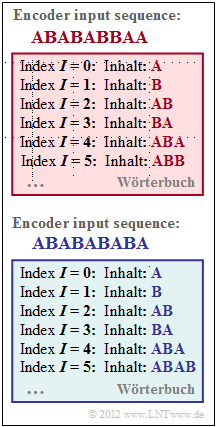
| − | + | The graph shows snapshots of the dictionary created during LZW coding of the input symbol sequence. | |
| − | * | + | *The upper graph is for input symbol sequence <b>ABABABBAA</b>. |
| − | * | + | *The lower dictionary is created during LZW coding of the sequence <b>ABABABABA</b>. |
| − | In | + | In both cases, it is assumed that no characters other than <b>A</b> and <b>B</b> can occur at later times. |
| − | + | In <u>LZW decoding</u>, the same dictionaries are created, but then the dictionary entries occur one step later. In subtask '''(3)''' the question is asked for which coding step or for which decoding step the two snapshots shown are valid. | |
| − | + | In <u>LZW coding</u>, an index $I$ is selected for each coding step $i$ and transmitted (binary). The character pair <b>AB</b> is represented by the index $I = 2$ in the two dictionaries. Here we consider the index $I$ as a decimal number and leave the binary representation out of consideration for this task. | |
| − | + | With <u>LZW decoding</u>, a character or character sequence is generated in the same way from each index $I$ with the help of the dictionary, for example $I = 1$ leads to the character <b>B</b> and $I = 2$ to the character pair <b>AB</b>. | |
| − | + | If a dictionary entry with the desired index $I$ is actually found, the decoding runs smoothly. However, this is not always the case: | |
| − | * | + | * If a new index $I$ is entered during encoding at step $i$ and this $I$ is at the same time the encoding result of the step, this index is not yet occupied in the dictionary at decoding step $i$ . The reason for this is that with the decoder the entries are made one step later than with the coder. |
| − | * | + | * In the case of a binary input sequence $($all characters are <b>A</b> or <b>B</b>$)$ , a special rule must always be applied in LZW decoding if the entry with index $I = i$ was made in coding step $i$ . |
| − | + | This special rule shall be illustrated by an example: | |
| − | * | + | * For step $i$ there is no entry in the decoder dictionary matching index $I$ . |
| − | * | + | * We assume that in the previous step $(i- 1)$ the decoding result was <b>ABBABA</b> . |
| − | * | + | * Then we add the first character of the sequence to this string. Here: <b>ABBABAA</b>. |
| − | * | + | * Then one enters the sequence <b>ABBABAA</b> into the dictionary under index $I$ . |
| Line 44: | Line 44: | ||
:: [[Information_Theory/Komprimierung_nach_Lempel,_Ziv_und_Welch#Decoding_of_the_LZW_algorithm|Decoding of the LZW algorithm]]. | :: [[Information_Theory/Komprimierung_nach_Lempel,_Ziv_und_Welch#Decoding_of_the_LZW_algorithm|Decoding of the LZW algorithm]]. | ||
| − | * | + | *Also, when solving this task, note that the LZW algorithm does not assume an empty dictionary. |
| − | * | + | *Rather, the indices $I = 0$ to $I = M- 1$ contain all $M$ permissible characters of the alphabet. |
| − | + | ===Questions=== | |
| − | === | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Code the input sequence <b>ABABABBAA</b> according to the <u>above diagram</u>. Which indices $I_i$ result for the steps $i=1$, ... , $i=5$? |
|type="{}"} | |type="{}"} | ||
$I_1 \ = \ $ { 0. } | $I_1 \ = \ $ { 0. } | ||
| Line 61: | Line 60: | ||
| − | { | + | {Now code the input sequence <b>ABABABABA</b> according to the <u>diagram below</u>. Specify the indices $I_i$ for the steps $i=4$ and $i=5$ . |
|type="{}"} | |type="{}"} | ||
$I_4 \ = \ $ { 4 } | $I_4 \ = \ $ { 4 } | ||
| Line 67: | Line 66: | ||
| − | { | + | {For which step $i$ does the snapshot of the dictionary shown on the input page apply with respect to |
|type="{}"} | |type="{}"} | ||
| − | $\text{ | + | $\text{Encoding:} \ \ i \ = \ $ { 4 } |
| − | $\text{ | + | $\text{Decoding:} \ \ i \ = \ $ { 5 } |
| − | { | + | {When does one have to resort to the decoding special case rule? |
|type="[]"} | |type="[]"} | ||
| − | - | + | - When decoding <b>ABABABBAA</b> in step $i = 4$. |
| − | + | + | + When decoding <b>ABABABABA</b> in step $i = 4$. |
| − | - | + | - When decoding <b>ABABABABA</b> in step $i = 5$. |
| Line 83: | Line 82: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
'''(1)''' Wir bezeichnen mit $W(I)$ ein Feld (Array), welches das Wörterbuch beschreibt und dessen Elemente Character oder Zeichenfolgen beinhalten. | '''(1)''' Wir bezeichnen mit $W(I)$ ein Feld (Array), welches das Wörterbuch beschreibt und dessen Elemente Character oder Zeichenfolgen beinhalten. | ||
Revision as of 11:58, 15 July 2021
The graph shows snapshots of the dictionary created during LZW coding of the input symbol sequence.
- The upper graph is for input symbol sequence ABABABBAA.
- The lower dictionary is created during LZW coding of the sequence ABABABABA.
In both cases, it is assumed that no characters other than A and B can occur at later times.
In LZW decoding, the same dictionaries are created, but then the dictionary entries occur one step later. In subtask (3) the question is asked for which coding step or for which decoding step the two snapshots shown are valid.
In LZW coding, an index $I$ is selected for each coding step $i$ and transmitted (binary). The character pair AB is represented by the index $I = 2$ in the two dictionaries. Here we consider the index $I$ as a decimal number and leave the binary representation out of consideration for this task.
With LZW decoding, a character or character sequence is generated in the same way from each index $I$ with the help of the dictionary, for example $I = 1$ leads to the character B and $I = 2$ to the character pair AB.
If a dictionary entry with the desired index $I$ is actually found, the decoding runs smoothly. However, this is not always the case:
- If a new index $I$ is entered during encoding at step $i$ and this $I$ is at the same time the encoding result of the step, this index is not yet occupied in the dictionary at decoding step $i$ . The reason for this is that with the decoder the entries are made one step later than with the coder.
- In the case of a binary input sequence $($all characters are A or B$)$ , a special rule must always be applied in LZW decoding if the entry with index $I = i$ was made in coding step $i$ .
This special rule shall be illustrated by an example:
- For step $i$ there is no entry in the decoder dictionary matching index $I$ .
- We assume that in the previous step $(i- 1)$ the decoding result was ABBABA .
- Then we add the first character of the sequence to this string. Here: ABBABAA.
- Then one enters the sequence ABBABAA into the dictionary under index $I$ .
Hints:
- The exercise belongs to the chapter Compression according to Lempel, Ziv and Welch.
- In particular, reference is made to the pages
- Also, when solving this task, note that the LZW algorithm does not assume an empty dictionary.
- Rather, the indices $I = 0$ to $I = M- 1$ contain all $M$ permissible characters of the alphabet.
Questions
Solution
- Die Codierung von ABABABBAA läuft dann wie folgt ab:
- $i = 1$: A → $\underline{I=0}$, $W(I = 2) =$ AB,
- $i = 2$: B → $\underline{I=1}$, $W(I = 3) =$ BA,
- $i = 3$: AB → $\underline{I=2}$, $W(I = 4) =$ ABA,
- $i = 4$: AB → $\underline{I=2}$, $W(I = 5) =$ ABB,
- $i = 5$: BA → $\underline{I=3}$, $W(I = 6) =$ BAA.
- Es ist anzumerken, dass das letzte Zeichen $($A$)$ des Eingabestrings ABABABBAA zum Zeitpunkt $i = 5$ zwar bereits beim Wörterbucheintrag berücksichtigt ist, aber noch nicht codiert wurde.
(2) Für die Schritte $i = 1$ bis $i = 3$ ändert sich nichts gegenüber der Teilaufgabe (1).
- Danach gilt:
- $i = 4$: ABA → $\underline{I=4}$, $W(I = 5) =$ ABAB,
- $i = 5$: BA → $\underline{I=3}$, Codierung abgeschlossen, kein neuer Wörterbucheintrag möglich.
(3) Der Vergleich mit obigen Ergebnissen zeigt:
- Das Wörterbuch des Coders weist genau nach $\underline{i=4}$ Codierschritten die gezeigten Einträge auf.
- Beim Decoder ergibt sich demgegenüber eine Zeitverzögerung um einen Schritt: $\underline{i=5}$.
(4) Richtig ist der Lösungsvorschlag 2:
- Die Sonderfallregelung der Decodierung ist (im vorliegenden Beispiel) dann notwendig, wenn im Codierschritt $i$ der Index $I =i$ ausgegeben wird.
- Bei der Decodierung findet er dann die erforderliche Zuordnung "Index → Zeichenfolge" nicht, da das generierte Wörterbuch zum Zeitpunkt $i$ nur Einträge mit Indizes $I < i$ enthält.
- Für die Folge ABABABBAA gilt entsprechend der Teilaufgabe (1) stets $I < i$.
- Dagegen ergäbe sich für die Folge ABABABABA folgende Indizes:
- $$i = 1\hspace{-0.15cm}: \hspace{0.15cm} I = 0\hspace{0.05cm}, \hspace{0.5cm}i = 2\hspace{-0.15cm}: \hspace{0.15cm}I = 1\hspace{0.05cm}, \hspace{0.5cm}i = 3\hspace{-0.15cm}: \hspace{0.15cm}I = 2\hspace{0.05cm}, \hspace{0.5cm}\underline{i = 4\hspace{-0.15cm}: \hspace{0.15cm}I = 4}\hspace{0.05cm}, \hspace{0.5cm}i = 5\hspace{-0.15cm}: \hspace{0.15cm}I = 3\hspace{0.05cm}. $$
Hier noch zusammenfassend die gesamte Decodierung von ABABABABA:
- Die Vorbelegung des Wörterbuchs beinhaltet $(I=0$: A$)$ und $(I=1$: B$)$.
- Dann gilt mit dem Wörterbuch–Array $W(I)$:
- $i = 1$: Decodierung $I=0$ → A,
- $i = 2$: Decodierung $I=1$ → B, $W(I = 2) =$ AB,
- $i = 3$: Decodierung $I=2$ → AB, $W(I = 3) =$ BA,
- $i = 4$: Ein Eintrag mit dem Index $I = 4$ ist nicht vorhanden ⇒ Sonderfallregelung:
Man nimmt das letzte Decodierergebnis $($hier AB$)$ und fügt das erste Zeichen dieser Sequenz hinten an ⇒ ABA.
Danach wird ABA im Wörterbuch unter dem Index $I = 4$ abgelegt. - $i = 5$: Decodierung $I=3$ → BA. Ende der Decoder–Eingangsfolge.