Aufgaben:Exercise 2.7: Huffman Application for Binary Two-Tuples

• Return to book

Three binary codes for  $M = 4$

The application of the Huffman algorithm in its original form assumes a symbol set  $M > 2$  and is therefore useless for data compression of binary sources.

However, if one combines several consecutive binary characters of the message source into a new symbol, one can usefully apply Huffman data compression to the new symbol set.

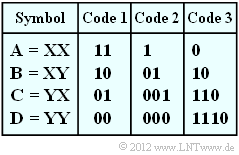
In this task we start from the symbol set  $\{$ $\rm X$,  $\rm Y$ $\}$  ⇒  aus  $(M = 2)$  and form two-tuples according to the table above with the symbol set  $\{$ $\rm A$,  $\rm B$,  $\rm C$,  $\rm D$ $\}$  ⇒  $(M\hspace{0.03cm}' = M^2 = 4)$. 

For example, the binary source symbol sequence  $\rm XYXXYXXXYY$  thus becomes the quaternary sequence  $\rm BACAD$.

Furthermore, three codes are given in the above table, some of which have been created by the Huffman algorithm. The binary output sequences then result for our example as follows:

• $\text{Code 1}$:   1011011100,
• $\text{Code 2}$:   0110011000,
• $\text{Code 3}$:   10011001110.

Again for understanding:

• From the original symbol set  $\{$ $\rm X$,  $\rm Y$ $\}$  a quaternary set with symbol set  $\{$ $\rm A$,  $\rm B$,  $\rm C$,  $\rm D$ $\}$ is obtained by forming two-tuples. 
• The sequence length $N$ is thereby halved to  $N\hspace{0.03cm}' = N/2 $ .
• Huffman coding again results in a binary sequence whose symbol set is designated  $\{$0,  1$\}$  for better differentiation.
• The application of Huffman coding makes sense exactly when the length  $L$  of the initial sequence is smaller than  $N$ (on statistical average).

This task is intended to clarify which of the given binary codes make sense under which boundary conditions.

• Let the binary message source  $\{$ $\rm X$,  $\rm Y$ $\}$  be memoryless and be described solely by the symbol probability  $p_{\rm X}$ .
• The second probability is then always  $p_{\rm Y} = 1 - p_{\rm X}$.

Hints:

• The task belongs to the chapter  Entropy Coding according to Huffman.
• In particular, reference is made to the page  Application of Huffman coding to  $k$-tuples  Bezug genommen.
• The mean codeword length per two-tuple is  $L_{\rm M}\hspace{0.03cm}' = p_{\rm A} \cdot L_{\rm A} +$  ...  $ + p_{\rm D} \cdot L_{\rm D} \hspace{0.05cm}$.  With respect to a source symbol,  $L_{\rm M} = L_{\rm M}\hspace{0.03cm}'/2$.
• A comparable task with ternary input symbols is treated in  Exercise 2.7Z .

• The idea for this task arose during a lecture by  Prof. Robert Fischer  from the University of Ulm at the Technical University of Munich on the topic of "Der goldene Schnitt in der Nachrichtentechnik" (The golden ration in communications technology).

Questions

1

Give the code word lengths with redundancy-free binary source.

$\text{Code 1}$:   $L_{\rm M} \ = \ $ $\ \rm bit/source\:symbol$

$\text{Code 2}$:   $L_{\rm M} \ = \ $ $\ \rm bit/source\:symbol$

$\text{Code 3}$:   $L_{\rm M} \ = \ $ $\ \rm bit/source\:symbol$

2

Determine the Huffman code with respect to two-tuple for  $p_{\rm X}= 0.6$.

	The result is  $\text{Code 1}$.
	The result is  $\text{Code 2}$.
	The result is  $\text{Code 3}$.

3

What is the mean codeword length of the best Huffman code for  $p_{\rm X}= 0.6$ ?

$L_{\rm M} \ = \ $ $\ \rm bit/source\:symbol$

4

Determine the Huffman code with respect to two-tuple for  $p_{\rm X}= 0.8$.

	The result is  $\text{Code 1}$.
	The result is  $\text{Code 2}$.
	The result is  $\text{Code 3}$.

5

What is the mean codeword length of the best Huffman code for  $p_{\rm X}= 0.8$ ?

$L_{\rm M} \ = \ $ $\ \rm bit/source\:symbol$

6

In what range may the probability  $p_{\rm X}$  for the symbol  $\rm X$  lie so that the  $\text{code 1}$  results according to Huffman?

$p_\text{X, min}\ = \ $

$p_\text{X, max}\ = \ $

Solution

Solution

(1)  With redundancy-free binary source  $(p_{\rm X} = p_{\rm Y} = 0.5)$  one obtains  $p_{\rm A} = p_{\rm B} = p_{\rm C} = p_{\rm D} = 0.25$  and with the given equation:

$$L_{\rm M} = \big [ \hspace{0.05cm}p_{\rm A} \cdot L_{\rm A} + p_{\rm B} \cdot L_{\rm B} + p_{\rm C} \cdot L_{\rm C} + p_{\rm D} \cdot L_{\rm D} \hspace{0.05cm} \big ] / 2 = \big [ \hspace{0.05cm} L_{\rm A} + L_{\rm B} + L_{\rm C} + L_{\rm D}\hspace{0.05cm} \big ] / 8 \hspace{0.05cm}.$$

Taking into account the given assignments, we obtain for

• $\text{Code 1}$:    $L_{\rm M} \hspace{0.15cm}\underline{= 1.000 \ {\rm bit/source \:symbol} }$,
• $\text{Code 2}$:    $L_{\rm M} \hspace{0.15cm}\underline{= 1.125 \ {\rm bit/source \:symbol} }$,
• $\text{Code 3}$:    $L_{\rm M} \hspace{0.15cm}\underline{= 1.250 \ {\rm bit/source \:symbol} }$.

In the course of the task it will become apparent that the first two codes are quite possible as a result of the Huffman algorithm (of course only with suitable symbol probabilities).   $\text{Code 3}$  is also prefix-free, but never optimal in terms of mean codeword length.

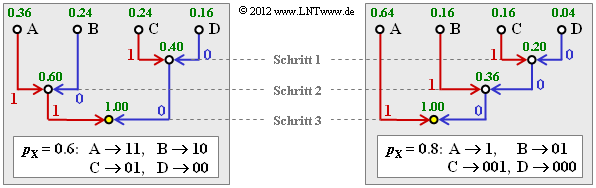
(2)  The probabilities of the possible two-tuples are:

$$p_{\rm A} = 0.6^2 = 0.36 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm B}= 0.6 \cdot 0.4 = 0.24 = p_{\rm C} \hspace{0.05cm},\hspace{0.4cm} p_{\rm D}= 0.4^2 = 0.16 \hspace{0.05cm}.$$

• This gives the  tree diagram on the left  (in the adjacent graph) and the following Huffman code:

Huffman tree diagram for two different two-tuple constellations

    $\rm A$   →   11,   $\rm B$   →   10,   $\rm C$   →   01,   $\rm D$   →   00.

• This is  $\text{Code 1}$   ⇒   solution suggestion 1.

(3)  Each two-tuple is represented by two bits.  Thus

$$L_{\rm M} \hspace{0.15cm}\underline{= 1.000 \ {\rm bit/source \:symbol} }.$$

(4)  Here the probabilities of each two-tuple are:

$$p_{\rm A} = 0.8^2 = 0.64 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm B}= 0.8 \cdot 0.2 = 0.16 \hspace{0.05cm}, $$

$$p_{\rm C} = p_{\rm B}= 0.8 = 0.16 \hspace{0.05cm},\hspace{0.4cm} p_{\rm D}= 0.2^2 = 0.04 \hspace{0.05cm}. $$

According to the tree diagram on the right the result is now  $\text{code 2}$   ⇒   solution suggestion 2:

    $\rm A$   →   1,   $\rm B$   →   01,   $\rm C$   →   001,   $\rm D$   →   010.

(5)  For  $\text{code 2}$  the mean two-tuple length or the mean codeword length is:

$$L_{\rm M}\hspace{0.01cm}' = 0.64 \cdot 1 + 0.16 \cdot 2 + (0.16 + 0.04) \cdot 3 = 1.56\,{\rm bit/two-tuples}\hspace{0.3cm} \Rightarrow\hspace{0.3cm}L_{\rm M} = {L_{\rm M}\hspace{0.01cm}'}/{2}\hspace{0.15cm}\underline{ = 0.78\,{\rm bit/source \:symbol}}\hspace{0.05cm}.$$

(6)  From the earlier subtasks it has been found:

• For  $p_{\rm X} = 0.6$    $\text{code 1}$  is optimal and the mean codeword length of this code is  $($independent of  $p_{\rm X})$  $L_{\rm M} = 1$  bit/source \:symbol.
• For  $p_{\rm X} = 0.8$  according to subtask  (4) ,  $\text{code 2}$  is optimal and the mean codeword length is  $L_{\rm M} = 0.78$  bit/source \:symbol.

The sought maximum value  $p_\text{X, max}$  will thus lie between  $0.6$  and  $0.8$ .  The determining equation here is that for the limiting case  $p_\text{X} = p_\text{X, max}$  both codes have exactly the same mean codeword length  $L_{\rm M} = 1$  bit/source \:symbol besitzen, or  $L_{\rm M}\hspace{0.03cm}' = 2$  bit/two-tuples.

• With the abbreviation  $p = p_\text{X, max}$  max the corresponding determining equation is:

$$L_{\rm M}\hspace{0.01cm}'\hspace{0.15cm}{\rm (Code \hspace{0.15cm}2)} = p^2 \cdot 1 + p \cdot (1-p) \cdot 2 + p \cdot (1-p) \cdot 3 + (1-p)^2 \cdot 3 \stackrel{!}{=} 2 \hspace{0.05cm}.$$

• This leads to the numerical result:

$$p^2 + p - 1 \stackrel{!}{=} 0 \hspace{0.3cm}\Rightarrow\hspace{0.3cm} p_{\rm X,\hspace{0.05cm}max} = p = \frac{\sqrt{5}-1}{2} \hspace{0.15cm}\underline{ \approx 0.618} \hspace{0.05cm}.$$

• Since the basic Huffman structure does not change by swapping  $\rm X$  and  $\rm Y$  the lower bound is:

$$p_{\rm X,\hspace{0.05cm}min} = 1 - p_{\rm X,\hspace{0.05cm}max}\hspace{0.15cm}\underline{ \approx 0.382} \hspace{0.05cm}.$$

The representation of the tuples of two by bit sequences of different lengths  $\text{(code 2)}$  therefore only makes sense if the symbol probabilities of  $\rm X$  and  $\rm Y$  differ significantly.  If, on the other hand, they are between  $0.382$  and  $0.618$,  $\text{code 1}$  is to be applied.

The division of a path of length   $1$  into two sections of length  $0.618$...  and  $0.382$...  is called the  Golden ratio, which is encountered again and again in the most diverse fields.