Exercise 2.13Z: Combination of BWT and MTF

• Return to book

Scheme for Burrows-Wheeler data compression

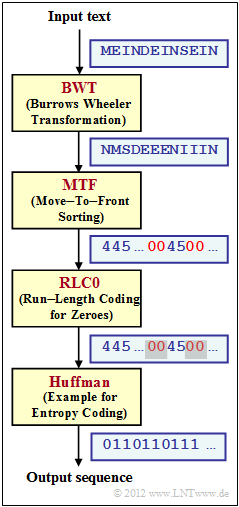
We refer to the theory page  Application Scenario for the Burrows-Wheeler Transform  and consider the coding system sketched on the right, consisting of the blocks.

• Burrows–Wheeler–Transformation  $\rm (BWT)$  as described in  Exercise 2.13; the two character sets at the input and output of the BWT are the same:   $\{$ $\rm D$,  $\rm E$,  $\rm I$,  $\rm M$,  $\rm N$,  $\rm S$ $\}$;
• Move–to–Front  $\rm (MTF)$, a sorting algorithm that outputs a string of the same length  $($  $N = 12 in the example)$, but with a different alphabet  $\{$0,  1,  2,  3,  4,  5$\}$ ;
• $\rm RLC0$  – a run-length encoding specifically for zero, which is (as) frequent according to  $\rm BWT$  and  $\rm MTF$  ;  all other indices are not changed by  $\rm RLC0$ ;
• $\rm Huffman$  as described in the chapter  Entropy coding according to Huffman; frequent characters are represented by short binary sequences and rare ones by long ones.

The  $\rm MTF$–algorithm can be described as follows for  $M = 6$  input symbols:

• The output sequence of the  $\rm MTF$  is a string of indices from the set

       $ I = \{$0,  1,  2,  3,  4,  5$\}$.

• Before starting the actual  $\rm MTF$ algorithm, the possible input symbols are sorted lexicographically and assigned to the following indices:

        $\rm D$   →   0,     $\rm E$   →   1,     $\rm I$   →   2,     $\rm M$   →   3,     $\rm N$   →   4,    $\rm S$   →   5.

• Let the  $\rm MTF$ input string here be  $\rm N\hspace{0.05cm}M\hspace{0.05cm}S\hspace{0.05cm}D\hspace{0.05cm}E\hspace{0.05cm}E\hspace{0.05cm}E\hspace{0.05cm}N\hspace{0.05cm}I\hspace{0.05cm}I\hspace{0.05cm}I\hspace{0.05cm}N$.  This was the  $\rm BWT$ result in  Exercise 2.13.  The first  $\rm N$  is represented as  $I = 4$  according to the default setting.
• Then the  $\rm N$  is placed at the beginning in the sorting, so that after the coding step  $i = 1$  the assignment holds:

        $\rm N$   →   0,     $\rm D$   →   1,     $\rm E$   →   2,     $\rm I$   →   3,     $\rm M$   →   4,    $\rm S$   →   5.

• Continue in the same way until the entire input text has been processed.  If a character is already at position  0, no reordering is necessary.

Hints:

• The exercise belongs to the chapter  Other source coding methods.
• In particular, reference is made to the page  Burrows–Wheeler Transformation.
• Information on the Huffman code can be found in the chapter  Entropy Coding according to Huffman.  This information is not necessary for the solution of the task.

Questions

1

Which statements are true for block  $\rm BWT$  of the coding system?

	The input character set is  $\{ \hspace{0.05cm}\rm D,\hspace{0.05cm} E,\hspace{0.05cm} I,\hspace{0.05cm} M,\hspace{0.05cm} N , \hspace{0.05cm} S \}$.
	The output character set is $\{ \hspace{0.05cm}\rm D,\hspace{0.05cm} E,\hspace{0.05cm} I,\hspace{0.05cm} M,\hspace{0.05cm} N , \hspace{0.05cm} S \}$.
	In the output sequence, allnbsp; $M = 6$  characters occur grouped together.

2

Which statements are true for the block  $\rm MTF$  of the coding system?

	The output character set is  $\{ \hspace{0.05cm}\rm D,\hspace{0.05cm} E,\hspace{0.05cm} I,\hspace{0.05cm} M,\hspace{0.05cm} N , \hspace{0.05cm} S \}$.
	The output character set is  $\{ \hspace{0.05cm}\rm 0,\hspace{0.05cm} 1,\hspace{0.05cm} 2,\hspace{0.05cm} 3,\hspace{0.05cm} 4 , \hspace{0.05cm} 5 \}$.
	The MTF output sequence has length  $N = 12$.

3

What is the  $\rm MTF$ output sequence?

	$\rm 230000100405$,
	$\rm 445340045001$,
	$\rm 543120345123$.

4

Which statements apply to block  $\rm RLC0$  of the coding system?

	The input value  $0$  receives special treatment
	The more often a  $0$  occurs, the more effective this block is.
	The best would be  $\rm Pr(0) ≈ Pr(1) ≈ \text{...} ≈ Pr(5)$.

5

Which statements are true for the final block "Huffman"?

	The initial sequence is binary.
	It causes the smallest possible average codeword length.
	The dimensioning depends on the other blocks.

Solutions

Solution

(1)  The graph on the information page shows that solution suggestions 1 and 2 are correct and suggestion 3 is incorrect:

• $\rm E$  und  $\rm I$  treten zwar gruppiert auf,
• aber nicht die  $\rm N$–Zeichen.

(2) Proposed solutions 2 and 3 are correct:

• The input sequence is processed character by character.  Thus, the output sequence also has the length  $N = 12$.
• In fact, the input set  $\{ \hspace{0.05cm}\rm D,\hspace{0.05cm} E,\hspace{0.05cm} I,\hspace{0.05cm} M,\hspace{0.05cm} N , \hspace{0.05cm} S \}$  in die Ausgangsmenge  $\{ \hspace{0.05cm}\rm 0,\hspace{0.05cm} 1,\hspace{0.05cm} 2,\hspace{0.05cm} 3,\hspace{0.05cm} 4 , \hspace{0.05cm} 5 \}$  is converted into the output set.
• However, not by simple  mapping, but by an algorithm which is outlined below.

Example of the MTF algorithm

(3)  Correct is solution suggestion 2:

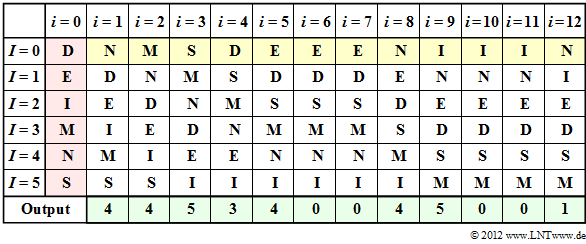
• The table shows the MTF algorithm.  The step  $i=0$  (red background) indicates the preassignment.  The input of the MTF is highlighted in yellow, the output in green.
• In step  $i=1$ , the input character  $\rm N$  corresponding to column  $i=0$  is represented by index  $I = 4$ .  Subsequently,  $\rm N$  is sorted to the front, while the order of the other characters remains the same.
• The input character  $\rm M$  in the second step is also given the index  $I = 4$ according to column  $i=2$ .  One continues in the same way until the twelfth character  $\rm N$, to which the index  $I = 1$  is assigned.
• You can see from the above table that at the times  $i=6$,  $i=7$,  $i=10$  and  $i=11$  the output index is  $I = 0$ .

(4)  Statements 1 and 2 are correct:

• The preprocessings "BWT" and "MTF" only have the task to generate as many zeros as possible.

(5)  All statements are correct.

• You can find more information on the Huffman algorithm in the chapter "Entropy coding according to Huffman".