Aufgaben:Exercise 2.5: Residual Redundancy with LZW Coding

• Return to book

Residual redundancy  $r(N)$  and approximation   $r\hspace{0.05cm}'(N)$  of three sources

We assume here a binary input sequence of length  $N$  and consider three different binary sources:

• $\rm BQ1$:   Symbol probabilities  $p_{\rm A} = 0.89$  and  $p_{\rm B} = 0.11$, i.e. different
    ⇒   entropy   $H = 0.5\text{ bit/source symbol}$   ⇒   the source is redundant.
• $\rm BQ2$:   $p_{\rm A} = p_{\rm B} = 0.5$  (equally probable)
    ⇒   entropy   $H = 1\text{ bit/source symbol}$   ⇒   the source is redundancy-free.
• $\rm BQ3$:   There is no concrete information on the statistics here. 
  In subtask  (6)  you are to estimate the entropy  $H$  of this source.

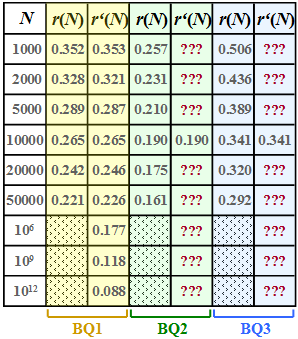
For these three sources, the respective  "residual redundancy"  $r(N)$  was determined by simulation, which remains in the binary sequence after  Lempel–Ziv–Welch coding. 

The results are shown in the first column of the above table for the sources

• $\rm BQ1$  (yellow background),
• $\rm BQ2$  (green background) and
• $\rm BQ3$  (blue background)

whereby we have restricted ourselves to sequence lengths  $N ≤ 50000$  in the simulation.

The  "relative redundancy of the output sequence" – simplified called  "residual redundancy" – can be calculated from

• the length  $N$  of the input sequence,
• the length  $L(N)$  of the output sequence and
• the entropy  $H$

in the following way:

$$r(N) = \frac{L(N) - N \cdot H}{L(N)}= 1 - \frac{ N \cdot H}{L(N)}\hspace{0.05cm}.$$

This takes into account that with perfect source coding the length of the output sequence could be lowered to the value  $L_{\rm min} = N · H$ .

• With non-perfect source coding,  $L(n) - N · H$  gives the remaining redundancy  (with the pseudo–unit  "bit").
• After dividing by  $L(n)$,  one obtains the relative redundancy  $r(n)$  with the value range between zero and one;  $r(n)$  should be as small as possible.

A second parameter for measuring the efficiency of LZW coding is the  "compression factor"  $K(N)$  as the quotient of the lengths of the output and input sequences, which should also be very small:

$$K(N) = {L(N) }/{N} \hspace{0.05cm},$$

In the  theory section  it was shown that the residual redundancy  $r(n)$  is well approximated by the function

$$r\hspace{0.05cm}'(N) =\frac {A}{{\rm lg}\hspace{0.1cm}(N)} \hspace{0.5cm}{\rm mit}\hspace{0.5cm} A = 4 \cdot {r(N = 10000)} \hspace{0.05cm}.$$

• This approximation  $r\hspace{0.05cm}'(N)$  is given for  $\rm BQ1$  in the second column of the table above.
• In subtasks  (4)  and  (5)  you are to make the approximation for sources  $\rm BQ2$  and  $\rm BQ3$ .

Hints:

• The task belongs to the chapter  Compression according to Lempel, Ziv and Welch.
• In particular, reference is made to the pages

Remaining redundancy as a measure for the efficiency of coding methods,

Efficiency of Lempel-Ziv coding and

Quantitative statements on asymptotic optimality.

• The descriptive variables  $K(N)$  and  $r(N)$  are deterministically related.

Questions

1

With which parameter  $A$  was the approximation  $r\hspace{0.05cm}'(N)$  of the residual redundancy for the binary source  $\rm BQ1$  created?

$A \ = \ $

2

What is the minimum size of  $N = N_2$  for  $\rm BQ1$  so that the residual redundancy satisfies the condition  $r(N) ≈ r\hspace{0.05cm}'(N) \le 5\%$ ?

$N_{2} \ = \ $ $\ \cdot 10^{21}$

3

What is the minimum size of  $N = N_3$  at  $\rm BQ1$  so that the compression factor  $K(N)= L(N)/N$  is not greater than  $0.6$?

$N_{3} \ = \ $ $\ \cdot 10^{6}$

4

Now determine the redundancy approximation  $r\hspace{0.05cm}'(N)$  for the redundancy-free binary source $\rm BQ2$, in particular:

$r'(N = 50000)\ = \ $

$r'(N = 10^6)\ = \ $

$r'(N = 10^{12})\ = \ $

5

What values does the redundancy approximation  $r\hspace{0.05cm}'(N)$  yield for the unspecified binary source  $\rm BQ3$? In particular:

$r'(N = 50000)\ = \ $

$r'(N = 10^6)\ = \ $

$r'(N = 10^{12})\ = \ $

6

According to this result, what source entropy  $H$  could  $\rm BQ3$  ?  Hint:  Exactly one answer is correct.

	$H = 1.00 \ \rm bit/source symbol$,
	$H = 0.75 \ \rm bit/source symbol$,
	$H = 0.50 \ \rm bit/source symbol$,
	$H = 0.25 \ \rm bit/source symbol$.

Solution

Solution

(1)  The approximation  $r\hspace{0.05cm}'(N)$  agrees exactly by definition for the sequence length  $N = 10000$  with the residual redundancy  $r(N) = 0.265$  determined by simulation.

• Thus

$$A = 4 \cdot r(N = 10000) =4 \cdot {0.265} \hspace{0.15cm}\underline{= 1.06} \hspace{0.05cm}. $$

(2)  From the relationship  ${A}/{\rm lg}\hspace{0.1cm}(N) ≤ 0.05$    ⇒    ${A}/{\rm lg}\hspace{0.1cm}(N) = 0.05$  it follows:

$${{\rm lg}\hspace{0.1cm}N_{\rm 2}} = \frac{A}{0.05} = 21.2 \hspace{0.3cm}\Rightarrow\hspace{0.3cm} N_{\rm 2} = 10^{21.2} \hspace{0.15cm}\underline{= 1.58 \cdot 10^{21}} \hspace{0.05cm}.$$

(3)  In general,  $r(N) = 1 - {H}/{K(N)} \hspace{0.05cm}.$ 

• $\rm BQ1$  has entropy  $H = 0.5$ bit/symbol. 
• It follows that because  $r(N) ≈ r\hspace{0.05cm}'(N)$  für  $K(N_3) = 0.6$:

$$r(N_{\rm c}) = 1 - \frac{0.5}{0.6} = 0.167 \hspace{0.1cm}\Rightarrow\hspace{0.1cm} {\rm lg}\hspace{0.1cm}N_{\rm 3} = \frac{A}{0.167} = 6.36 \hspace{0.1cm}\Rightarrow\hspace{0.1cm} N_{\rm 3} = 10^{6.36} \hspace{0.15cm}\underline{= 2.29 \cdot 10^{6}} \hspace{0.05cm}.$$

Results for  $\rm BQ2$

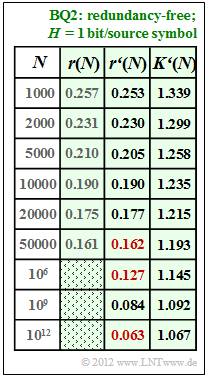
(4)  For  $N = 10000$  gilt  $r(N) ≈ r\hspace{0.05cm}'(N) = 0.19$:

$$\frac{A}{{\rm lg}\hspace{0.1cm}10000} = 0.19 \hspace{0.3cm}\Rightarrow\hspace{0.3cm} A = 0.19 \cdot 4 = 0.76 \hspace{0.05cm}. $$

• The results are summarised in the table opposite.
• One can see the very good agreement between   $r(N)$  and  $r\hspace{0.05cm}'(N)$.
• The numerical values sought are marked in red in the table:

$$r'(N = 50000)\hspace{0.15cm}\underline{ = 0.162},\hspace{0.3cm}r'(N = 10^{6})\hspace{0.15cm}\underline{ = 0.127},\hspace{0.3cm} r'(N = 10^{12})\hspace{0.15cm}\underline{ = 0.063}.$$

• For the compression factor, (the apostrophe indicates that the approximation  $r\hspace{0.05cm}'(N)$  was assumed):

$$K\hspace{0.05cm}'(N) = \frac{1}{1 - r\hspace{0.05cm}'(N)}\hspace{0.05cm}.$$

• Thus, for the length of the LZW output string:

$$L\hspace{0.05cm}'(N) = K\hspace{0.05cm}'(N) \cdot N = \frac{N}{1 - r\hspace{0.05cm}'(N)}\hspace{0.05cm}.$$

Results for  $\rm BQ3$

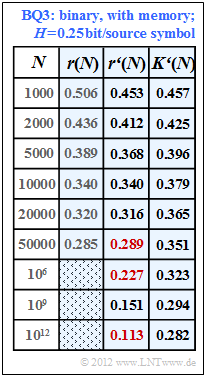
(5)  Following a similar procedure as in subtask  (4)  we obtain the fitting parameter  $\rm BQ3$  for the binary source  $A = 1.36$  and from this the results according to the table with a blue background.

Hint:   The last column of this table is only understandable with knowledge of subtask  (6) . There it is shown that the source  $\rm BQ3$  has the entropy  $H = 0.25$ bit/source symbol.

• In this case, the following applies to the compression factor:

$$K\hspace{0.05cm}'(N) = \frac{H}{1 - r\hspace{0.05cm}'(N)} = \frac{0.25}{1 - r'(N)} \hspace{0.05cm}.$$

• Thus, for the values of residual redundancy we are looking for, we obtain:

$$r\hspace{0.05cm}'(N = 50000)\hspace{0.15cm}\underline{ = 0.289},\hspace{0.3cm}r\hspace{0.05cm}'(N = 10^{6})\hspace{0.15cm}\underline{ = 0.227},\hspace{0.3cm} r\hspace{0.05cm}'(N = 10^{12})\hspace{0.15cm}\underline{ = 0.113}.$$

• Thus, for  $N = 10^{12}$  , the compression factor  $(0.282)$  still deviates significantly from the entropy  $(0.25)$  which can only be achieved for  $N \to \infty$  (source coding theorem).

(6)  The individual approximations  $r\hspace{0.05cm}'(N)$  differ only by the parameter  $A$.  Here we found:

1. Source  $\rm BQ1$  with  $H = 0.50$   ⇒   $A = 1.06$   ⇒   according to the specification sheet,
2. Source  $\rm BQ2$  with  $H = 1.00$   ⇒   $A = 0.76$   ⇒   see subtask  (4),
3. Source  $\rm BQ3$  $(H$ unknown$)$: $A = 4 · 0.34 =1.36$   ⇒   corresponding to the last column in the table.

• Obviously, the smaller the entropy  $H$  the larger the adjustment factor  $A$  (and vice versa).
• Since exactly one solution is possible,   $H = 0.25$  bit/source symbol must be correct   ⇒   answer 4.

• In fact, the probabilities $p_{\rm A} = 0.96$  and  $p_{\rm B} = 0.04$    ⇒   $H ≈ 0.25$ were used in the simulation for source  $\rm BQ3$ .