Difference between revisions of "Aufgaben:Exercise 2.6: About the Huffman Coding"
| Line 93: | Line 93: | ||
| − | {What is the | + | {What is the average codeword length? |
|type="{}"} | |type="{}"} | ||
$L_{\rm M} \ = \ $ { 2.73 3% } $\ \rm bit/source \hspace{0.15cm} symbol$ | $L_{\rm M} \ = \ $ { 2.73 3% } $\ \rm bit/source \hspace{0.15cm} symbol$ | ||
| Line 114: | Line 114: | ||
*By comparison with the data sheet, one obtains: | *By comparison with the data sheet, one obtains: | ||
| − | :Symbol $\rm A$: <u> | + | :Symbol $\rm A$: <u>Input 7</u>, Symbol $\rm B$: <u>Input 6</u>, Symbol $\rm C$: <u>Input 3</u>, Symbol $\rm D$: <u>Input 1</u>. |
[[File:EN_Inf_Z_2_6b.png|right|right|frame|Tree diagram adapted to the exercise]] | [[File:EN_Inf_Z_2_6b.png|right|right|frame|Tree diagram adapted to the exercise]] | ||
| − | |||
| − | + | '''(2)''' The node $\rm R$ is the tree ("root"). This is always assigned $\underline{R=1}$, regardless of the occurrence probabilities. | |
| − | '''(2)''' The node $\rm R$ is the tree ( | ||
The following applies to the other values: | The following applies to the other values: | ||
| Line 135: | Line 133: | ||
:Step 5: $p_{\rm Y} = p_{\rm W} + p_{\rm E} = 0.22 + 0.24 \hspace{0.15cm}\underline{ =0.46}$, | :Step 5: $p_{\rm Y} = p_{\rm W} + p_{\rm E} = 0.22 + 0.24 \hspace{0.15cm}\underline{ =0.46}$, | ||
| − | : | + | :Step 6: $p_{\rm Z} = p_{\rm X} + p_{\rm D} = 0.29 + 0.25 \hspace{0.15cm}\underline{ =0.54}$. |
<br clear=all> | <br clear=all> | ||
| − | '''(3)''' The Huffman code for symbol $\rm A$ is obtained by tracing the path from | + | '''(3)''' The Huffman code for symbol $\rm A$ is obtained by tracing the path from $\rm root$ (yellow dot) to symbol $\rm A$ and assigning a <b>1</b> to each red line and a <b>0</b> to each blue one. |
* Symbol $\rm A$: red–red–red–blue–red→ <b><u>11101</u></b>, | * Symbol $\rm A$: red–red–red–blue–red→ <b><u>11101</u></b>, | ||
| Line 158: | Line 156: | ||
'''(4)''' The coding under point '''(3)''' has shown that | '''(4)''' The coding under point '''(3)''' has shown that | ||
| − | * the symbols $\rm D$ and $\rm E$ with two bits, | + | * the symbols $\rm D$ and $\rm E$ are each represented with two bits, |
* the symbols $\rm C$, $\rm F$ and $\rm G$ with three bits, | * the symbols $\rm C$, $\rm F$ and $\rm G$ with three bits, | ||
| Line 164: | Line 162: | ||
* the symbols $\rm B$ with four bits, and | * the symbols $\rm B$ with four bits, and | ||
| − | * the symbols $\rm A$ and $\rm H$ | + | * the symbols $\rm A$ and $\rm H$ with five bits. |
| − | + | Thus, for the average codeword length (in "bit/source symbol"): | |
:$$L_{\rm M} \hspace{0.2cm} = \hspace{0.2cm} (p_{\rm D} + p_{\rm E}) \cdot 2 + (p_{\rm C} + p_{\rm F} + p_{\rm G}) \cdot 3 + p_{\rm B} \cdot 4 +(p_{\rm A} + p_{\rm H}) \cdot 5 = 0.49 \cdot 2 + 0.36 \cdot 3 +0.08 \cdot 4 +0.07 \cdot 5 | :$$L_{\rm M} \hspace{0.2cm} = \hspace{0.2cm} (p_{\rm D} + p_{\rm E}) \cdot 2 + (p_{\rm C} + p_{\rm F} + p_{\rm G}) \cdot 3 + p_{\rm B} \cdot 4 +(p_{\rm A} + p_{\rm H}) \cdot 5 = 0.49 \cdot 2 + 0.36 \cdot 3 +0.08 \cdot 4 +0.07 \cdot 5 | ||
\hspace{0.15cm}\underline{= 2.73}\hspace{0.05cm}.$$ | \hspace{0.15cm}\underline{= 2.73}\hspace{0.05cm}.$$ | ||
| Line 174: | Line 172: | ||
'''(5)''' Only <u>answer 1</u> is correct: | '''(5)''' Only <u>answer 1</u> is correct: | ||
| − | *The | + | *The average codeword length $L_{\rm M}$ cannot be smaller than the source entropy $H$. This eliminates answers 2 and 3. |
*From the given probabilities of occurrence, the source entropy can actually be calculated to $H = 2.71$ bit/source symbol. | *From the given probabilities of occurrence, the source entropy can actually be calculated to $H = 2.71$ bit/source symbol. | ||
| − | *It can be seen that this Huffman coding almost reaches the given | + | *It can be seen that this Huffman coding almost reaches the given limit ("Source Coding Theorem") $L_{\rm M, \ min } \ge H = 2.71$ bit/source symbol. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Revision as of 15:05, 10 August 2021
We consider here a source symbol sequence $\langle q_\nu \rangle$ with symbol set size $M = 8$:
- $$q_{\nu} \in \{ \hspace{0.05cm}q_{\mu} \} = \{ \boldsymbol{\rm A} \hspace{0.05cm},\hspace{0.05cm} \boldsymbol{\rm B}\hspace{0.05cm},\hspace{0.05cm} \boldsymbol{\rm C}\hspace{0.05cm},\hspace{0.05cm} \boldsymbol{\rm D}\hspace{0.05cm},\hspace{0.05cm} \boldsymbol{\rm E}\hspace{0.05cm},\hspace{0.05cm} \boldsymbol{\rm F}\hspace{0.05cm},\hspace{0.05cm} \boldsymbol{\rm G}\hspace{0.05cm},\hspace{0.05cm} \boldsymbol{\rm H}\hspace{0.05cm} \}\hspace{0.05cm}.$$
If the symbols are equally probable, i.e. $p_{\rm A} = p_{\rm B} =$ ... $ = p_{\rm H} = 1/M$ then source coding makes no sense. Already with the dual code $\rm A$ → 000, $\rm B$ → 001, ... , $\rm H$ → 111, the average codeword length $L_{\rm M}$ is its lower bound $H$ according to the source coding theorem $(H$ denotes the "source entropy" here$)$:
- $$L_{\rm M,\hspace{0.08cm}min} = H = 3 \hspace{0.15cm}{\rm bit/source \:symbol} \hspace{0.05cm}.$$
However, let the symbol probabilities be given as follows:
- $$p_{\rm A} \hspace{-0.05cm}= \hspace{-0.05cm} 0.04 \hspace{0.05cm},\hspace{0.1cm}p_{\rm B} \hspace{-0.05cm}= \hspace{-0.05cm} 0.08 \hspace{0.05cm},\hspace{0.1cm}p_{\rm C} \hspace{-0.05cm}= \hspace{-0.05cm} 0.14 \hspace{0.05cm},\hspace{0.1cm} p_{\rm D} \hspace{-0.05cm}= \hspace{-0.05cm} 0.25 \hspace{0.05cm},\hspace{0.1cm} p_{\rm E} \hspace{-0.05cm}= \hspace{-0.05cm} 0.24 \hspace{0.05cm},\hspace{0.1cm}p_{\rm F} \hspace{-0.05cm}= \hspace{-0.05cm} 0.12 \hspace{0.05cm},\hspace{0.1cm}p_{\rm G} \hspace{-0.05cm}= \hspace{-0.05cm} 0.10 \hspace{0.05cm},\hspace{0.1cm} p_{\rm H} \hspace{-0.05cm}= \hspace{-0.05cm} 0.03 \hspace{0.05cm}.$$
- So here we have a redundant source that can be compressed by Huffman coding.
- This algorithm was published by David Albert Huffman – shortly after Shannon's groundbreaking work on information theory – and allows the construction of optimal prefix-free codes.
The algorithm is given here without derivation and proof, whereby we restrict ourselves to binary codes ⇒ the code symbol sequence consists only of zeros and ones:
- (1) Order the symbols according to decreasing probabilities of occurrence.
- (2) Combine the two least likely symbols into a new symbol.
- (3) Repeat steps (1) and (2), until only two (combined) symbols remain.
- (4) Binary encode the more probable set of symbols with 1 , the other set with 0.
- (5) Step by step (from bottom to top) add 1 or 0 to the split partial codes.
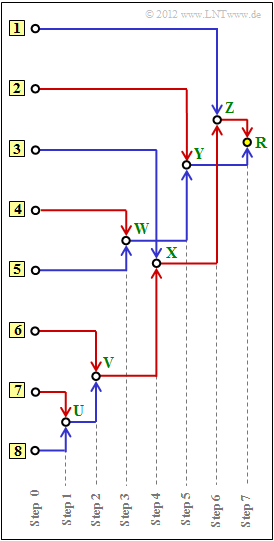
This algorithm is often illustrated by a tree diagram. The diagram above shows this for the case at hand.
You have the following tasks:
- (a) Assign the symbols $\rm A$, ... , $\rm H$ to the inputs labelled [1], ... , [8] .
- (b) Determination of the sum probabilities $U$, ... , $Z$ and $R$ ("root").
- (c) Assignment of the symbols $\rm A$, ... , $\rm H$ to the corresponding Huffman binary sequences. A red connection corresponds to a 1, a blue connection to a 0.
You will notice that the average codeword length for Huffman coding,
- $$L_{\rm M} = \sum_{\mu = 1}^{M}\hspace{0.05cm} p_{\mu} \cdot L_{\mu}, $$
is only slightly larger than the source entropy $H$. In this equation, the following values apply to the present case:
- $M = 8$, $p_1 = p_{\rm A}$, ... , $p_8 = p_{\rm H}$.
- The respective number of bits of the code symbols for $\rm A$, ... , $\rm H$ is denoted by $L_1$, ... , $L_8$ .
Hints:
- The exercise belongs to the chapter Entropy Coding according to Huffman.
- In particular, reference is made to the pages
- To check your results, please refer to the (German language) SWF module Coding according to Huffman and Shannon/Fano.
Questions
Solution
- Since the two least likely symbols are already combined in the first step, the probabilities of occurrence decrease from top to bottom
(from left to right in the diagram for this sample solution). - By comparison with the data sheet, one obtains:
- Symbol $\rm A$: Input 7, Symbol $\rm B$: Input 6, Symbol $\rm C$: Input 3, Symbol $\rm D$: Input 1.
(2) The node $\rm R$ is the tree ("root"). This is always assigned $\underline{R=1}$, regardless of the occurrence probabilities.
The following applies to the other values:
- Step 1: $p_{\rm U} = p_{\rm A} + p_{\rm H} = 0.04 + 0.03 \hspace{0.15cm}\underline{ =0.07}$,
- Step 2: $p_{\rm V} = p_{\rm U} + p_{\rm B} = 0.07 + 0.08 \hspace{0.15cm}\underline{ =0.15}$,
- Step 3: $p_{\rm W} = p_{\rm F} + p_{\rm G} = 0.12 + 0.10 \hspace{0.15cm}\underline{ =0.22}$,
- Step 4: $p_{\rm X} = p_{\rm V} + p_{\rm C} = 0.15 + 0.14 \hspace{0.15cm}\underline{ =0.29}$,
- Step 5: $p_{\rm Y} = p_{\rm W} + p_{\rm E} = 0.22 + 0.24 \hspace{0.15cm}\underline{ =0.46}$,
- Step 6: $p_{\rm Z} = p_{\rm X} + p_{\rm D} = 0.29 + 0.25 \hspace{0.15cm}\underline{ =0.54}$.
(3) The Huffman code for symbol $\rm A$ is obtained by tracing the path from $\rm root$ (yellow dot) to symbol $\rm A$ and assigning a 1 to each red line and a 0 to each blue one.
- Symbol $\rm A$: red–red–red–blue–red→ 11101,
- Symbol $\rm B$: red–red–red–red → 1111,
- Symbol $\rm C$: red–red–blue → 110,
- Symbol $\rm D$: red–blue– → 10,
- Symbol $\rm E$: blue–red → 01,
- Symbol $\rm F$: blue–blue–red → 001,
- Symbol $\rm G$: blue–blue–blue → 000,
- Symbol $\rm H$: red–red–red–blue–blue → 11100.
(4) The coding under point (3) has shown that
- the symbols $\rm D$ and $\rm E$ are each represented with two bits,
- the symbols $\rm C$, $\rm F$ and $\rm G$ with three bits,
- the symbols $\rm B$ with four bits, and
- the symbols $\rm A$ and $\rm H$ with five bits.
Thus, for the average codeword length (in "bit/source symbol"):
- $$L_{\rm M} \hspace{0.2cm} = \hspace{0.2cm} (p_{\rm D} + p_{\rm E}) \cdot 2 + (p_{\rm C} + p_{\rm F} + p_{\rm G}) \cdot 3 + p_{\rm B} \cdot 4 +(p_{\rm A} + p_{\rm H}) \cdot 5 = 0.49 \cdot 2 + 0.36 \cdot 3 +0.08 \cdot 4 +0.07 \cdot 5 \hspace{0.15cm}\underline{= 2.73}\hspace{0.05cm}.$$
(5) Only answer 1 is correct:
- The average codeword length $L_{\rm M}$ cannot be smaller than the source entropy $H$. This eliminates answers 2 and 3.
- From the given probabilities of occurrence, the source entropy can actually be calculated to $H = 2.71$ bit/source symbol.
- It can be seen that this Huffman coding almost reaches the given limit ("Source Coding Theorem") $L_{\rm M, \ min } \ge H = 2.71$ bit/source symbol.