Difference between revisions of "Aufgaben:Exercise 2.10: Shannon-Fano Coding"
| Line 4: | Line 4: | ||
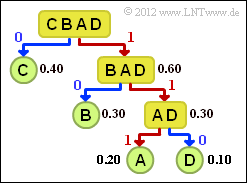
[[File:P_ID2465__Inf_A_2_10.png |right|frame|Tree diagram of the <br>Shannon-Fano coding]] | [[File:P_ID2465__Inf_A_2_10.png |right|frame|Tree diagram of the <br>Shannon-Fano coding]] | ||
| − | Another algorithm for entropy coding was given in 1949 by [https://en.wikipedia.org/wiki/Claude_Shannon Claude Elwood Shannon] and [https://en.wikipedia.org/wiki/Robert_Fano Robert Fano] | + | Another algorithm for entropy coding was given in 1949 by [https://en.wikipedia.org/wiki/Claude_Shannon Claude Elwood Shannon] and [https://en.wikipedia.org/wiki/Robert_Fano Robert Fano], which is described in the theory section. |
| − | This special type of source coding will be described here using a simple example for the symbol | + | This special type of source coding will be described here using a simple example for the symbol set size $M = 4$ and the following symbol probabilities: |
:$$p_{\rm A} = 0.2 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm B}= 0.3 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm C}= 0.4 \hspace{0.05cm},\hspace{0.4cm} | :$$p_{\rm A} = 0.2 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm B}= 0.3 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm C}= 0.4 \hspace{0.05cm},\hspace{0.4cm} | ||
| Line 17: | Line 17: | ||
:2. Divide the symbols into two groups of approximately equal probability, here $\rm C$ and $\rm BAD$. | :2. Divide the symbols into two groups of approximately equal probability, here $\rm C$ and $\rm BAD$. | ||
| − | :3. The binary symbol <b>0</b>is assigned to the less probable group, <b>1</b> to the other group. | + | :3. The binary symbol <b>0</b> is assigned to the less probable group, <b>1</b> to the other group. |
:4. If there is more than one symbol in a group, the algorithm is to be applied recursively. | :4. If there is more than one symbol in a group, the algorithm is to be applied recursively. | ||
| − | For this example, the following code assignment results (in the tree diagram, a red connection marks a <b>1</b> and a blue one a <b>0</b>: | + | For this example, the following code assignment results (in the tree diagram, a red connection marks a <b>1</b> and a blue one a <b>0</b>): |
: $\rm A$ → <b>111</b>, $\rm B$ → <b>10</b>, $\rm C$ → <b>0</b>, $\rm D$ → <b>110</b>. | : $\rm A$ → <b>111</b>, $\rm B$ → <b>10</b>, $\rm C$ → <b>0</b>, $\rm D$ → <b>110</b>. | ||
| − | This gives the following for the | + | This gives the following for the average codeword length: |
| − | :$$L_{\rm M} = 0.4 \cdot 1 + 0.3 \cdot 2 + (0.2 + 0.1) \cdot 3 = 1.9\,\,{\rm bit/source\ | + | :$$L_{\rm M} = 0.4 \cdot 1 + 0.3 \cdot 2 + (0.2 + 0.1) \cdot 3 = 1.9\,\,{\rm bit/source\hspace{0.15cm}symbol}\hspace{0.05cm}.$$ |
The Huffman algorithm would produce a slightly different code here, but even in this case | The Huffman algorithm would produce a slightly different code here, but even in this case | ||
| − | *$\rm C$ is | + | *$\rm C$ is encoded with one bit, |
*$\rm B$ with two bits and | *$\rm B$ with two bits and | ||
*$\rm A$ and $\rm D$ with three bits each. | *$\rm A$ and $\rm D$ with three bits each. | ||
| − | This would also result in $L_{\rm M} = 1.9 \ \rm bit/source\ | + | This would also result in $L_{\rm M} = 1.9 \ \rm bit/source\hspace{0.15cm}symbol$. |
In this task you are to calculate the Shannon-Fano code for $M = 8$ and the probabilities | In this task you are to calculate the Shannon-Fano code for $M = 8$ and the probabilities | ||
:$$p_{\rm A} = 0.10 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm B}= 0.40 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm C}= 0.02 \hspace{0.05cm},\hspace{0.4cm} p_{\rm D}= 0.14 \hspace{0.05cm},\hspace{0.4cm} | :$$p_{\rm A} = 0.10 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm B}= 0.40 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm C}= 0.02 \hspace{0.05cm},\hspace{0.4cm} p_{\rm D}= 0.14 \hspace{0.05cm},\hspace{0.4cm} | ||
| − | p_{\rm E} = 0.17 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm F}= 0.03 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm G}= 0.05 \hspace{0.05cm},\hspace{0.4cm}p_{\rm H}= 0.09$$ | + | p_{\rm E} = 0.17 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm F}= 0.03 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm G}= 0.05 \hspace{0.05cm},\hspace{0.4cm}p_{\rm H}= 0.09.$$ |
| − | + | You will see that with these probabilities "Shannon-Fano" will also differ from "Huffman" in terms of efficiency. | |
With the Huffman code, the following assignment results with the probabilities at hand: | With the Huffman code, the following assignment results with the probabilities at hand: | ||
| Line 57: | Line 57: | ||
*The assignment belongs to the chapter [[Information_Theory/Weitere_Quellencodierverfahren|Other source coding methods]]. | *The assignment belongs to the chapter [[Information_Theory/Weitere_Quellencodierverfahren|Other source coding methods]]. | ||
*In particular, reference is made to the page [[Information_Theory/Weitere_Quellencodierverfahren#The_Shannon-Fano_algorithm|The Shannon-Fano algorithm]]. | *In particular, reference is made to the page [[Information_Theory/Weitere_Quellencodierverfahren#The_Shannon-Fano_algorithm|The Shannon-Fano algorithm]]. | ||
| − | *To check your results, please refer to the | + | *To check your results, please refer to the (German language) SWF module [[Applets:Huffman_Shannon_Fano|Coding according to Huffman and Shannon/Fano]]. |
| Line 65: | Line 65: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {What is the | + | {What is the average codeword length $L_{\rm M}$ for the <u>Huffman code</u>? |
|type="{}"} | |type="{}"} | ||
| − | $L_{\rm M}\ = \ $ { 2.54 3% } $\ \rm bit/source\ | + | $L_{\rm M}\ = \ $ { 2.54 3% } $\ \rm bit/source\hspace{0.15cm}symbol$ |
| Line 86: | Line 86: | ||
{What is the average codeword length $L_{\rm M}$ for <u>Shannon–Fano code</u>? | {What is the average codeword length $L_{\rm M}$ for <u>Shannon–Fano code</u>? | ||
|type="{}"} | |type="{}"} | ||
| − | $L_{\rm M}\ = \ $ { 2.58 3% } $\ \rm bit/source\ | + | $L_{\rm M}\ = \ $ { 2.58 3% } $\ \rm bit/source\hspace{0.15cm}symbol$ |
Revision as of 13:09, 12 August 2021
Another algorithm for entropy coding was given in 1949 by Claude Elwood Shannon and Robert Fano, which is described in the theory section.
This special type of source coding will be described here using a simple example for the symbol set size $M = 4$ and the following symbol probabilities:
- $$p_{\rm A} = 0.2 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm B}= 0.3 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm C}= 0.4 \hspace{0.05cm},\hspace{0.4cm} p_{\rm D}= 0.1 \hspace{0.05cm}. $$
The graph shows the corresponding tree diagram. Proceed as follows:
- 1. Order the symbols according to decreasing probability of occurrence, here $\rm C$ – $\rm B$ – $\rm A$ – $\rm D$.
- 2. Divide the symbols into two groups of approximately equal probability, here $\rm C$ and $\rm BAD$.
- 3. The binary symbol 0 is assigned to the less probable group, 1 to the other group.
- 4. If there is more than one symbol in a group, the algorithm is to be applied recursively.
For this example, the following code assignment results (in the tree diagram, a red connection marks a 1 and a blue one a 0):
- $\rm A$ → 111, $\rm B$ → 10, $\rm C$ → 0, $\rm D$ → 110.
This gives the following for the average codeword length:
- $$L_{\rm M} = 0.4 \cdot 1 + 0.3 \cdot 2 + (0.2 + 0.1) \cdot 3 = 1.9\,\,{\rm bit/source\hspace{0.15cm}symbol}\hspace{0.05cm}.$$
The Huffman algorithm would produce a slightly different code here, but even in this case
- $\rm C$ is encoded with one bit,
- $\rm B$ with two bits and
- $\rm A$ and $\rm D$ with three bits each.
This would also result in $L_{\rm M} = 1.9 \ \rm bit/source\hspace{0.15cm}symbol$.
In this task you are to calculate the Shannon-Fano code for $M = 8$ and the probabilities
- $$p_{\rm A} = 0.10 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm B}= 0.40 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm C}= 0.02 \hspace{0.05cm},\hspace{0.4cm} p_{\rm D}= 0.14 \hspace{0.05cm},\hspace{0.4cm} p_{\rm E} = 0.17 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm F}= 0.03 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm G}= 0.05 \hspace{0.05cm},\hspace{0.4cm}p_{\rm H}= 0.09.$$
You will see that with these probabilities "Shannon-Fano" will also differ from "Huffman" in terms of efficiency.
With the Huffman code, the following assignment results with the probabilities at hand:
- $\rm A$ → 100, $\rm B$ → 0, $\rm C$ → 111100, $\rm D$ → 101, $\rm E$ → 110, $\rm F$ → 111101, $\rm G$ → 11111, $\rm H$ → 1110.
Hints:
- The assignment belongs to the chapter Other source coding methods.
- In particular, reference is made to the page The Shannon-Fano algorithm.
- To check your results, please refer to the (German language) SWF module Coding according to Huffman and Shannon/Fano.
Questions
Solution
- $$L_{\rm M} = 0.4 \cdot 1 + (0.17 + 0.14 + 0.10) \cdot 3 + 0.09 \cdot 4 + 0.05 \cdot 5 + (0.03 + 0.02) \cdot 6 =\underline{ 2.54 \,\,{\rm bit/source\:symbol}}\hspace{0.05cm}. $$
(2) The correct answer is 2:
- Before applying the Shannon-Fano algorithm, the characters must first be sorted according to their occurrence probabilities. Thus, answer 1 is incorrect.
- All sorted characters must be divided into two groups in such a way that the group probabilities are as equal as possible. For the first step:
- $${\rm Pr}(\boldsymbol{\rm BE}) = 0.57\hspace{0.05cm}, \hspace{0.2cm}{\rm Pr}(\boldsymbol{\rm DAHGFC}) = 0.43 \hspace{0.05cm}.$$
- With the distribution according to solution suggestion 3, the equal distribution would be achieved even less:
- $${\rm Pr}(\boldsymbol{\rm B}) = 0.40\hspace{0.05cm}, \hspace{0.2cm}{\rm Pr}(\boldsymbol{\rm EDAHGFC}) = 0.60 \hspace{0.05cm}.$$
(3) All suggeted solutionss are correct:
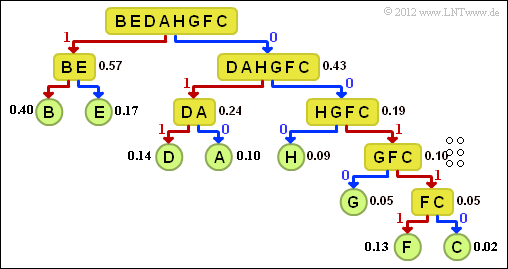
- The graph shows the tree diagram of the Shannon-Fano coding.
- This results in the following assignment (a red connection indicates a 1 , a blue one indicates a 0):
- $\underline{\rm A}$ → 010, $\underline{\rm B}$ → 11, $\underline{\rm C}$ → 00110,
- ${\rm D}$ → 011, ${\rm E}$ → 10, ${\rm F}$ → 00111, ${\rm G}$ → 0010, ${\rm H}$ → 000.
(4) Using the result of sub-task (3) , we get:
- $$L_{\rm M}= (0.40 + 0.17) \cdot 2 + (0.14 + 0.10 + 0.09) \cdot 3 + 0.05 \cdot 4 + (0.03 + 0.02) \cdot 5 =\underline{ 2.58 \,\,{\rm bit/source\:symbol}}\hspace{0.05cm}. $$
(5) Statements 2 and 3 are correct:
- In the present example, Shannon-Fano results in a less favourable value than Huffman.
- In most cases – including the example on the information page – Huffman and Shannon-Fano result in an equivalent code and thus also the same average code word length.
- Shannon-Fano, on the other hand, never delivers a more effective code than Huffman.