Difference between revisions of "Exercise 2.12: Run–Length Coding and Run–Length Limited Coding"
| Line 85: | Line 85: | ||
===Solution=== | ===Solution=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' The binary sequence consists of $N = 1250$ binary symbols (can be read from the last column in the table). This means that the same number of bits is needed without coding: | + | '''(1)''' The binary sequence consists of $N = 1250$ binary symbols (can be read from the last column in the table). |
| − | :$$N_\text{ | + | *This means that the same number of bits is needed without coding: |
| + | :$$N_\text{bits}\hspace{0.15cm}\underline{= 1250}.$$ | ||
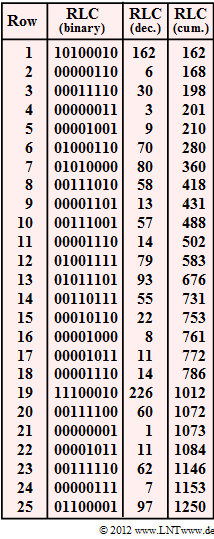
'''(2)''' The entire symbol sequence of length $N = 1250$ contains $N_{\rm B} = 25$ symbols ${\rm B}$ and thus $N_{\rm A} = 1225$ symbols ${\rm A}$. | '''(2)''' The entire symbol sequence of length $N = 1250$ contains $N_{\rm B} = 25$ symbols ${\rm B}$ and thus $N_{\rm A} = 1225$ symbols ${\rm A}$. | ||
| − | *The number $N_{\rm B}$ | + | *The number $N_{\rm B}$ of symbols ${\rm B}$ is equal to the number of rows in the table given at the front. |
| − | *Thus the following applies to the relative frequency of | + | *Thus the following applies to the relative frequency of symbol ${\rm B}$: |
:$$h_{\rm B} = \frac{N_{\rm B}}{N} = \frac{25}{1250} \hspace{0.15cm}\underline{= 0.02} = 2\%\hspace{0.05cm}. $$ | :$$h_{\rm B} = \frac{N_{\rm B}}{N} = \frac{25}{1250} \hspace{0.15cm}\underline{= 0.02} = 2\%\hspace{0.05cm}. $$ | ||
| − | '''(3)''' We now consider | + | '''(3)''' We now consider "Run–Length Coding" $\rm (RLC)$, where each distance between two ${\rm B}$–symbols is represented by eight bits $(D = 8)$. |
| − | *Thus, with $N_{\rm B} = 25$, we get | + | *Thus, with $N_{\rm B} = 25$, we get: |
| − | :$$N_{\rm | + | :$$N_{\rm bits} = N_{\rm B} \cdot 8 \hspace{0.15cm}\underline{= 200} \hspace{0.05cm}.$$ |
| − | '''(4)''' $\rm RLC$ with $D = 7$ only allows values between $1$ und $2^7-1 =127$ for $L_i$ | + | '''(4)''' $\rm RLC$ with $D = 7$ only allows values between $1$ und $2^7-1 =127$ for $L_i$. |
| − | *However, the entry "226" in line 19 is greater ⇒ <u>NO</u>. | + | *However, the entry "226" in line 19 is greater ⇒ <u>NO</u>. |
| − | '''(5)''' Even with Run–Length Limited Coding $\rm (RLLC)$ | + | '''(5)''' Even with Run–Length Limited Coding $\rm (RLLC)$, only values up to $127$ are permitted for the "real" distances $L_i$ with $D = 7$. |
| − | *The entry "226" in line 19 is replaced by the following for $\rm RLLC$ | + | *The entry "226" in line 19 is replaced by the following for $\rm RLLC$: |
| − | :* Line 19a: <b>S</b> = <b>0000000</b> ⇒ special character, stands for "+ 127", | + | :* Line 19a: <b>S</b> = <b>0000000</b> ⇒ special character, stands for "+127", |
:* Line 19b: <b>1100011</b> ⇒ decimal 99. | :* Line 19b: <b>1100011</b> ⇒ decimal 99. | ||
*This gives a total of $26$ words of seven bits each: | *This gives a total of $26$ words of seven bits each: | ||
| − | :$$N_{\rm | + | :$$N_{\rm bits} = 26 \cdot 7 \hspace{0.15cm}\underline{= 182} \hspace{0.05cm}.$$ |
| − | '''(6)''' | + | '''(6)''' With $D = 6$ the following changes have to be made in $\rm RLLC$ compared to $\rm RLC$ (see table): |
| − | * | + | * Line 1: $122 = 1 · 63 + 59$ (one word more), |
| − | * | + | * Line 6: $70 = 1 · 63 + 7$ (one word more), |
| − | * | + | * Line 7: $80 = 1 · 63 + 17$ (one word more), |
| − | * | + | * Line 12: $79 = 1 · 63 + 16$ (one word more), |
| − | * | + | * Line 13: $93 = 1 · 63 + 30$ (one word more), |
| − | * | + | * Line 19: $226 = 3 · 63 + 37$ (one word more), |
| − | * | + | * Line 25: $97 = 1 · 63 + 34$ (one word more). |
| − | This gives a total of $34$ words of six bits each: | + | This gives a total of $25+9=34$ words of six bits each: |
| − | :$$N_{\rm | + | :$$N_{\rm bits} = 34 \cdot 6 \hspace{0.15cm}\underline{= 204} \hspace{0.05cm},$$ |
i.e. a worse result than with seven bits according to subtask '''(5)'''. | i.e. a worse result than with seven bits according to subtask '''(5)'''. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Revision as of 17:40, 12 August 2021
We consider a binary source with the symbol set $\rm A$ and $\rm B$, where $\rm B$ however, occurs only very rarely.
- Without source coding, exactly one bit would be needed per source symbol, and accordingly, for a source symbol sequence of length $N$ would also apply to the coder symbol sequence $N_\text{bits} = N$.
- Entropy coding makes little sense here without further measures (example: combining several symbols into a tuple) because of the unfavourable symbol probabilities.
- The remedy is Run-Length Coding $(\rm RLC)$, which is described in the theory section under the link mentioned. For example, for the symbol sequence $\rm ABAABAAAABBAAB\text{...}$ the corresponding output of "Run–Length Coding": $ 2; \ 3; \ 5; \ 1; \ 3; \text{...}$
- Of course, the lengths $L_1 = 2$, $L_2 = 3$, ... of the individual substrings, each separated by $\rm B$ , must be represented in binary before transmission. If one uses $D = 3$ (bit) for all $L_i$ one obtains the RLC binary symbol sequence
- $$010\hspace{0.05cm}\text{'}\hspace{0.05cm}011\hspace{0.05cm}\text{'}\hspace{0.05cm}101\hspace{0.05cm}\text{'}\hspace{0.05cm}001\hspace{0.05cm}\text{'}\hspace{0.05cm}011\hspace{0.05cm}\text{'}\hspace{0.05cm}\text{...}$$
The graph shows the RLC result to be analysed. Columns 2 and 3 show the substring lengths $L_i$ in binary and decimal, respectively, and column 4 shows them in cumulative form (values from column 3 added up).
- One problem of "Run-Length Coding" $\rm (RLC)$ is the unlimited range of values of the quantities $L_i$. With $D = 3$, no value $L_i > 7$ can be represented and with $D = 2$, the restriction is $1 \le L_i \le 3$.
- The problem is circumvented with "Run–Length Limited Coding" $\rm (RLLC)$. If a value is $L_i \ge 2^D$, one replaces $L_i$ with a special character S and the difference $L_i - 2^D +1$. With the RLLC decoder, this special character S is expanded again.
Hints:
- This exercise belongs to the chapter Further source coding methods.
- In particular, reference is made to the page Run-Length Coding.
$\text{RLLC Example}$: We again assume the above sequence and the parameter $D = 2$ :
- Source symbol sequence: $\rm ABAABAAAABBAAB$...
- RLC decimal sequence: 2; 3; 5; 1; 3; ...
- RLLC decimal sequence: 2; 3; S; 2; 1; 3; ...
- RLLC binary sequence: 10′11′ 00′10′01′11′...
You can see:
- The special character S is binary-coded here as 00 . This is only an example – it does not have to be like this.
- Since with $D = 2$ for all real RLC values $1 \le L_i \le 3$ , the decoder recognizes the special character 00.
- It replaces this again with $2^D -1$ (three in the example) $\rm A$–symbols.
Questions
Solution
- This means that the same number of bits is needed without coding:
- $$N_\text{bits}\hspace{0.15cm}\underline{= 1250}.$$
(2) The entire symbol sequence of length $N = 1250$ contains $N_{\rm B} = 25$ symbols ${\rm B}$ and thus $N_{\rm A} = 1225$ symbols ${\rm A}$.
- The number $N_{\rm B}$ of symbols ${\rm B}$ is equal to the number of rows in the table given at the front.
- Thus the following applies to the relative frequency of symbol ${\rm B}$:
- $$h_{\rm B} = \frac{N_{\rm B}}{N} = \frac{25}{1250} \hspace{0.15cm}\underline{= 0.02} = 2\%\hspace{0.05cm}. $$
(3) We now consider "Run–Length Coding" $\rm (RLC)$, where each distance between two ${\rm B}$–symbols is represented by eight bits $(D = 8)$.
- Thus, with $N_{\rm B} = 25$, we get:
- $$N_{\rm bits} = N_{\rm B} \cdot 8 \hspace{0.15cm}\underline{= 200} \hspace{0.05cm}.$$
(4) $\rm RLC$ with $D = 7$ only allows values between $1$ und $2^7-1 =127$ for $L_i$.
- However, the entry "226" in line 19 is greater ⇒ NO.
(5) Even with Run–Length Limited Coding $\rm (RLLC)$, only values up to $127$ are permitted for the "real" distances $L_i$ with $D = 7$.
- The entry "226" in line 19 is replaced by the following for $\rm RLLC$:
- Line 19a: S = 0000000 ⇒ special character, stands for "+127",
- Line 19b: 1100011 ⇒ decimal 99.
- This gives a total of $26$ words of seven bits each:
- $$N_{\rm bits} = 26 \cdot 7 \hspace{0.15cm}\underline{= 182} \hspace{0.05cm}.$$
(6) With $D = 6$ the following changes have to be made in $\rm RLLC$ compared to $\rm RLC$ (see table):
- Line 1: $122 = 1 · 63 + 59$ (one word more),
- Line 6: $70 = 1 · 63 + 7$ (one word more),
- Line 7: $80 = 1 · 63 + 17$ (one word more),
- Line 12: $79 = 1 · 63 + 16$ (one word more),
- Line 13: $93 = 1 · 63 + 30$ (one word more),
- Line 19: $226 = 3 · 63 + 37$ (one word more),
- Line 25: $97 = 1 · 63 + 34$ (one word more).
This gives a total of $25+9=34$ words of six bits each:
- $$N_{\rm bits} = 34 \cdot 6 \hspace{0.15cm}\underline{= 204} \hspace{0.05cm},$$
i.e. a worse result than with seven bits according to subtask (5).