Aufgaben:Exercise 2.5: Distortion and Equalization

• Return to book

Trapezoidal spectrum (top) and
associated impulse response (bottom)

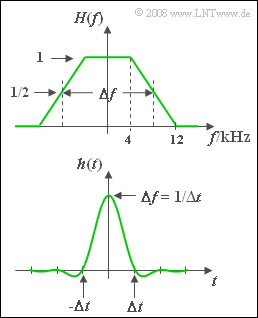
A communication system with input  $x(t)$  and output  $y(t)$, which is fully described by the trapezoidal frequency response  $H(f)$  according to the top graph, is considered. Using the roll-off factor  $r = 0.5$  and the equivalent bandwidth  $\Delta f = 16 \ \rm kHz$  the corresponding impulse response, which is computable by applying the inverse Fourier transform, is:

$$h(t) = \Delta f \cdot {\rm si}(\pi \cdot \Delta f \cdot t )\cdot {\rm si}(\pi \cdot r \cdot \Delta f \cdot t ) .$$

The available input signals are:

• The sum of two harmonic oscillations:

$$x_1(t) = {1\, \rm V} \cdot \cos(\omega_1 \cdot t) + {1\, \rm V} \cdot \sin(\omega_2 \cdot t).$$

Here, the following holds:  $\omega_1 = 2\pi \cdot 2000 \ {\rm 1/s}$  and  $\omega_2 \gt \omega_1$.

• A periodic triangular signal:

$$x_2(t) = \frac{8\, \rm V}{\pi^2} \cdot \big[\cos(\omega_0 t) + {1}/{9} \cdot \cos(3\omega_0 t) + {1}/{25} \cdot \cos(5\omega_0 t) + \hspace{0.05cm}\text{...}\big].$$

It should be noted that the fundamental frequency is  $f_0 = 2 \ \rm kHz$  or  $3\ \rm kHz$  beträgt. At time  $t = 0$  the signal value in both cases is  $1 \ \rm V$.

• A rectangular pulse  $x_3(t)$  with amplitude  $A = 1 \ \rm V$  and duration  $T = 1 \ \rm ms$. Since its spectrum  $X_3(f)$  extends to infinity,   $H(f)$  always results in linear distortions here.

From subtask  (6)  onwards it shall be attempted to eliminate the distortions possibly generated by  $H(f)$  by means of a downstream equaliser with

• frequency response  $H_{\rm E}(f)$,
• input signal  $y(t)$,  and
• output signal  $z(t)$.

Please note:

• The task belongs to the chapter  Linear Distortions.
• In particular, reference is made to the page  Entzerrungsverfahren.
• Der im Fragenkatalog verwendete Begriff "Gesamtverzerrung" bezieht sich auf das Eingangssignal  $x(t)$  und das Ausgangssignal  $z(t)$.

Questions

1

Welche Verzerrungsarten können bei diesem System ausgeschlossen werden?

	Nichtlineare Verzerrungen.
	Dämpfungsverzerrungen.
	Phasenverzerrungen.

2

Welche Eigenschaften zeigt das System beim Testsignal  $x_1(t)$  mit  $\underline{f_2 = 4 \ \rm kHz}$?

	Es wirkt wie ein ideales System.
	Es wirkt wie ein verzerrungsfreies System.
	Man erkennt, dass ein verzerrendes System vorliegt.

3

Welche Eigenschaften zeigt das System beim Testsignal  $x_1(t)$  mit  $\underline{f_2 = 10 \ \rm kHz}$?

	Es wirkt wie ein ideales System.
	Es wirkt wie ein verzerrungsfreies System.
	Man erkennt, dass ein verzerrendes System vorliegt.

4

Wie groß ist beim Testsignal  $x_2(t)$  mit  $\underline{f_0 = 3 \ \rm kHz}$  die Maximalabweichung  $\varepsilon_{\rm max} = |y_2(t_0) - x_2(t_0)|$.
An welcher Stelle  $t_0$  tritt  $\varepsilon_{\rm max}$  zum ersten Mal auf?

$\varepsilon_\text{max} \ = \ $ $\ \rm V$

$t_0 \ = \ $ $\ \rm ms$

5

Wie groß ist die maximale Abweichung  $\varepsilon_{\rm max}$  mit  $\underline{f_0 = 2 \ \rm kHz}$?

$\varepsilon_\text{max} \ = \ $ $\ \rm V$

6

Welchen Verlauf sollte der Entzerrer  $H_{\rm E}(f)$  besitzen, um alle Verzerrungen von  $H(f)$  bestmöglich zu kompensieren.
Welcher Betragswert ergibt sich bei  $\underline{f = 10 \ \rm kHz}$?

$|H_E(f = 10 \ \rm kHz)| \ = \ $

7

Bei welchen der aufgeführten Signale ist eine vollständige Entzerrung möglich?
Unter "vollständiger Entzerrung" soll dabei  $z(t) = x(t)$  verstanden werden.

	Beim Signal  $x_1(t)$  mit  $f_2 = 10 \ \rm kHz$,
	beim Signal  $x_2(t)$,
	beim Signal  $x_3(t)$.

Solution

Solution

(1)  Richtig sind die Lösungsvorschläge 1 und 3:

• Durch die Angabe eines Frequenzgangs wird bereits implizit ein lineares System vorausgesetzt, so dass nichtlineare Verzerrungen nicht auftreten können.
• Da  $H(f)$  rein reell ist, können Phasenverzerrungen ebenfalls ausgeschlossen werden.

(2)  Richtig sind die Lösungsvorschläge 1 und 2:

• Das Ausgangssignal ist  $y_1(t) = x_1(t)$.
• Somit ist das System nicht nur verzerrungsfrei, sondern kann für diese Anwendung auch als ideal bezeichnet werden.

(3)  Richtig ist der Lösungsvorschlag 3:

• In diesem Fall erhält man für das Ausgangssignal:

$$y_1(t)= 1\,{\rm V}\cdot \cos(2 \pi \cdot f_1 \cdot t) + {1}/{4}\cdot 1\,{\rm V}\cdot \sin(2 \pi \cdot f_2 \cdot t).$$

• Während der Anteil bei  $f_1$  unverändert übertragen wird, ist der Sinusanteil mit  $f_2$  auf ein Viertel gedämpft.
• Also liegen Dämpfungsverzerrungen vor.

(4)  Das Ausgangssignal  $y_2(t)$  hat die folgende Form, wenn man die Grundfrequenz  $f_0 = 3 \ \rm kHz$  berücksichtigt:

$$y_2(t)= \frac{8\,{\rm V}}{\pi^2} \left( \cos(\omega_0 t) + \frac{3}{8}\cdot \frac{1}{9} \cdot \cos(3\omega_0 t)\right) .$$

• Der Faktor  $3/8$  beschreibt  $H(f = 9 \ \rm kHz)$. Alle weiteren Spektralanteile bei  $15 \ \rm kHz$,  $21 \ \rm kHz$,  usw. werden vom System unterdrückt.

• Die stärksten Abweichungen zwischen  $x_2(t)$  und  $y_2(t)$  wird es bei den Dreieckspitzen geben, da sich hier die fehlenden hohen Frequenzen am stärksten auswirken. Zum Beispiel erhält man für den Zeitpunkt  $\underline{t= 0}$:

$$y_2(t=0)= \frac{8\,{\rm V}}{\pi^2} \left( 1 + {3}/{72}\right)= 0.844\,{\rm V} \hspace{0.3cm}\Rightarrow\hspace{0.3cm} \varepsilon_{\rm max} = |y_2(t=0)- x_2(t=0)| \hspace{0.15cm}\underline{= 0.156\,{\rm V}}.$$

(5)  Mit der Grundfrequenz  $f_0 = 2 \ \rm kHz$  sowie den Übertragungswerten  $H(3f_0) = 0.75$,  $H(5f_0) = 0.25$,  $H(7f_0) = 0$  ergibt sich:

$$y_2(t=0)= \frac{8\,{\rm V}}{\pi^2} \left( 1 + \frac{3}{4}\cdot \frac{1}{9} + \frac{1}{4} \cdot\frac{1}{25}\right)= 0.886\,{\rm V}\hspace{0.5cm} \Rightarrow \hspace{0.5cm}\varepsilon_{\rm max} \hspace{0.15cm}\underline{= 0.114\,{\rm V}}.$$

(6)  Im Bereich bis  $4 \ \rm kHz$  ist  $H_{\rm E}(f) = H(f) = 1$  zu setzen. Dagegen gilt im Bereich von  $4 \ \rm kHz$  bis  $12 \ \rm kHz$:

$$H_{\rm E}(f)= \frac{1}{H(f)} = \frac{1}{1.5 \cdot \big[1 - f/(12\,{\rm kHz})\big]} \hspace{0.5cm} \Rightarrow \hspace{0.5cm} H_{\rm E}(f = 10\,{\rm kHz})\hspace{0.15cm}\underline{= 4} .$$

Der Nennerausdruck beschreibt hierbei die Geradengleichung des Flankenabfalls.

(7)  Richtig ist der Lösungsvorschlag 1:

• Sowohl  $x_2(t)$  als auch  $x_3(t)$  beinhalten auch Spektralanteile bei Frequenzen größer als  $12 \ \rm kHz$.
• Wurden diese von  $H(f)$  abgeschnitten   ⇒   Bandbegrenzung, so können sie durch den Entzerrer nicht mehr rekonstruiert werden.
• Das heißt, dass nur das Signal  $x_1(t)$  durch  $H_{\rm E}(f)$  wieder hergestellt werden kann, allerdings nur dann, wenn  $f_2 < 12 \ \rm kHz$ gilt:

$$z_1(t)= \underline{1} \cdot 1\,{\rm V}\cdot \cos(2 \pi \cdot f_1 \cdot t) + \underline{4} \cdot \frac{1}{4}\cdot 1\,{\rm V}\cdot \sin(2 \pi \cdot f_2 \cdot t).$$

• Die jeweils ersten (unterstrichenen) Faktoren geben jeweils die Verstärkungswerte von  $H_{\rm E}(f)$  an.