Aufgaben:Exercise 2.5Z: Nyquist Equalization

• Return to book

Block diagram for the considered Nyquist system

A digital baseband transmission system is modelled by the depicted block diagram.

• The "transmitter", "channel" and "receiver" components are described in the frequency domain by  $H_{\rm S}(f)$,  $H_{\rm K}(f)$  and  $H_{\rm E}(f)$ .

• The overall frequency response  $H(f) = H_{\rm S}(f) \cdot H_{\rm K}(f) \cdot H_{\rm E}(f)$  has a  $\cos^2$–shaped curve:

$$H(f) = \left\{ \begin{array}{c} \cos^2\left({\pi}/{2} \cdot f \cdot T \right) \\ 0 \\ \end{array} \right.\quad \quad \begin{array}{*{10}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.005cm} f\hspace{0.05cm} \right| < 1/T,} \\ {\left|\hspace{0.005cm} f \hspace{0.05cm} \right| \ge 1/T.} \\ \end{array}$$

• The signal  $y(t)$  before the decision circuit thus exhibits equidistant zero crossings at intervals of  $T$ .
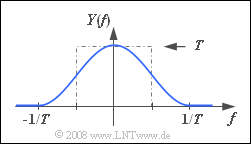
• It is assumed here that the source emits a  Dirac-delta  $x(t)$  with weight  $T$  (see graph).

It is pointed out that this is a so-called "Nyquist system".

Wie im Buch  Digital Signal Transmission  noch ausführlich diskutiert werden wird, stellen diese Nyquistsysteme eine wichtige Klasse digitaler Übertragungssysteme dar, da sich bei ihnen die sequenziell übertragenen Symbole nicht gegenseitig beeinflussen.

Für die Lösung dieser Aufgabe werden diese weiterreichenden Aspekte jedoch nicht benötigt.

Es wird hier lediglich vorausgesetzt, dass

• der Sendeimpuls  $s(t)$  rechteckförmig sei mit Impulsdauer  $T$:

$$H_{\rm S}(f) = {\rm si}(\pi f T),$$

• der Kanal bis einschließlich Teilaufgabe  (2)  als ideal vorausgesetzt wird, während für die letzte Teilaufgabe  (3)  gelten soll:

$$H_{\rm K}(f) = H_{\rm G}(f) = {\rm e}^{-\pi(f \cdot T)^2} .$$

Gesucht ist für beide Kanäle der Empfänger– und gleichzeitig Entzerrerfrequenzgang  $H_{\rm E}(f)$, damit der Gesamtfrequenzgang die gewünschte Nyquistform aufweist.

Please note:

• The task belongs to the chapter  Linear Distortions.

• Als bekannt vorausgesetzt wird die folgende trigonometrische Beziehung:

$$\frac{\cos^2(\alpha /2)}{\sin(\alpha )} = {1}/{2} \cdot {\rm cot}(\alpha /2) .$$

Questions

1

Berechnen Sie den Ausgangssignalwert zum Zeitpunkt  $t = 0$.

$y(t = 0) \ = \ $

2

Zunächst sei  $H_{\rm K}(f) = 1$   ⇒   idealer Kanal. Berechnen Sie für diesen Fall den Frequenzgang  $H_{\rm E}(f)$.
Welche Werte ergeben sich bei den nachfolgend genannten Frequenzen?

$|H_{\rm E}(f \cdot T = 0)| \ = \ $

$|H_{\rm E}(f \cdot T = 0.25)|\ = \ $

$|H_{\rm E}(f \cdot T = 0.50)|\ = \ $

$|H_{\rm E}(f \cdot T = 0.75)|\ = \ $

$|H_{\rm E}(f \cdot T = 1.00)|\ = \ $

3

Berechnen Sie  $H_{\rm E}(f)$  für den gaußförmigen Kanal  $H_{\rm K}(f) = H_{\rm G}(f)$  entsprechend der Angabe.

$|H_{\rm E}(f \cdot T = 0)|\ = \ $

$|H_{\rm E}(f \cdot T = 0.25)| \ = \ $

$|H_{\rm E}(f \cdot T = 0.50)|\ = \ $

$|H_{\rm E}(f \cdot T = 0.75)|\ = \ $

$|H_{\rm E}(f \cdot T = 1.00)|\ = \ $

Solution

Solution

Cosinus–Quadrat–Spektrum

(1)  Mit dem konstanten Spektrum  $X(f) = T$  erhält man für die Spektralfunktion des Empfängerausgangssignals  $y(t)$:

$$Y(f)= T \cdot {H(f)}.$$

• Der Signalwert bei  $t = 0$  ist gleich der Fläche unter $Y(f)$.
• Wie aus der nebenstehenden Skizze hervorgeht, ist diese gleich  $1$. Daraus folgt:

$$y(t = 0)\; \underline{= 1}.$$

Frequenzgang des Nyquistentzerrers

(2)  Aus der Bedingung  $H_{\rm S}(f) \cdot H_{\rm E}(f) = H(f)$  folgt im betrachteten Bereich:

$$H_{\rm E}(f)= \frac{H(f)}{H_{\rm S}(f)} = \frac{\cos^2(\pi f T/2)}{\sin(\pi f T)/(\pi f T)}.$$

• Wegen  $\cos(0) = 1$  und  ${\rm si}(0) = 1$  gilt auch  $H_{\rm E}(f = 0)\;\underline{=1}$.

• Mit der gegebenen trigonometrischen Umformung gilt weiter:

$$H_{\rm E}(f) = {\pi f T}/{2} \cdot {\rm cot}\left( {\pi f T}/{2}\right),$$

$$H_{\rm E}(f \cdot T = 0.25) = {\pi }/{8} \cdot {\rm cot}\left( 22.5^{\circ}\right) = {\pi }/{8} \cdot 2.414 = \hspace{0.15cm}\underline{0.948},$$

$$H_{\rm E}(f \cdot T = 0.50) = {\pi }/{4} \cdot {\rm cot}\left( 45^{\circ}\right) = {\pi }/{4} \cdot 1 \hspace{0.15cm}\underline{= 0.785},$$

$$ H_{\rm E}(f \cdot T = 0.75) = {3 \pi }/{8} \cdot {\rm cot}\left( 67.5^{\circ}\right) = {3 \pi }/{8} \cdot 0.414 \hspace{0.15cm}\underline{= 0.488},$$

$$ H_{\rm E}(f \cdot T = 1.00)= { \pi }/{2} \cdot {\rm cot}\left( 90^{\circ}\right) ={ \pi }/{2} \cdot 0 \hspace{0.15cm}\underline{ = 0}.$$

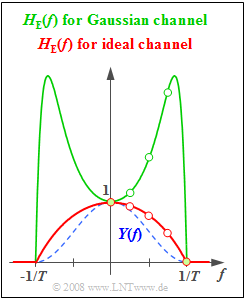
(3)  Unter Berücksichtigung des Gaußkanals gilt: $$H_{\rm E}(f)= \frac{H(f)}{H_{\rm S}(f) \cdot H_{\rm K}(f)} = H_{\rm E}^{(2)}(f)\cdot {\rm e}^{\pi (f\hspace{0.05cm}\cdot \hspace{0.05cm} T)^2}.$$

Hierbei bezeichnet  $H_{\rm E}^{(2)}(f)$  den bei der Teilaufgabe  (2)  berechneten Entzerrerfrequenzgang unter der Voraussetzung eines idealen Kanals. Man erhält folgende numerische Ergebnisse:

$$H_{\rm E}(f\cdot T = 0) = 1 \cdot {\rm e}^{0} \hspace{0.15cm}\underline{= 1},$$

$$H_{\rm E}(f \cdot T = 0.25) = 0.948 \cdot 1.217 \hspace{0.15cm}\underline{= 1.154},$$

$$H_{\rm E}(f \cdot T = 0.50) = 0.785 \cdot 2.193 \hspace{0.15cm}\underline{= 1.722},$$

$$H_{\rm E}(f \cdot T = 0.75) = 0.488 \cdot 5.854 \hspace{0.15cm}\underline{= 2.857},$$

$$H_{\rm E}(f \cdot T = 1.00) = 0 \cdot 23.141 \hspace{0.15cm}\underline{= 0}.$$

Die grüne Kurve in obiger Grafik fasst die Ergebnisse dieser Teilaufgabe zusammen.