Difference between revisions of "Aufgaben:Exercise 4.5: Coaxial Cable - Impulse Response"
| Line 3: | Line 3: | ||
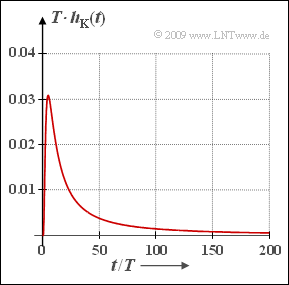
[[File:P_ID1814__LZI_A_4_5.png|right|frame|Impulse response of a coaxial cable]] | [[File:P_ID1814__LZI_A_4_5.png|right|frame|Impulse response of a coaxial cable]] | ||
| − | The frequency response of a coaxial cable of length $l$ can be represented by the following formula: | + | The frequency response of a coaxial cable (German: "Koaxialkabel" ⇒ subscipt "K") of length $l$ can be represented by the following formula: |
:$$H_{\rm K}(f) = {\rm e}^{- \alpha_0 \hspace{0.05cm} \cdot \hspace{0.05cm} l} | :$$H_{\rm K}(f) = {\rm e}^{- \alpha_0 \hspace{0.05cm} \cdot \hspace{0.05cm} l} | ||
\cdot | \cdot | ||
| Line 9: | Line 9: | ||
{\rm e}^{- (\alpha_2 + {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} \beta_2) \hspace{0.05cm}\cdot \sqrt{f} \hspace{0.05cm}\cdot \hspace{0.05cm}l} | {\rm e}^{- (\alpha_2 + {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} \beta_2) \hspace{0.05cm}\cdot \sqrt{f} \hspace{0.05cm}\cdot \hspace{0.05cm}l} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | The first term of this equation is due to the ohmic losses, the second term to the transverse losses. Dominant, however, is the skin effect, which is expressed by the third term. | + | The first term of this equation is due to the ohmic losses, the second term to the transverse losses. Dominant, however, is the skin effect, which is expressed by the third term. |
| − | With the coefficients valid for | + | With the coefficients valid for the "standard coaxial cable" $\text{(2.6 mm}$ core diameter, $\text{9.5 mm}$ outer diameter$)$ |
:$$\alpha_2 = 0.2722 \hspace{0.15cm}\frac {\rm Np}{\rm km \cdot \sqrt{\rm MHz}} | :$$\alpha_2 = 0.2722 \hspace{0.15cm}\frac {\rm Np}{\rm km \cdot \sqrt{\rm MHz}} | ||
\hspace{0.05cm}, | \hspace{0.05cm}, | ||
| Line 22: | Line 22: | ||
\hspace{0.05cm}\cdot \sqrt{f/{\rm MHz}}} | \hspace{0.05cm}\cdot \sqrt{f/{\rm MHz}}} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | That means: | |
| + | |||
| + | Attenuation curve ${a}_{\rm K}(f)$ and phase curve $b_{\rm K}(f)$ are identical except for the pseudo units "Np" and "rad", respectively. | ||
| Line 28: | Line 30: | ||
:$${a}_{\rm \star} = {a}_{\rm K}(f ={R}/{2}) | :$${a}_{\rm \star} = {a}_{\rm K}(f ={R}/{2}) | ||
\hspace{0.3cm}\Rightarrow \hspace{0.3cm}H_{\rm K}(f) = {\rm e}^{- | \hspace{0.3cm}\Rightarrow \hspace{0.3cm}H_{\rm K}(f) = {\rm e}^{- | ||
| − | {a}_{\rm \star} \cdot \sqrt{2f/R}}\cdot {\rm e}^{- {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} {a}_{\star} \cdot \sqrt{2f/R}}\hspace{0.4cm}{\rm | + | {a}_{\rm \star} \cdot \sqrt{2f/R}}\cdot {\rm e}^{- {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} {a}_{\star} \cdot \sqrt{2f/R}}\hspace{0.4cm}{\rm with}\hspace{0.2cm}{a}_{\star}\hspace{0.2cm}{\rm in}\hspace{0.2cm}{\rm Np} |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | *The corresponding $\rm dB$& | + | *The corresponding $\rm dB$ value is greater by a factor of $8.686$. |
| − | *For a binary system, $R = 1/T$ holds, so that the characteristic cable attenuation refers to the frequency $f = 1/(2T)$ | + | *For a binary system, $R = 1/T$ holds, so that the characteristic cable attenuation refers to the frequency $f = 1/(2T)$. |
| − | The [[Signal_Representation/Fourier_Transform_and_Its_Inverse#Fouriertransformation|Fourier transform]] of $H_{\rm K}(f)$ yields the impulse response $h_{\rm K}(t)$, which can be specified in closed-analytic form for a coaxial cable using the approximations described here. For a binary system holds: | + | The [[Signal_Representation/Fourier_Transform_and_Its_Inverse#Fouriertransformation|Fourier transform]] of $H_{\rm K}(f)$ yields the impulse response $h_{\rm K}(t)$, which can be specified in closed-analytic form for a coaxial cable using the approximations described here. For a binary system holds: |
:$$h_{\rm K}(t) = \frac{ {a}_{\rm \star}/T}{ \sqrt{2 \pi^2 \cdot (t/T)^3}}\hspace{0.1cm} \cdot | :$$h_{\rm K}(t) = \frac{ {a}_{\rm \star}/T}{ \sqrt{2 \pi^2 \cdot (t/T)^3}}\hspace{0.1cm} \cdot | ||
{\rm e}^{ - {{a}_{\rm \star}^2}/(2 \hspace{0.05cm} \pi \cdot \hspace{0.05cm} t/T)} | {\rm e}^{ - {{a}_{\rm \star}^2}/(2 \hspace{0.05cm} \pi \cdot \hspace{0.05cm} t/T)} | ||
\hspace{0.4cm}{\rm with}\hspace{0.2cm}{a}_{\rm \star}\hspace{0.2cm}{\rm in}\hspace{0.2cm}{\rm Np} | \hspace{0.4cm}{\rm with}\hspace{0.2cm}{a}_{\rm \star}\hspace{0.2cm}{\rm in}\hspace{0.2cm}{\rm Np} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | Subtask '''(5)''' refers to the basic | + | Subtask '''(5)''' refers to the basic reception pulse $g_r(t) = g_s(t) \star h_{\rm K}(t)$, where the basic transmission pulse $g_s(t)$ is assumed to be a rectangle $($height $s_0$, duration $T)$. |
| − | |||
| − | |||
| − | |||
| − | + | Notes: | |
*The exercise belongs to the chapter [[Linear_and_Time_Invariant_Systems/Eigenschaften_von_Koaxialkabeln|Properties of Coaxial Cables]]. | *The exercise belongs to the chapter [[Linear_and_Time_Invariant_Systems/Eigenschaften_von_Koaxialkabeln|Properties of Coaxial Cables]]. | ||
| − | *You can use the interactive applet [[Applets:Zeitverhalten_von_Kupferkabeln|Zeitverhalten von Kupferkabeln]] to check your results. | + | *You can use the (German language) interactive SWF applet [[Applets:Zeitverhalten_von_Kupferkabeln|"Zeitverhalten von Kupferkabeln"]] ⇒ "Time behavior of copper cables" to check your results. |
Revision as of 18:27, 12 November 2021
The frequency response of a coaxial cable (German: "Koaxialkabel" ⇒ subscipt "K") of length $l$ can be represented by the following formula:
- $$H_{\rm K}(f) = {\rm e}^{- \alpha_0 \hspace{0.05cm} \cdot \hspace{0.05cm} l} \cdot {\rm e}^{- (\alpha_1 + {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} \beta_1) \hspace{0.05cm}\cdot f \hspace{0.05cm}\cdot \hspace{0.05cm}l} \cdot {\rm e}^{- (\alpha_2 + {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} \beta_2) \hspace{0.05cm}\cdot \sqrt{f} \hspace{0.05cm}\cdot \hspace{0.05cm}l} \hspace{0.05cm}.$$
The first term of this equation is due to the ohmic losses, the second term to the transverse losses. Dominant, however, is the skin effect, which is expressed by the third term.
With the coefficients valid for the "standard coaxial cable" $\text{(2.6 mm}$ core diameter, $\text{9.5 mm}$ outer diameter$)$
- $$\alpha_2 = 0.2722 \hspace{0.15cm}\frac {\rm Np}{\rm km \cdot \sqrt{\rm MHz}} \hspace{0.05cm}, \hspace{0.2cm} \beta_2 = 0.2722 \hspace{0.15cm}\frac {\rm rad}{\rm km \cdot \sqrt{\rm MHz}}\hspace{0.05cm}$$
this frequency response can also be represented as follows:
- $$H_{\rm K}(f) \approx {\rm e}^{- 0.2722 \hspace{0.05cm}\cdot \hspace{0.05cm}l/{\rm km} \hspace{0.05cm}\cdot \sqrt{f/{\rm MHz}} } \cdot {\rm e}^{- {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} 0.2722 \hspace{0.05cm}\cdot \hspace{0.05cm}l/{\rm km} \hspace{0.05cm}\cdot \sqrt{f/{\rm MHz}}} \hspace{0.05cm}.$$
That means:
Attenuation curve ${a}_{\rm K}(f)$ and phase curve $b_{\rm K}(f)$ are identical except for the pseudo units "Np" and "rad", respectively.
If one defines the characteristic cable attenuation ${a}_{\rm *}$ at half the bit rate $($i.e., at $R/2)$ and normalizes the frequency to $R$, one can treat digital systems of different bit rate and length uniformly:
- $${a}_{\rm \star} = {a}_{\rm K}(f ={R}/{2}) \hspace{0.3cm}\Rightarrow \hspace{0.3cm}H_{\rm K}(f) = {\rm e}^{- {a}_{\rm \star} \cdot \sqrt{2f/R}}\cdot {\rm e}^{- {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} {a}_{\star} \cdot \sqrt{2f/R}}\hspace{0.4cm}{\rm with}\hspace{0.2cm}{a}_{\star}\hspace{0.2cm}{\rm in}\hspace{0.2cm}{\rm Np} \hspace{0.05cm}.$$
- The corresponding $\rm dB$ value is greater by a factor of $8.686$.
- For a binary system, $R = 1/T$ holds, so that the characteristic cable attenuation refers to the frequency $f = 1/(2T)$.
The Fourier transform of $H_{\rm K}(f)$ yields the impulse response $h_{\rm K}(t)$, which can be specified in closed-analytic form for a coaxial cable using the approximations described here. For a binary system holds:
- $$h_{\rm K}(t) = \frac{ {a}_{\rm \star}/T}{ \sqrt{2 \pi^2 \cdot (t/T)^3}}\hspace{0.1cm} \cdot {\rm e}^{ - {{a}_{\rm \star}^2}/(2 \hspace{0.05cm} \pi \cdot \hspace{0.05cm} t/T)} \hspace{0.4cm}{\rm with}\hspace{0.2cm}{a}_{\rm \star}\hspace{0.2cm}{\rm in}\hspace{0.2cm}{\rm Np} \hspace{0.05cm}.$$
Subtask (5) refers to the basic reception pulse $g_r(t) = g_s(t) \star h_{\rm K}(t)$, where the basic transmission pulse $g_s(t)$ is assumed to be a rectangle $($height $s_0$, duration $T)$.
Notes:
- The exercise belongs to the chapter Properties of Coaxial Cables.
- You can use the (German language) interactive SWF applet "Zeitverhalten von Kupferkabeln" ⇒ "Time behavior of copper cables" to check your results.
Questions
Solution
- $$\alpha_2 \cdot l \cdot {R}/{2} = 6.9\,\,{\rm Np} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} l = \frac{6.9\,\,{\rm Np}}{0.2722 \,\, {\rm Np}/({\rm km \cdot \sqrt{\rm MHz}}) \cdot \sqrt{70\,\,{\rm MHz}}}\hspace{0.15cm}\underline{ \approx 3\,\,{\rm km}} \hspace{0.05cm}.$$
(2) Mit den Substitutionen
- $$x = \frac{ t}{ T}, \hspace{0.2cm} K_1 = \frac{ {a}_{\rm \star}/T}{\sqrt{2 \pi^2 }}, \hspace{0.2cm} K_2 = \frac{ {a}_{\rm \star}^2}{2 \pi}$$
kann die Impulsantwort wie folgt beschrieben werden:
- $$h_{\rm K}(x) = K_1 \cdot x^{-3/2}\cdot {\rm e}^{-K_2/x} \hspace{0.05cm}.$$
- Durch Nullsetzen der Ableitung folgt daraus:
- $$- {3}/{2} \cdot K_1 \cdot x^{-5/2}\cdot {\rm e}^{-K_2/x}+ K_1 \cdot x^{-3/2}\cdot {\rm e}^{-K_2/x}\cdot (-K_2) \cdot (-x^{-2})= 0 \hspace{0.05cm}.$$
- $$\Rightarrow \hspace{0.3cm} {3}/{2} \cdot x^{-5/2} = K_2 \cdot x^{-7/2} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} x_{\rm max} = {2}/{3} \cdot K_2 = \frac{{a}_{\rm \star}^2}{3 \pi} \hspace{0.05cm}.$$
- Daraus ergibt sich für $60 \ \rm dB$ Kabeldämpfung $({a}_{\rm \star} \approx 6.9 \ \rm Np)$:
- $$x_{\rm max} = { t_{\rm max}}/{ T}= { 6.9^2}/{(3\pi)}\hspace{0.15cm}\underline{ \approx 5 }\hspace{0.05cm}.$$
(3) Setzt man das Ergebnis in die vorgegebene Gleichung ein, so erhält man (zur Vereinfachung verwenden wir "${a}$"anstelle von "${a}_{\rm \star}$"):
- $$h_{\rm K}(t_{\rm max}) = \frac{1}{T} \cdot \frac{ {a}}{ \sqrt{2 \pi^2 \cdot {{a}^6}/{(3\pi)^3}}}\hspace{0.1cm} \cdot {\rm exp} \left[ - \frac{{a}^2}{2\pi} \cdot \frac{3\pi}{{\rm a}^2}\hspace{0.1cm}\right] = \frac{1}{T} \cdot \frac{1}{{a}^2}\cdot \sqrt{\frac{27 \pi }{2}} \cdot {\rm e}^{-3/2} \approx \frac{1}{T} \cdot \frac{1.453}{{a}^2} \hspace{0.05cm}.$$
- Mit $a = 6.9$ kommt man somit zum Endergebnis:
- $${\rm Max}\,[h_{\rm K}(t)] = \frac{1.453}{{6.9\,}^2} \cdot {1}/{T}\hspace{0.15cm}\underline{\approx 0.03 \cdot {1}/{T}} \hspace{0.05cm}.$$
(4) Mit dem Ergebnis aus (3) lautet die geeignete Bestimmungsgleichung:
- $$\frac{ {a}/T}{ \sqrt{2 \pi^2 \cdot (t_{5\%}/T)^3}}= 0.05 \cdot 0.03 {1}/{T} \hspace{0.15cm}{= 0.0015 \cdot {1}/{T}} \hspace{0.2cm} \Rightarrow \hspace{0.2cm} (t_{5\%}/T)^{3/2} = \frac{a}{\sqrt{2} \cdot \pi \cdot 0.0015}\approx 1036 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \hspace{0.15cm}\underline{t_{5\%}/T \approx 103.5} \hspace{0.05cm}.$$
- Dieser Wert ist etwas zu groß, da der zweite Term ${\rm e}^{-0.05}\approx 0.95$ vernachlässigt wurde.
- Die exakte Berechnung liefert $t_{\rm 5\%}/T \approx 97$.
(5) Richtig ist der zweite Lösungsvorschlag:
- Allgemein gilt:
- $$g_r(t) = g_s(t) \star h_{\rm K}(t) = s_0 \cdot \int_{t-T/2}^{t+T/2} h_{\rm K}(\tau) \,{\rm d} \tau .$$
- Da sich die Kanalimpulsantwort $h_{\rm K}(t)$ innerhalb einer Symboldauer nur unwesentlich ändert, kann auch geschrieben werden:
- $$g_r(t) = h_{\rm K}(t) \cdot s_0 \cdot T.$$