Aufgaben:Exercise 2.1Z: DSB-AM without/with Carrier

• Return to book

Die bei der AM beteiligten Signale

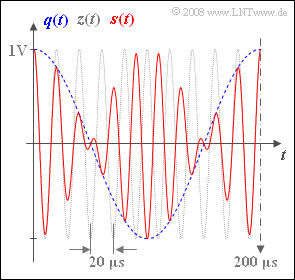
The red curve on the graph shows a section of the transmitted signal  $s(t) = q(t) · z(t)$  of a double-sideband amplitude modulation (abbreviated as DSB-AM) without carrier.   (abgekürzt mit ZSB-AM)  ohne Träger. The duration of the time interval is  $\rm 200 \ µ s$.

Additionally plotted in the graph are:

• the source signal (as a blue dashed curve):

$$q(t) = 1\,{\rm V} \cdot \cos(2 \pi f_{\rm N} t + \phi_{\rm N}),$$

• the carrier signal (gray-dotted trace):

$$z(t) = 1 \cdot \cos(2 \pi f_{\rm T} t + \phi_{\rm T})$$

From subtask (4) onwards, the "DSB-AM with carrier" is considered. In that case, with  $A_{\rm T} = 2\text{ V}$:

$$s(t) = \left(q(t) + A_{\rm T} \right) \cdot z(t) \hspace{0.05cm}.$$

Hints:

• This exercise belongs to the chapter  Double-Sideband Amplitude Modulation.
• Particlar reference is made to the pages  Description in the time domain  and  Double-Sideband Amplitude Modulation with carrier.

Fragebogen

1

From the graph, determine the phase values of the source and carrier signals.

$\phi_{\rm N} \ = \ $ $\ \text{degrees}$

$\phi_{\rm T} \ = \ $ $\ \text{degrees}$

2

What is the frequency $f_{\rm N}$  of the message signal  $q(t)$  and what is the frequency $f_{\rm T}$  of the carrier signal  $z(t)$?

$f_{\rm N} \ = \ $ $\ \text{kHz}$

$f_{\rm T} \ = \ $ $\ \text{kHz}$

3

Analyze the zero crossings of  $s(t)$. Which statements are true?

	All zero crossings of  $z(t)$  are preserved in  $s(t)$ .
	There are additional zero crossings caused by  $q(t)$.
	$s(t) = a(t) · \cos(ω_T · t)$  holds with  $a(t) = |q(t)|$.

4

Determine the spectral function  $S(f)$  by convolution.  Which (positive) frequencies $f_1$  and $f_2 > f_1$  are included in the signal??

$f_1 \ = \ $ $\ \text{kHz}$

$f_2\ = \ $ $\ \text{kHz}$

5

Let  $A_{\rm T} = 2\text{ V}$.  What is the modulation depth  $m$?

$m \ = \ $

6

WWhich of the statements are true for   „DSB–AM with carrier”  and  $A_{\rm T} = 2\text{ V}$ ?

	$S(f)$  now includes Dirac functions at  $±f_{\rm T}$.
	The weights of these Dirac lines are each  $2\text{ V}$.
	$q(t)$  can be seen in the envelope of  $s(t)$ .
	Due to the additional carrier component, the power remains unchanged..

Solution

Solution

(1)  Beide Signale sind cosinusförmig   ⇒   $ϕ_{\rm N} \hspace{0.15cm}\underline { = 0}$  und  $ϕ_{\rm T} \hspace{0.15cm}\underline { = 0}$.

(2)  Aus der Grafik können für  $q(t)$  und $z(t)$ die Periodendauern  $200$ μs  bzw.  $20$ μs  abgelesen werden.

• Daraus ergeben sich die Frequenzen zu  $f_{\rm N} \hspace{0.15cm}\underline { = 5}$  kHz und  $f_{\rm T} \hspace{0.15cm}\underline { = 50}$ kHz.

(3)  Richtig sind die Lösungsvorschläge 1 und 2:

• Die Nullstellen von  $z(t)$  bei  $±5$ μs,  $±15$ μs,  $±25$ μs, ... sind auch im Signal  $s(t)$  vorhanden   ⇒   Aussage 1 ist richtig.
• Weitere Nullstellen von  $s(t)$ – verursacht durch  $q(t)$  – liegen bei  $±50$ μs,  $±150$ μs,  $±250$ μs, ....   ⇒   Aussage 2 ist richtig.
• Die dritte Aussage trifft dagegen nicht zu, sondern es gilt:   $ s(t) = a(t) \cdot \cos[\omega_{\rm T} t + \phi (t)] \hspace{0.05cm}.$
• Für  $q(t) > 0$  ist die Phasenfunktion  $ϕ(t) = 0$  und  $s(t)$  ist gleichlaufend mit  $z(t)$.
• Dagegen gilt für  $q(t) < 0$:   $ϕ(t) = π = 180^\circ$.
• Bei den Nulldurchgängen von  $q(t)$  weist das modulierte Signal  $s(t)$  Phasensprünge auf.

ZSB–AM–Spektrum  $Z(f)$,  $Q(f)$  und  $S(f)$

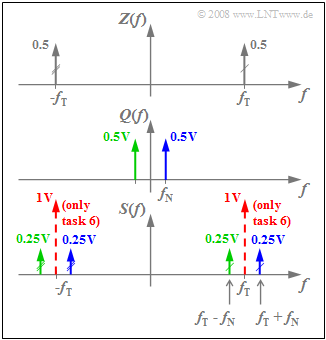
(4)  Das Spektrum  $S(f)$  ergibt sich aus der Faltung der Spektralfunktionen  $Z(f)$  und  $Q(f)$, die jeweils aus nur zwei Diracfunktionen bestehen.  Die Grafik zeigt das Ergebnis.

• Die rot eingezeichneten Diracfunktionen gelten nur für die  „ZSB–AM mit Träger”  und beziehen sich auf die Teilaufgabe  (6).
• Die Faltung der beiden  $Z(f)$–Diracfunktionen bei  $f_{\rm T} = 50\text{ kHz}$  mit  $Q(f)$  führt zu den Diraclinien bei  $f_{\rm T} - f_{\rm N}$  und  $f_{\rm T} + f_{\rm N}$, jeweils mit Gewicht  $0.5 · 0.5\text{ V}= 0.25\text{ V}$.
• Die gesuchten Werte sind somit  $f_1\hspace{0.15cm}\underline { = 45 \ \rm kHz}$  und  $f_1\hspace{0.15cm}\underline { = 55 \ \rm kHz}$.
• Die mit zwei Markierungsstrichen versehene Diracfunktion  $0.5 · δ(f + f_{\rm T})$  führt zu zwei weiteren Diraclinien bei  $-f_1$  und  $-f_2$.

(5)  Der Modulationsgrad berechnet sich zu:

$$ m = \frac{q_{\rm max}}{A_{\rm T}} = \frac{A_{\rm N}}{A_{\rm T}} \hspace{0.15cm}\underline {= 0.5} \hspace{0.05cm}.$$

(6)  Richtig sind die Lösungsvorschläge 1 und 3:

• Gemäß der Skizze ergeben sich Diraclinien bei  $±f_{\rm T}$, beide mit dem Impulsgewicht  $A_{\rm T}/2 = 1\text{ V}$.
• Bei  $m ≤ 1$  ist  $q(t)$  in der Hüllkurve erkennbar und Hüllkurvendemodulation anwendbar.
• Allerdings muss diese einfachere Empfängervariante durch eine sehr viel größere Sendeleistung erkauft werden. 
• In diesem Beispiel  $(m = 0.5)$  wird die Sendeleistung durch den Trägerzusatz verneunfacht.