Aufgaben:Exercise 1.3: Fictional University Somewhere

• Return to book

Fictional University Somewhere

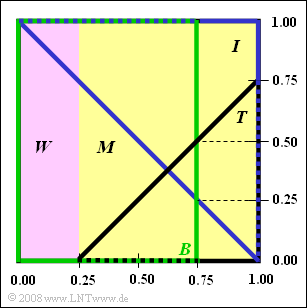
From the adjacent graph you can read some information about  $\rm FUS$  ("Fictional University Somewhere").  The whole square represents the universal set  $G$  of  $960$  students.  Of these

• $25\%$  female  (German:  "weiblich")   (set  $W$,  purple rectangle),
• $75\%$  male  (German:  "männlich")   (set  $M$,  yellow rectangle).

At the university there are the faculties of

• Theology  (set  $T$,nbsp; black triangle),
• Information Technology  (set  $I$,nbsp; blue triangle),
• Business Administration  (set  $B$,nbsp; green rectangle).

Each student must be assigned to at least one of these faculties,nbsp; but can belong to two or three faculties at the same time.

Hints:

• The exercise belongs to the chapter  Set Theory Basics.
• The topic of this chapter is illustrated with examples in the  (German language)  learning video

Mengentheoretische Begriffe und Gesetzmäßigkeiten   $\Rightarrow$   "Set Theoretical Concepts and Laws".

• The areas in the above diagram are to scale,&nbsp, so you can easily give the  (percentage)  occupancy figures using the numerical values given and simple geometric considerations.

Questions

1

Calculate the number of students enrolled in the faculties.  As a check,  enter the number of students in the Faculty of Theology  $(N_{\rm T})$.

$N_{\rm T} \ = \ $

2

Which of the following statements are true?

	$I$  is a subset of  $M$.
	$W$  is a subset of  $B$.
	$W$  and  $M$  together form a  "complete system".
	$B$,  $I$  and  $T$  together form a  "complete system".
	$W$  and  $T$  are disjoint sets.
	The union of  $B$,  $I$  and  $T$  gives the universal set  $G$.
	The intersection of  $B$,  $I$  and  $T$  gives the empty set  $\phi$.

3

What is the proportion of female IT students relative to all students?

$\text{Pr}\big[\text{female IT student}\big] \ = \ $ $\ \%$

4

What is the proportion of students with only one field of study?

$\text{Pr}\big[\text{one field of study}\big] \ = \ $ $\ \%$

5

What is the percentage of students with three fields of study?

$\text{Pr}\big[\text{three fields of study}\big] \ = \ $ $\ \%$

6

What is the percentage of students with two fields of study?

$\text{Pr}\big[\text{two fields of study}\big] \ = \ $ $\ \%$

Solution

Solution

(1)  From simple geometric considerations, we arrive at the results:

$${\rm Pr}(B) = 3/4 \cdot 1 = 3/4\hspace{0.3cm}(\text{absolute:}\ 720),$$

$${\rm Pr}(I) = {1}/{2}\cdot 1\cdot 1 = 1/2\hspace{0.3cm}(\text{absolute:} \ 480),$$

$${\rm Pr}(T) = {1}/{2} \cdot {3}/{4} \cdot {3}/{4} = {9}/{32} \hspace{0.3cm}(\text{absolute:}\ 270)\hspace{0.3cm}\Rightarrow \hspace{0.3cm}N_{\rm T} \;\underline{= 270}.$$

(2)  Proposed solutions 2, 3, 5 and 6 are correct   ⇒   proposed solutions 1, 4, 7 are consequently incorrect:

• There are also female IT students, although very few.
• The union of  $B$,  $I$  and  $T$  gives the universal set, but not a complete system (not all combinations of  $B$,  $I$  and  $T$  are disjoint).
• For the same reason, the intersection of  $B$,  $I$  and  $T$  does not yield the empty set.

Geometric solution of a probability problem

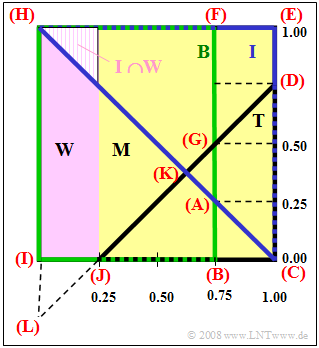
(3)  In set theory, an IT student is the intersection of  $I$  and  $W$ 
(shown as a shaded area in the upper left of the graph):

$$\text{Pr[female IT student] = Pr}(I \cap W) = {1}/{2}\cdot {1}/{4} \cdot {1}/{4} = {1}/{32} \hspace{0.15cm}\underline { \thickapprox 3.13 \%}.$$

In words, there are  $30$  female IT students among the  $960$  students.

(4)  The probability can be calculated as the sum of three individual probabilities:

$$ \text{Pr[one field of study] = Pr}( \overline{B} \cap \overline{I} \cap T) + {\rm Pr}( \overline{B} \cap I \cap \overline{T}) + {\rm Pr}( \it B \cap \overline{I} \cap \overline{T}).$$

• Each individual probability corresponds to an area in the Venn diagram and can be determined by addition or subtraction of triangles or rectangles (see graph):

$$p_1 = {\rm Pr}( \overline{B} \cap \overline{I} \cap T) = {\rm Triangle\ (ABC)}= \frac{1}{2}\hspace{0.02cm} \cdot \hspace{0.02cm}\frac{1}{4}\hspace{0.02cm}\cdot \hspace{0.02cm}\frac{1}{4}= \frac{1}{32}\hspace{0.1cm}\underline{\approx 0.0313},$$

$$p_2 ={\rm Pr}( \overline{B} \cap I \cap \overline{T}) = {\rm Rectangle\hspace{0.1cm}(DEFG)}= \frac{1}{4}\hspace{0.02cm}\cdot \hspace{0.02cm} \frac{1}{4}\hspace{0.02cm}+ \hspace{0.02cm}\frac{1}{2}\hspace{0.02cm}\cdot \hspace{0.02cm} \frac{1}{4}\hspace{0.02cm}\cdot \hspace{0.02cm} \frac{1}{4} = \frac{3}{32}\hspace{0.1cm}\underline{\approx 0.0938},$$

$$p_3 = {\rm Pr}( B \cap \overline{I} \cap \overline{T}) ={\rm Rectangle\hspace{0.1cm}(HIJK)}= {\rm Triangle\hspace{0.1cm}(HLK)}- {\rm Triangle\hspace{0.1cm}(ILJ)} = \frac{1}{2}\hspace{0.02cm} \cdot \hspace{0.02cm} \frac{5}{4}\hspace{0.02cm} \cdot \hspace{0.02cm} \frac{5}{8}\hspace{0.02cm} - \hspace{0.02cm}\frac{1}{2}\hspace{0.02cm} \cdot \hspace{0.02cm} \frac{1}{4} \cdot \frac{1}{4} = \frac{23}{64}\hspace{0.1cm}\underline{\approx 0.3594}.$$

 $\text{Or:}\hspace{0.3cm}$

$$p_3 = {\rm Triangle\hspace{0.1cm}(HIC)}- {\rm Triangle\hspace{0.1cm}(KJC)} ={1}/{2}\hspace{0.1cm} \cdot \hspace{0.1cm} 1 \hspace{0.1cm} \cdot \hspace{0.1cm} 1 \hspace{0.1cm} - \hspace{0.1cm}{1}/{2}\hspace{0.05cm} \cdot \hspace{0.1cm} {3}/{4} \cdot {3}/{8} = {23}/{64}.$$

• The sum of these three probabilities leads to the final result  $ \text{Pr[one field of study] } = 31/64 \;\underline {\approx 48.43 \%}$.

(5)  This probability is expressed by the triangle  $\text{Triangle(AGK)}$ .  This has the area

$$\rm Pr[three fields of study] = {1}/{2}\cdot {1}/{4}\cdot {1}/{8} = {1}/{64}\hspace{0.15cm}\underline{\approx 1.56 \%}.$$

(6)  The three events

• "only one field of study",
• "two fields of study" and
• "three fields of study"

form a complete system.  Thus, using the results of the last subtasks, we obtain:

$$\rm Pr[two fields of study] = 1- \text{Pr[one field of study] } - \rm Pr[three fields of study]= 1- {31}/{64} - {1}/{64} \hspace{0.15cm}\underline{= 50\%}.$$

One would arrive at exactly the same result – but with considerably more effort – in the direct way accordingly:

$${\rm Pr[two fields of study] = Pr}(B\cap I \cap\overline{T}) + {\rm Pr}(B\cap\overline{I}\cap{T}) + {\rm Pr}(\overline{B}\cap I \cap T).$$