Difference between revisions of "Theory of Stochastic Signals/Statistical Dependence and Independence"
| Line 92: | Line 92: | ||
| − | == | + | ==General multiplication theorem== |
<br> | <br> | ||
| − | + | We consider several events denoted as $A_i$ with $1 ≤ i ≤ I$ . However, these events $A_i$ now no longer represent a [[Theory_of_Stochastic_Signals/Set_Theory_Basics#Complete_system|complete system]] , viz, | |
| − | * | + | *they are not pairwise disjoint to each other, and |
| − | * | + | *there may also be statistical ties between the individual events. |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
$\text{Definition:}$ | $\text{Definition:}$ | ||
| − | + | For the so-called '''joint probability''', i.e. for the probability of the intersection of al $I$ events $A_i$, holds in this case: | |
:$${\rm Pr}(A_{\rm 1} \cap \hspace{0.02cm}\text{ ...}\hspace{0.1cm} \cap A_{I}) = | :$${\rm Pr}(A_{\rm 1} \cap \hspace{0.02cm}\text{ ...}\hspace{0.1cm} \cap A_{I}) = | ||
{\rm Pr}(A_{I})\hspace{0.05cm}\cdot\hspace{0.05cm}{\rm Pr}(A_{I \rm -1} \hspace{0.05cm}\vert \hspace{0.05cm} A_I) \hspace{0.05cm}\cdot \hspace{0.05cm}{\rm Pr}(A_{I \rm -2} \hspace{0.05cm}\vert\hspace{0.05cm} A_{I - \rm 1}\cap A_I)\hspace{0.05cm} \cdot \hspace{0.02cm}\text{ ...} \hspace{0.1cm} \cdot\hspace{0.05cm} {\rm Pr}(A_{\rm 1} \hspace{0.05cm}\vert \hspace{0.05cm}A_{\rm 2} \cap \hspace{0.02cm}\text{ ...} \hspace{0.1cm}\cap A_{ I}).$$ | {\rm Pr}(A_{I})\hspace{0.05cm}\cdot\hspace{0.05cm}{\rm Pr}(A_{I \rm -1} \hspace{0.05cm}\vert \hspace{0.05cm} A_I) \hspace{0.05cm}\cdot \hspace{0.05cm}{\rm Pr}(A_{I \rm -2} \hspace{0.05cm}\vert\hspace{0.05cm} A_{I - \rm 1}\cap A_I)\hspace{0.05cm} \cdot \hspace{0.02cm}\text{ ...} \hspace{0.1cm} \cdot\hspace{0.05cm} {\rm Pr}(A_{\rm 1} \hspace{0.05cm}\vert \hspace{0.05cm}A_{\rm 2} \cap \hspace{0.02cm}\text{ ...} \hspace{0.1cm}\cap A_{ I}).$$ | ||
| − | In | + | In the same way, of course, holds: |
:$${\rm Pr}(A_{\rm 1} \cap \hspace{0.02cm}\text{ ...}\hspace{0.1cm} \cap A_{I}) = {\rm Pr}(A_1)\hspace{0.05cm}\cdot\hspace{0.05cm}{\rm Pr}(A_2 \hspace{0.05cm}\vert \hspace{0.05cm} A_1) \hspace{0.05cm}\cdot \hspace{0.05cm}{\rm Pr}(A_3 \hspace{0.05cm}\vert \hspace{0.05cm} A_1\cap A_2)\hspace{0.05cm} \cdot \hspace{0.02cm}\text{ ...}\hspace{0.1cm} \cdot\hspace{0.05cm} {\rm Pr}(A_I \hspace{0.05cm}\vert \hspace{0.05cm}A_1 \cap \hspace{0.02cm} \text{ ...} \hspace{0.1cm}\cap A_{ I-1}).$$}} | :$${\rm Pr}(A_{\rm 1} \cap \hspace{0.02cm}\text{ ...}\hspace{0.1cm} \cap A_{I}) = {\rm Pr}(A_1)\hspace{0.05cm}\cdot\hspace{0.05cm}{\rm Pr}(A_2 \hspace{0.05cm}\vert \hspace{0.05cm} A_1) \hspace{0.05cm}\cdot \hspace{0.05cm}{\rm Pr}(A_3 \hspace{0.05cm}\vert \hspace{0.05cm} A_1\cap A_2)\hspace{0.05cm} \cdot \hspace{0.02cm}\text{ ...}\hspace{0.1cm} \cdot\hspace{0.05cm} {\rm Pr}(A_I \hspace{0.05cm}\vert \hspace{0.05cm}A_1 \cap \hspace{0.02cm} \text{ ...} \hspace{0.1cm}\cap A_{ I-1}).$$}} | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 3:}$ |
| − | + | A lottery drum contains ten lots, including three hits $($event $T_1)$. Then the probability of drawing two hits with two tickets is: | |
:$${\rm Pr}(T_1 \cap T_2) = {\rm Pr}(T_1) \cdot {\rm Pr}(T_2 \hspace{0.05cm }\vert \hspace{0.05cm} T_1) = 3/10 \cdot 2/9 = 1/15 \approx 6.7 \%.$$ | :$${\rm Pr}(T_1 \cap T_2) = {\rm Pr}(T_1) \cdot {\rm Pr}(T_2 \hspace{0.05cm }\vert \hspace{0.05cm} T_1) = 3/10 \cdot 2/9 = 1/15 \approx 6.7 \%.$$ | ||
| − | * | + | *This takes into account that in the second draw $($event $T_2)$ there would be only nine tickets and two hits in the urn if one hit had been drawn in the first run ⇒ ${\rm Pr}(T_2 \hspace{0.05cm} \vert\hspace{0.05cm} T_1) = 2/9$ . |
| − | * | + | *However, if the tickets were returned to the drum after the draw, the events $T_1$ and $T_2$ would be statistically independent and it would hold: |
:$$ {\rm Pr}(T_1 ∩ T_2) = (3/10)^2 = 9\%.$$}} | :$$ {\rm Pr}(T_1 ∩ T_2) = (3/10)^2 = 9\%.$$}} | ||
| − | == | + | ==Inference probability== |
<br> | <br> | ||
| − | + | Given again events $A_i$ with $1 ≤ i ≤ I$, that form a complete system. That is: | |
| − | * | + | *All events are pairwise disjoint $(A_i ∩ A_j = ϕ$ for all $i ≠ j$ ). |
| − | * | + | *The union gives the universal set: |
:$$\rm \bigcup_{\it i=1}^{\it I}\it A_i = \it G.$$ | :$$\rm \bigcup_{\it i=1}^{\it I}\it A_i = \it G.$$ | ||
| − | + | Besides, we consider the event $B$, of which all conditional probabilities ${\rm Pr}(B \hspace{0.05cm} | \hspace{0.05cm} A_i)$ with indices $1 ≤ i ≤ I$ are known. | |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{ | + | $\text{Theorem of total probability:}$ |
| − | + | Under the above conditions, the (unconditional) probability of event $B$ is: | |
:$${\rm Pr}(B) = \sum_{i={\rm1} }^{I}{\rm Pr}(B \cap A_i) = \sum_{i={\rm1} }^{I}{\rm Pr}(B \hspace{0.05cm} \vert\hspace{0.05cm} A_i)\cdot{\rm Pr}(A_i).$$}} | :$${\rm Pr}(B) = \sum_{i={\rm1} }^{I}{\rm Pr}(B \cap A_i) = \sum_{i={\rm1} }^{I}{\rm Pr}(B \hspace{0.05cm} \vert\hspace{0.05cm} A_i)\cdot{\rm Pr}(A_i).$$}} | ||
| Line 136: | Line 136: | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
$\text{Definition:}$ | $\text{Definition:}$ | ||
| − | + | From this equation, using [[Theory_of_Stochastic_Signals/Statistical_Dependence_and_Independence#Conditional_Probability|Bayes' theorem]] for '''Inference probability''': | |
:$${\rm Pr}(A_i \hspace{0.05cm} \vert \hspace{0.05cm} B) = \frac{ {\rm Pr}( B \mid A_i)\cdot {\rm Pr}(A_i )}{ {\rm Pr}(B)} = \frac{ {\rm Pr}(B \hspace{0.05cm} \vert \hspace{0.05cm} A_i)\cdot {\rm Pr}(A_i )}{\sum_{k={\rm1} }^{I}{\rm Pr}(B \hspace{0.05cm} \vert \hspace{0.05cm} A_k)\cdot{\rm Pr}(A_k) }.$$}} | :$${\rm Pr}(A_i \hspace{0.05cm} \vert \hspace{0.05cm} B) = \frac{ {\rm Pr}( B \mid A_i)\cdot {\rm Pr}(A_i )}{ {\rm Pr}(B)} = \frac{ {\rm Pr}(B \hspace{0.05cm} \vert \hspace{0.05cm} A_i)\cdot {\rm Pr}(A_i )}{\sum_{k={\rm1} }^{I}{\rm Pr}(B \hspace{0.05cm} \vert \hspace{0.05cm} A_k)\cdot{\rm Pr}(A_k) }.$$}} | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 4:}$ |
| − | + | Munich's student dorms are occupied by students from | |
| − | * | + | *the Ludwig Maximilian Universiy of Munich $($event $L$ ⇒ ${\rm Pr}(L) = 70\%)$ and |
| − | * | + | *the Technical University of Munich $($event $T$ ⇒ ${\rm Pr}(T) = 30\%)$. |
| − | + | It is further known that at LMU $60\%$ of all students are female, whereas at TUM only $10\%$ are female. | |
| − | * | + | *The proportion of all female students in the dormitory $($event $W)$ can then be determined using the total probability theorem: |
:$${\rm Pr}(W) = {\rm Pr}(W \hspace{0.05cm} \vert \hspace{0.05cm} L)\hspace{0.01cm}\cdot\hspace{0.01cm}{\rm Pr}(L) \hspace{0.05cm}+\hspace{0.05cm} {\rm Pr}(W \hspace{0.05cm} \vert \hspace{0.05cm} T)\hspace{0.01cm}\cdot\hspace{0.01cm}{\rm Pr}(T) = \rm 0.6\hspace{0.01cm}\cdot\hspace{0.01cm}0.7\hspace{0.05cm}+\hspace{0.05cm}0.1\hspace{0.01cm}\cdot \hspace{0.01cm}0.3 = 45 \%.$$ | :$${\rm Pr}(W) = {\rm Pr}(W \hspace{0.05cm} \vert \hspace{0.05cm} L)\hspace{0.01cm}\cdot\hspace{0.01cm}{\rm Pr}(L) \hspace{0.05cm}+\hspace{0.05cm} {\rm Pr}(W \hspace{0.05cm} \vert \hspace{0.05cm} T)\hspace{0.01cm}\cdot\hspace{0.01cm}{\rm Pr}(T) = \rm 0.6\hspace{0.01cm}\cdot\hspace{0.01cm}0.7\hspace{0.05cm}+\hspace{0.05cm}0.1\hspace{0.01cm}\cdot \hspace{0.01cm}0.3 = 45 \%.$$ | ||
| − | * | + | *If we meet a female student, we can use the inference probability |
:$${\rm Pr}(L \hspace{-0.05cm}\mid \hspace{-0.05cm}W) = \frac{ {\rm Pr}(W \hspace{-0.05cm}\mid \hspace{-0.05cm}L)\cdot {\rm Pr}(L) }{ {\rm Pr}(W \hspace{-0.05cm}\mid \hspace{-0.05cm}L) \cdot {\rm Pr}(L) +{\rm Pr}(W \hspace{-0.05cm}\mid \hspace{-0.05cm}T) \cdot {\rm Pr}(T)}=\rm \frac{0.6\cdot 0.7}{0.6\cdot 0.7 + 0.1\cdot 0.3}=\frac{14}{15}\approx 93.3 \%$$ | :$${\rm Pr}(L \hspace{-0.05cm}\mid \hspace{-0.05cm}W) = \frac{ {\rm Pr}(W \hspace{-0.05cm}\mid \hspace{-0.05cm}L)\cdot {\rm Pr}(L) }{ {\rm Pr}(W \hspace{-0.05cm}\mid \hspace{-0.05cm}L) \cdot {\rm Pr}(L) +{\rm Pr}(W \hspace{-0.05cm}\mid \hspace{-0.05cm}T) \cdot {\rm Pr}(T)}=\rm \frac{0.6\cdot 0.7}{0.6\cdot 0.7 + 0.1\cdot 0.3}=\frac{14}{15}\approx 93.3 \%$$ | ||
| − | : | + | :predict that she will study at LMU. A quite realistic result (at least in the past).}} |
| − | + | The topic of this chapter is illustrated with examples in the (German language) learning video | |
| + | :[[Statistische_Abhängigkeit_und_Unabhängigkeit_(Lernvideo)|Statistische Abhängigkeit und Unabhängigkeit]] $\Rightarrow$ "Statistical Dependence and Independence.". | ||
| − | == | + | ==Exercises for the chapter== |
<br> | <br> | ||
[[Aufgaben:1.4_2S/3E-Kanalmodell|Aufgabe 1.4: 2S/3E-Kanalmodell]] | [[Aufgaben:1.4_2S/3E-Kanalmodell|Aufgabe 1.4: 2S/3E-Kanalmodell]] | ||
Revision as of 20:34, 28 November 2021
Contents
General Definition of Statistical Dependence
So far we have not paid much attention to statistical dependence between events, even though we have already used it as in the case of two disjoint sets: If an element belongs to $A$, it cannot with certainty also be contained in the disjoint set $B$ .
The strongest form of dependence at all is such a deterministic dependence between two sets or two events. Less pronounced is the statistical dependence. Let us start with its complement:
$\text{Definition:}$ Two events $A$ and $B$ are called statistically independent , if the probability of the intersection $A ∩ B$ is equal to the product of the individual probabilities:
- $${\rm Pr}(A \cap B) = {\rm Pr}(A)\cdot {\rm Pr}(B).$$
- In some applications, statistical independence is obvious, for example, in the "coin toss" experiment. The probability for "heads" or "tails" is independent of whether heads oder tails occurred in the last toss.
- And also the individual results in the random experiment "throwing a roulette ball" are always statistically independent of each other under fair conditions, even if individual system players do not want to admit this.
- In other applications, on the other hand, the question whether two events are statistically independent or not is not or only very difficult to answer instinctively. Here one can only arrive at the correct answer by checking the formal independence criterion given above, as the following example will show.
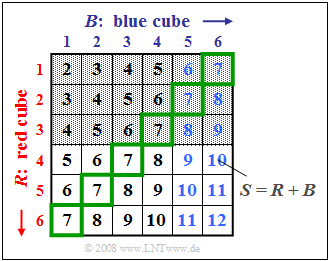
$\text{Example 1:}$ We consider the experiment "throwing two dice", where the two dice can be distinguished by their colors red $(R)$ and blue $(B)$ .
The graph illustrates this fact, where the sum $S = R + B$ is entered in the two-dimensional field $(R, B)$ .
For the following description we define the following events:
- $A_1$: The number of eyes of the red die is $R < 4$ (red background) ⇒ ${\rm Pr}(A_1) = 1/2$,
- $A_2$: The number of eyes of the blue die is $B > 4$ (blue font) ⇒ ${\rm Pr}(A_2) = 1/3$,
- $A_3$: The sum of the two dice is $S = 7$ (green outline) ⇒ ${\rm Pr}(A_3) = 1/6$,
- $A_4$: The sum of the two dice is $S = 8$ ⇒ ${\rm Pr}(A_4) = 5/36$,
- $A_5$: The sum of the two dice is $S = 10$ ⇒ ${\rm Pr}(A_5) = 3/36$.
The graph can be interpreted as follows:
- The two events $A_1$ and $A_2$ are statistically independent because the probability ${\rm Pr}(A_1 ∩ A_2) = 1/6$ of the intersection is equal to the product of the two individual probabilities ${\rm Pr}(A_1) = 1/2$ and ${\rm Pr}(A_2) = 1/3$ . Given the problem definition, any other result would also have been very surprising.
- But also the events $A_1$ and $A_3$ are statistically independent because of ${\rm Pr}(A_1) = 1/2$, ${\rm Pr}(A_3) = 1/6$ and ${\rm Pr}(A_1 ∩ A_3) = 1/12$ statistisch unabhängig. The probability of intersection $(1/12)$ arises because three of the $36$ squares are both highlighted in red and outlined in green.
- In contrast, there are statistical ties between events $A_1$ and $A_4$ because the probability of intersection ⇒ ${\rm Pr}(A_1 ∩ A_4) = 1/18 = 4/72$ is not equal to the product ${\rm Pr}(A_1) \cdot {\rm Pr}(A_4)= 1/2 \cdot 5/36 = 5/72$ .
- The two events $A_1$ and $A_5$ are even disjunctive ⇒ ${\rm Pr}(A_1 ∩ A_5) = 0$: none of the boxes with red background is labeled $S=10$ . This example shows that disjunctivity is a particularly pronounced form of statistical dependence.
Conditional Probability
If there are statistical ties between the two events $A$ and $B$ , the (unconditional) probabilities ${\rm Pr}(A)$ and ${\rm Pr}(B)$ do not describe the situation unambiguously in the statistical sense. So-called conditional probabilities are then required.
$\text{Definitions:}$ The conditional probability of $A$ under condition $B$ can be calculated as follows:
- $${\rm Pr}(A\hspace{0.05cm} \vert \hspace{0.05cm} B) = \frac{ {\rm Pr}(A \cap B)}{ {\rm Pr}(B)}.$$
Similarly, the conditional probability of $B$ under condition $A$ is:
- $${\rm Pr}(B\hspace{0.05cm} \vert \hspace{0.05cm}A) = \frac{ {\rm Pr}(A \cap B)}{ {\rm Pr}(A)}.$$
Combining these two equations, we get Bayes' Theorem:
- $${\rm Pr}(B \hspace{0.05cm} \vert \hspace{0.05cm} A) = \frac{ {\rm Pr}(A\hspace{0.05cm} \vert \hspace{0.05cm} B)\cdot {\rm Pr}(B)}{ {\rm Pr}(A)}.$$
Below are some properties of conditional probabilities:
- A conditional probability also always lies between $0$ and $1$ including these two limits: $0 \le {\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm} B) \le 1$.
- If the condition $B$ can be regarded as constant, all calculation rules given in the chapter Set Theory Basics for the unconditional probabilities ${\rm Pr}(A)$ and ${\rm Pr}(B)$ still apply.
- If the existing events $A$ and $B$ are disjoint, then ${\rm Pr}(A\hspace{0.05cm} | \hspace{0.05cm} B) = {\rm Pr}(B\hspace{0.05cm} | \hspace{0.05cm}A)= 0$.
- If $B$ is a real or fake subset of $A$, then ${\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm} B) =1$.
- If two events $A$ and $B$ are statistically independent, their conditional probabilities are equal to the unconditional ones, as the following calculation shows:
- $${\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm} B) = \frac{{\rm Pr}(A \cap B)}{{\rm Pr}(B)} = \frac{{\rm Pr} ( A) \cdot {\rm Pr} ( B)} { {\rm Pr}(B)} = {\rm Pr} ( A).$$
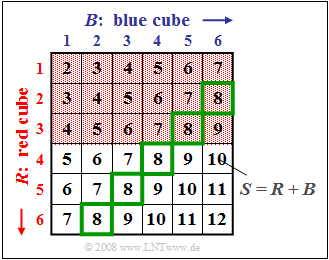
$\text{Example 2:}$ We again consider the experiment "Throwing two dice", where, as in $\text{Example 1}$ $S = R + B$ denotes the sum of the red and blue dice.
Here we consider ties between the two events
- $A_1$: The roll of the red die is $R < 4$ (red background) ⇒ ${\rm Pr}(A_1) = 1/2$,
- $A_4$: The sum of the two dice is $S = 8$ (green outline) ⇒ ${\rm Pr}(A_4) = 5/36$,
and refer again to the event
- $A_3$: The sum of the two cubes is $S = 7$ ⇒ ${\rm Pr}(A_3) = 1/6$.
Regarding this graph, note:
- There are statistical ties between events $A_1$ and $A_4$ , since the probability of intersection ⇒ ${\rm Pr}(A_1 ∩ A_4) = 2/36 = 4/72$ is not equal to the product ${\rm Pr}(A_1) \cdot {\rm Pr}(A_4)= 1/2 \cdot 5/36 = 5/72$ . *The conditional probability ${\rm Pr}(A_1 \hspace{0.05cm} \vert \hspace{0.05cm} A_4) = 2/5$ can be calculated from the quotient of the joint probability ${\rm Pr}(A_1 ∩ A_4) = 2/36$ and the probability ${\rm Pr}(A_4) = 5/36$ .
- Since $A_1$ and $A_4$ are statistically dependent, the conditional probability ${\rm Pr}(A_1 \hspace{0.05cm}\vert \hspace{0.05cm} A_4) = 2/5$ (two of the five squares outlined in green are highlighted in red) is not equal to the absolute probability ${\rm Pr}(A_1) = 1/2$ (half of all squares are highlighted in red).
- Similarly, the conditional probability ${\rm Pr}(A_4 \hspace{0.05cm} \vert \hspace{0.05cm} A_1) = 2/18 = 4/36$ (two of the $18$ fields with a red background are outlined in green) is unequal to the absolute probability ${\rm Pr}(A_4) = 5/36$ (a total of five of the $36$ fields are outlined in green).
- This last result can also be derived using Bayes' theorem , for example:
- $${\rm Pr}(A_4 \hspace{0.05cm} \vert\hspace{0.05cm} A_1) = \frac{ {\rm Pr}(A_1 \hspace{0.05cm} \vert\hspace{0.05cm} A_4)\cdot {\rm Pr} ( A_4)} { {\rm Pr}(A_1)} = \frac{2/5 \cdot 5/36}{1/2} = 1/9.$$
- In contrast, the following conditional probabilities hold for $A_1$ and the statistically independent event $A_3$ , see Example 1:
- $${\rm Pr}(A_{\rm 1} \hspace{0.05cm}\vert \hspace{0.05cm} A_{\rm 3}) = {\rm Pr}(A_{\rm 1}) = \rm 1/2\hspace{0.5cm}{\rm bzw.}\hspace{0.5cm}{\rm Pr}(A_{\rm 3} \hspace{0.05cm} \vert \hspace{0.05cm} A_{\rm 1}) = {\rm Pr}(A_{\rm 3}) = 1/6.$$
General multiplication theorem
We consider several events denoted as $A_i$ with $1 ≤ i ≤ I$ . However, these events $A_i$ now no longer represent a complete system , viz,
- they are not pairwise disjoint to each other, and
- there may also be statistical ties between the individual events.
$\text{Definition:}$ For the so-called joint probability, i.e. for the probability of the intersection of al $I$ events $A_i$, holds in this case:
- $${\rm Pr}(A_{\rm 1} \cap \hspace{0.02cm}\text{ ...}\hspace{0.1cm} \cap A_{I}) = {\rm Pr}(A_{I})\hspace{0.05cm}\cdot\hspace{0.05cm}{\rm Pr}(A_{I \rm -1} \hspace{0.05cm}\vert \hspace{0.05cm} A_I) \hspace{0.05cm}\cdot \hspace{0.05cm}{\rm Pr}(A_{I \rm -2} \hspace{0.05cm}\vert\hspace{0.05cm} A_{I - \rm 1}\cap A_I)\hspace{0.05cm} \cdot \hspace{0.02cm}\text{ ...} \hspace{0.1cm} \cdot\hspace{0.05cm} {\rm Pr}(A_{\rm 1} \hspace{0.05cm}\vert \hspace{0.05cm}A_{\rm 2} \cap \hspace{0.02cm}\text{ ...} \hspace{0.1cm}\cap A_{ I}).$$
In the same way, of course, holds:
- $${\rm Pr}(A_{\rm 1} \cap \hspace{0.02cm}\text{ ...}\hspace{0.1cm} \cap A_{I}) = {\rm Pr}(A_1)\hspace{0.05cm}\cdot\hspace{0.05cm}{\rm Pr}(A_2 \hspace{0.05cm}\vert \hspace{0.05cm} A_1) \hspace{0.05cm}\cdot \hspace{0.05cm}{\rm Pr}(A_3 \hspace{0.05cm}\vert \hspace{0.05cm} A_1\cap A_2)\hspace{0.05cm} \cdot \hspace{0.02cm}\text{ ...}\hspace{0.1cm} \cdot\hspace{0.05cm} {\rm Pr}(A_I \hspace{0.05cm}\vert \hspace{0.05cm}A_1 \cap \hspace{0.02cm} \text{ ...} \hspace{0.1cm}\cap A_{ I-1}).$$
$\text{Example 3:}$ A lottery drum contains ten lots, including three hits $($event $T_1)$. Then the probability of drawing two hits with two tickets is:
- $${\rm Pr}(T_1 \cap T_2) = {\rm Pr}(T_1) \cdot {\rm Pr}(T_2 \hspace{0.05cm }\vert \hspace{0.05cm} T_1) = 3/10 \cdot 2/9 = 1/15 \approx 6.7 \%.$$
- This takes into account that in the second draw $($event $T_2)$ there would be only nine tickets and two hits in the urn if one hit had been drawn in the first run ⇒ ${\rm Pr}(T_2 \hspace{0.05cm} \vert\hspace{0.05cm} T_1) = 2/9$ .
- However, if the tickets were returned to the drum after the draw, the events $T_1$ and $T_2$ would be statistically independent and it would hold:
- $$ {\rm Pr}(T_1 ∩ T_2) = (3/10)^2 = 9\%.$$
Inference probability
Given again events $A_i$ with $1 ≤ i ≤ I$, that form a complete system. That is:
- All events are pairwise disjoint $(A_i ∩ A_j = ϕ$ for all $i ≠ j$ ).
- The union gives the universal set:
- $$\rm \bigcup_{\it i=1}^{\it I}\it A_i = \it G.$$
Besides, we consider the event $B$, of which all conditional probabilities ${\rm Pr}(B \hspace{0.05cm} | \hspace{0.05cm} A_i)$ with indices $1 ≤ i ≤ I$ are known.
$\text{Theorem of total probability:}$ Under the above conditions, the (unconditional) probability of event $B$ is:
- $${\rm Pr}(B) = \sum_{i={\rm1} }^{I}{\rm Pr}(B \cap A_i) = \sum_{i={\rm1} }^{I}{\rm Pr}(B \hspace{0.05cm} \vert\hspace{0.05cm} A_i)\cdot{\rm Pr}(A_i).$$
$\text{Definition:}$ From this equation, using Bayes' theorem for Inference probability:
- $${\rm Pr}(A_i \hspace{0.05cm} \vert \hspace{0.05cm} B) = \frac{ {\rm Pr}( B \mid A_i)\cdot {\rm Pr}(A_i )}{ {\rm Pr}(B)} = \frac{ {\rm Pr}(B \hspace{0.05cm} \vert \hspace{0.05cm} A_i)\cdot {\rm Pr}(A_i )}{\sum_{k={\rm1} }^{I}{\rm Pr}(B \hspace{0.05cm} \vert \hspace{0.05cm} A_k)\cdot{\rm Pr}(A_k) }.$$
$\text{Example 4:}$ Munich's student dorms are occupied by students from
- the Ludwig Maximilian Universiy of Munich $($event $L$ ⇒ ${\rm Pr}(L) = 70\%)$ and
- the Technical University of Munich $($event $T$ ⇒ ${\rm Pr}(T) = 30\%)$.
It is further known that at LMU $60\%$ of all students are female, whereas at TUM only $10\%$ are female.
- The proportion of all female students in the dormitory $($event $W)$ can then be determined using the total probability theorem:
- $${\rm Pr}(W) = {\rm Pr}(W \hspace{0.05cm} \vert \hspace{0.05cm} L)\hspace{0.01cm}\cdot\hspace{0.01cm}{\rm Pr}(L) \hspace{0.05cm}+\hspace{0.05cm} {\rm Pr}(W \hspace{0.05cm} \vert \hspace{0.05cm} T)\hspace{0.01cm}\cdot\hspace{0.01cm}{\rm Pr}(T) = \rm 0.6\hspace{0.01cm}\cdot\hspace{0.01cm}0.7\hspace{0.05cm}+\hspace{0.05cm}0.1\hspace{0.01cm}\cdot \hspace{0.01cm}0.3 = 45 \%.$$
- If we meet a female student, we can use the inference probability
- $${\rm Pr}(L \hspace{-0.05cm}\mid \hspace{-0.05cm}W) = \frac{ {\rm Pr}(W \hspace{-0.05cm}\mid \hspace{-0.05cm}L)\cdot {\rm Pr}(L) }{ {\rm Pr}(W \hspace{-0.05cm}\mid \hspace{-0.05cm}L) \cdot {\rm Pr}(L) +{\rm Pr}(W \hspace{-0.05cm}\mid \hspace{-0.05cm}T) \cdot {\rm Pr}(T)}=\rm \frac{0.6\cdot 0.7}{0.6\cdot 0.7 + 0.1\cdot 0.3}=\frac{14}{15}\approx 93.3 \%$$
- predict that she will study at LMU. A quite realistic result (at least in the past).
The topic of this chapter is illustrated with examples in the (German language) learning video
- Statistische Abhängigkeit und Unabhängigkeit $\Rightarrow$ "Statistical Dependence and Independence.".
Exercises for the chapter
Aufgabe 1.4: 2S/3E-Kanalmodell
Aufgabe 1.4Z: Summe von Ternärgrößen
Aufgabe 1.5Z: Ausfallwahrscheinlichkeiten