Difference between revisions of "Aufgaben:Exercise 5.1: Sampling Theorem"
(Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=*Buch*/*Kapitel* }} 250px|right|* ===Fragebogen=== <quiz display=simple> {Multiple-Choice Frage |type="[]"} - Falsch +…“) |
|||
| Line 3: | Line 3: | ||
}} | }} | ||
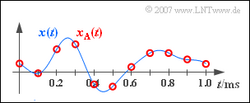
| − | [[File: | + | [[File:P_ID1126__Sig_A_5_1.png|250px|right|Abtasttheorem (Aufgabe A5.1)]] |
| + | Gegeben ist ein Analogsignal x(t) entsprechend der Skizze. Bekannt ist, dass dieses Signal keine höheren Frequenzen als BNF = 4 kHz beinhaltet. Durch Abtastung (Abtastrate fA) erhält man das in der Grafik rot eingezeichnete Signal xA(t). | ||
| + | Zur Signalrekonstruktion wird ein Tiefpass mit dem Frequenzgang | ||
| + | |||
| + | $$H(f) = \left\{ \begin{array}{c} 1 \\ | ||
| + | 0 \\ \end{array} \right.\quad | ||
| + | \begin{array}{*{5}c} {\rm{{\rm{f\ddot{u}r}}}} | ||
| + | \\ {\rm{{\rm{f\ddot{u}r}}}} \\ \end{array}\begin{array}{*{5}c} | ||
| + | |f| < f_1 \hspace{0.05cm}, \\ | ||
| + | |f| > f_2 \hspace{0.05cm} \\ | ||
| + | \end{array}$$ | ||
| + | eingesetzt. Der Bereich zwischen den Frequenzen f1 und f2 > f1 ist für die Lösung dieser Aufgabe nicht relevant. | ||
| + | Die Eckfrequenzen f1 und f2 sind so zu bestimmen, dass das Ausgangssignal y(t) des Tiefpasses mit dem Signal x(t) exakt übereinstimmt. | ||
| + | Hinweis: Die Aufgabe bezieht sich auf die theoretischen Grundlagen von Kapitel 5.1. Zu der hier behandelten Thematik gibt es auch ein Interaktionsmodul: | ||
| + | Abtastung periodischer Signale und Signalrekonstruktion | ||
===Fragebogen=== | ===Fragebogen=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Ermitteln Sie aus der Grafik die zugrundeliegende Abtastrate. |
| + | |type="{}"} | ||
| + | $f_A=$ { 10 } kHz | ||
| + | |||
| + | {Bei welchen Frequenzen besitzt XA(f) mit Sicherheit keine Anteile? | ||
|type="[]"} | |type="[]"} | ||
| − | - | + | - $f= $ { 2.5 } kHz |
| − | + | + | + $f= $ { 5.5 } kHz |
| + | - $f= $ { 6.5 } kHz | ||
| + | + $f= $ { 34.5 } kHz | ||
| + | {Bis zu welcher Eckfrequenz f1 wird das Signal perfekt rekonstruiert? | ||
| + | |type="{}"} | ||
| + | $f_{1,\text{min}}=$ { 4 } kHz | ||
| − | { | + | {Bis zu welcher Eckfrequenz f2 wird das Signal perfekt rekonstruiert? |
|type="{}"} | |type="{}"} | ||
| − | + | $f_{2,\text{min}}=$ { 6 } kHz | |
| − | |||
| − | |||
</quiz> | </quiz> | ||
| Line 25: | Line 46: | ||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1.''' | + | '''1.''' a) Der Abstand zweier benachbarter Abtastwerte beträgt TA = 0.1 ms. Somit erhält man für die Abtastrate fA = 1/TA = 10 kHz. |
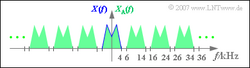
| + | b) Das Spektrum XA(f) des abgetasteten Signals erhält man aus X(f) durch periodische Fortsetzung im Abstand fA = 10 kHz. Aus der Skizze erkennt man, dass XA(f) durchaus Anteile bei f = 2.5 kHz und f = 6.5 kHz besitzen kann, nicht jedoch bei f = 5.5 kHz. Auch bei f = 34.5 kHz wird XA(f) = 0 gelten. Richtig sind also die Lösungsvorschläge 2 und 4. | ||
| + | |||
| + | [[File:P_ID1127__Sig_A_5_1_b.png|250px|right|Zum Abtasttheorem (ML zu Aufgabe A5.1)]] | ||
| + | |||
| + | c) Es muss sichergestellt sein, dass alle Frequenzen des Analogsignals mit H(f) = 1 bewertet werden. Daraus folgt (siehe Skizze): f1, min = BNF = 4 kHz. | ||
| + | d) Ebenso muss garantiert werden, dass alle Spektralanteile von XA(f), die in X(f) nicht enthalten sind, durch den Tiefpass entfernt werden. Entsprechend der Skizze gilt f2, max = fA – BNF = 6 kHz. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
__NOEDITSECTION__ | __NOEDITSECTION__ | ||
[[Category:Aufgaben zu Signaldarstellung|^4. Bandpassartige Signale^]] | [[Category:Aufgaben zu Signaldarstellung|^4. Bandpassartige Signale^]] | ||
Revision as of 13:19, 19 April 2016
Gegeben ist ein Analogsignal x(t) entsprechend der Skizze. Bekannt ist, dass dieses Signal keine höheren Frequenzen als BNF = 4 kHz beinhaltet. Durch Abtastung (Abtastrate fA) erhält man das in der Grafik rot eingezeichnete Signal xA(t). Zur Signalrekonstruktion wird ein Tiefpass mit dem Frequenzgang
$$H(f) = \left\{ \begin{array}{c} 1 \\ 0 \\ \end{array} \right.\quad \begin{array}{*{5}c} {\rm{{\rm{f\ddot{u}r}}}} \\ {\rm{{\rm{f\ddot{u}r}}}} \\ \end{array}\begin{array}{*{5}c} |f| < f_1 \hspace{0.05cm}, \\ |f| > f_2 \hspace{0.05cm} \\ \end{array}$$
eingesetzt. Der Bereich zwischen den Frequenzen f1 und f2 > f1 ist für die Lösung dieser Aufgabe nicht relevant. Die Eckfrequenzen f1 und f2 sind so zu bestimmen, dass das Ausgangssignal y(t) des Tiefpasses mit dem Signal x(t) exakt übereinstimmt. Hinweis: Die Aufgabe bezieht sich auf die theoretischen Grundlagen von Kapitel 5.1. Zu der hier behandelten Thematik gibt es auch ein Interaktionsmodul: Abtastung periodischer Signale und Signalrekonstruktion
Fragebogen
Musterlösung
c) Es muss sichergestellt sein, dass alle Frequenzen des Analogsignals mit H(f) = 1 bewertet werden. Daraus folgt (siehe Skizze): f1, min = BNF = 4 kHz. d) Ebenso muss garantiert werden, dass alle Spektralanteile von XA(f), die in X(f) nicht enthalten sind, durch den Tiefpass entfernt werden. Entsprechend der Skizze gilt f2, max = fA – BNF = 6 kHz.