Aufgaben:Exercise 5.5Z: About the Rake Receiver

• Return to book

2-way channel
& rake receiver KORREKTUR: two-way channel, rake receiver

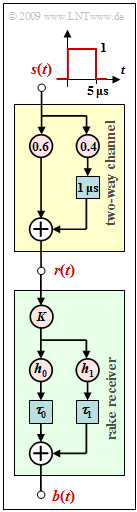
The diagram shows a two-way channel  (yellow background).  The corresponding descriptive equation is:

$$ r(t) =0.6 \cdot s(t) + 0.4 \cdot s (t - \tau) \hspace{0.05cm}.$$

Let the delay on the secondary path be  $τ = 1 \ \rm µ s$. 

Drawn below is the structure of a rake receiver  (green background)  with general coefficients  $K$,  $h_0$,  $h_1$,  $τ_0$  and  $τ_1$.

• The purpose of the rake receiver is to combine the energy of the two signal paths,  making the decision more reliable. 

• The combined impulse response of the channel  (German:  "Kanal"   ⇒   subscript "K")  and the rake receiver can be expressed in the form

$$h_{\rm KR}(t) = A_0 \cdot \delta (t ) + A_1 \cdot \delta (t - \tau) + A_2 \cdot \delta (t - 2\tau)$$

but only if the rake coefficients  $h_0$,  $h_1$,  $τ_0$  and  $τ_1$  are appropriately chosen. 

• The main part of  $h_{\rm KR}(t)$  is supposed to be at  $t = τ$. 
• The constant  $K$  is to be chosen so that the amplitude of the main path  $A_1 = 1$ :

$$K= \frac{1}{h_0^2 + h_1^2}.$$

Apart from the rake parameters,  the signals  $r(t)$  and  $b(t)$ are sought when $s(t)$  is a rectangle of height  $s_0 = 1$  and width  $T = \ \rm 5 µ s$. 

Notes:

• The exercise belongs to the chapter  Error Probability of Direct-Sequence Spread Spectrum Modulation.
• Reference is made in particular to the section  Principle of the rake receiver.

Questions

1

Which statements are valid for the channel impulse response  $h_{\rm K}(t)$?

	$h_{\rm K}(t)$  consists of two Dirac delta functions.
	$h_{\rm K}(t)$  is complex-valued.
	$h_{\rm K}(t)$  is a function periodic with delay time  $\tau$.

2

Which statements are true for the channel frequency response  $H_{\rm K}(f)$?

	$H_{\rm K}(f = 0) = 2$  is true.
	$H_{\rm K}(f)$  is complex-valued.
	$|H_{\rm K}(f)|$  is a function periodic with frequency  $1/τ$.

3

Set  $K = 1$,  $h_0 = 0.6$  and  $h_1 = 0.4$.  Determine the delays  $τ_0$  and  $τ_1$ so that the  $h_{\rm KR}(t)$ equation is satisfied with  $A_0 = A_2$. 

$τ_0 \ = \ $ $\ \rm µ s$

$τ_1 \ = \ $ $\ \rm µ s$

4

What value should be chosen for the constant  $K$? 

$K \ = \ $

5

Which statements are valid for the signals  $r(t)$  and  $b(t)$?

	The maximum value of  $r(t)$  is  $1$.
	The width of  $r(t)$  is  $7 \ µ s$.
	The maximum value of  $b(t)$  is  $1$.
	The width of  $b(t)$  is  $7 \ µ s$.

Solution

Solution

(1)  Solution 1 is correct:

• The impulse response  $h_{\rm K}(t)$  is obtained as the received signal  $r(t)$  when there is a Dirac delta pulse at the input   ⇒   $s(t) = δ(t)$.  It follows that:

$$ h_{\rm K}(t) = 0.6 \cdot \delta (t ) + 0.4 \cdot \delta (t - \tau) \hspace{0.05cm}.$$

(2)  Solutions 2 and 3  are correct:

• By definition,  the channel frequency response  $H_{\rm K}(f)$  is the Fourier transform of the impulse response  $h_{\rm K}(t)$.  With the shift theorem this results in:

$$H_{\rm K}(f) = 0.6 + 0.4 \cdot {\rm e}^{ \hspace{0.03cm}{\rm j} \hspace{0.03cm} \cdot \hspace{0.03cm}2 \pi f \tau}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} H_{\rm K}(f= 0) = 0.6 + 0.4 = 1 \hspace{0.05cm}.$$

• Accordingly,  the first proposed solution is incorrect in contrast to the other two:

1.   $H_{\rm K}(f)$ is complex-valued and
2.  the magnitude is periodic with  $1/τ$,  as the following calculation shows:

$$|H_{\rm K}(f)|^2 = \left [0.6 + 0.4 \cdot \cos(2 \pi f \tau) \right ]^2 + \left [ 0.4 \cdot \sin(2 \pi f \tau) \right ]^2 = \left [0.6^2 + 0.4^2 \cdot \left ( \cos^2(2 \pi f \tau) + \sin^2(2 \pi f \tau)\right ) \right ] + 2 \cdot 0.6 \cdot 0.4 \cdot \cos(2 \pi f \tau).$$

• For  $f = 0$,   $|H_{\rm K}(f)| = 1$.  This value is repeated in the respective frequency spacing  $1/τ$. 

(3)  We first set  $K = 1$ as agreed.

• Altogether we get from  $s(t)$  to the output signal  $b(t)$ via four paths.
• To satisfy the given  $h_{\rm KR}(t)$ equation, either  $τ_0 = 0$  must hold or  $τ_1 = 0$.  With  $τ_0 = 0$  we obtain for the impulse response:

$$h_{\rm KR}(t) = 0.6 \cdot h_0 \cdot \delta (t ) + 0.4 \cdot h_0 \cdot \delta (t - \tau) + 0.6 \cdot h_1 \cdot \delta (t -\tau_1) + 0.4 \cdot h_1 \cdot \delta (t - \tau-\tau_1) \hspace{0.05cm}.$$

• To be able to focus the  "main energy"  at a certain time point,  $τ_1 = τ$  would have to be chosen. 
• With  $h_0 = 0.6$  and  $h_1 = 0.4$,  we then obtain  $A_0 ≠ A_2$:

$$h_{\rm KR}(t) = 0.36 \cdot \delta (t ) +0.48 \cdot \delta (t - \tau) + 0.16 \cdot \delta (t - 2\tau)\hspace{0.05cm}.$$

• In contrast, with  $h_0 = 0.6$,  $h_1 = 0.4$,  $τ_0 = τ$  and  $τ_1 = 0$:

$$h_{\rm KR}(t) = 0.6 \cdot h_0 \cdot \delta (t - \tau ) + 0.4 \cdot h_0 \cdot \delta (t - 2\tau) + 0.6 \cdot h_1 \cdot \delta (t) + 0.4 \cdot h_1 \cdot \delta (t - \tau)= 0.24 \cdot \delta (t ) +0.52 \cdot \delta (t - \tau) + 0.24 \cdot \delta (t - 2\tau) \hspace{0.05cm}.$$

• Here,  the additional condition  $A_0 = A_2$  is satisfied.  Thus,  the result we are looking for is:

$$ \underline{\tau_0 = \tau = 1\,{\rm µ s} \hspace{0.05cm},\hspace{0.2cm}\tau_1 =0} \hspace{0.05cm}.$$

(4)  The following must apply to the normalization factor:

$$K= \frac{1}{h_0^2 + h_1^2} = \frac{1}{0.6^2 + 0.4^2} = \frac{1}{0.52} \hspace{0.15cm}\underline {\approx 1.923} \hspace{0.05cm}.$$

• This gives for the common impulse response  $($it holds  $0.24/0.52 = 6/13)$:

$$ h_{\rm KR}(t) = \frac{6}{13} \cdot \delta (t ) + 1.00 \cdot \delta (t - \tau) + \frac{6}{13} \cdot \delta (t - 2\tau)\hspace{0.05cm}.$$

Signals to illustrate the rake receiver

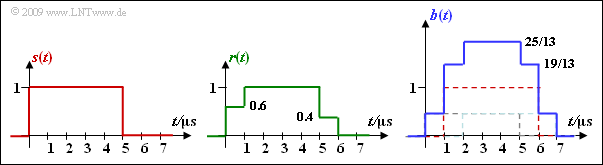
(5)  Statements 1 and 4 are correct, as shown in the diagram:

• For the received signal  $r(t)$  holds:

$$r(t) = 0.6 \cdot s(t) + 0.4 \cdot s (t - 1\,{\rm µ s})\hspace{0.05cm},$$

• and for the rake output signal  $b(t)$:

$$b(t) = \frac{6}{13} \cdot s(t) + 1 \cdot s (t - 1\,{\rm µ s}) + \frac{6}{13} \cdot s (t - 2\,{\rm µ s}) \hspace{0.05cm}.$$

• The overshoot of the output signal   ⇒   $b(t) > 1$  is due to the normalization factor  $K = 25/13$. 
• With  $K = 1$,  the maximum value of  $b(t)$  would actually be  $1$.