Difference between revisions of "Aufgaben:Exercise 4.4: Pointer Diagram for DSB-AM"
| Line 5: | Line 5: | ||
[[File:P_ID718__Sig_A_4_4.png|250px|right|Zeigerdiagramm bei ZSB-AM (Aufgabe A4.4)]] | [[File:P_ID718__Sig_A_4_4.png|250px|right|Zeigerdiagramm bei ZSB-AM (Aufgabe A4.4)]] | ||
| − | Wir gehen von einem cosinusförmigen Quellensignal q(t) mit der Amplitude | + | Wir gehen von einem cosinusförmigen Quellensignal $q(t)$ mit der Amplitude $A_N$ = 0.8 V und der Frequenz $f_N$ = 10 kHz aus. Die Frequenzumsetzung erfolgt mittels Zweiseitenband–Amplitudenmodulation mit Träger, abgekürzt ZSB–AM. |
| − | Das modulierte Signal s(t) lautet mit dem (normierten) Träger z(t) = cos( | + | Das modulierte Signal $s(t)$ lautet mit dem (normierten) Träger $z(t) = \text{cos}(\omega T \dot t)$ und dem Gleichanteil $q_0$ = 1 V: |
| − | $$s(t) & = | + | $$\begin{align*} s(t) & = \left(q_0 + q(t)\right) \cdot z(t)= \left({\rm 1 \hspace{0.05cm} |
V} + {\rm 0.8 \hspace{0.05cm}V}\cdot {\cos} ( \omega_{\rm N}\cdot t)\right) | V} + {\rm 0.8 \hspace{0.05cm}V}\cdot {\cos} ( \omega_{\rm N}\cdot t)\right) | ||
| − | \cdot {\cos} ( \omega_{\rm T}\cdot t) = \\ & = | + | \cdot {\cos} ( \omega_{\rm T}\cdot t) = \\ & = q_0 \cdot {\cos} ( \omega_{\rm T}\cdot t) + |
\frac{A_{\rm N}}{2} \cdot {\cos} ( (\omega_{\rm T}+ \omega_{\rm N}) \cdot t) | \frac{A_{\rm N}}{2} \cdot {\cos} ( (\omega_{\rm T}+ \omega_{\rm N}) \cdot t) | ||
| − | + \frac{A_{\rm N}}{2} \cdot {\cos} ( (\omega_{\rm T}- \omega_{\rm N}) \cdot t).$$ | + | + \frac{A_{\rm N}}{2} \cdot {\cos} ( (\omega_{\rm T}- \omega_{\rm N}) \cdot t).\end{align*}$$ |
Der erste Term beschreibt den Träger, der zweite Term das sogenannte obere Seitenband (OSB) und der letzte Term das untere Seitenband (USB). | Der erste Term beschreibt den Träger, der zweite Term das sogenannte obere Seitenband (OSB) und der letzte Term das untere Seitenband (USB). | ||
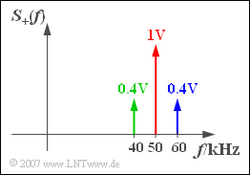
| − | Die Skizze zeigt das Spektrum | + | Die Skizze zeigt das Spektrum $S_+(f)$ des dazugehörigen analytischen Signals für $f_T = 50$ kHz. Man erkennt den Träger (rot), das obere Seitenband (blau) und das untere Seitenband (grün). |
| − | In der Teilaufgabe | + | In der Teilaufgabe 5) ist nach dem Betrag von $s_+(t)$ gefragt. Hierunter versteht man die Länge des resultierenden Zeigers. |
Hinweis: Diese Aufgabe bezieht sich auf die theoretischen Grundlagen von Kapitel 4.2. | Hinweis: Diese Aufgabe bezieht sich auf die theoretischen Grundlagen von Kapitel 4.2. | ||
Sie können Ihre Lösung mit dem folgenden Interaktionsmodul überprüfen: | Sie können Ihre Lösung mit dem folgenden Interaktionsmodul überprüfen: | ||
Zeigerdiagramm – Darstellung des analytischen Signals | Zeigerdiagramm – Darstellung des analytischen Signals | ||
| + | |||
| + | |||
===Fragebogen=== | ===Fragebogen=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Wie lautet das analytische Signal | + | {Wie lautet das analytische Signal $s_+(t)$. Wie groß ist dieses zur Zeit $t$ = 0? |
|type="{}"} | |type="{}"} | ||
$\text{Re}[s_+(t=0)] =$ { 1.8 } V | $\text{Re}[s_+(t=0)] =$ { 1.8 } V | ||
| Line 35: | Line 37: | ||
| − | {Welchen Wert besitzt das analytische Signal zur Zeit t = 5 μs? | + | {Welchen Wert besitzt das analytische Signal zur Zeit $t$ = 5 μs? |
|type="{}"} | |type="{}"} | ||
$\text{Re}[s_+(t=5 \mu \text{s})] =$ { 0 } V | $\text{Re}[s_+(t=5 \mu \text{s})] =$ { 0 } V | ||
$\text{Im}[s_+(t=5 \mu \text{s})] =$ { 1.761 3% } V | $\text{Im}[s_+(t=5 \mu \text{s})] =$ { 1.761 3% } V | ||
| − | {Welchen Wert besitzt | + | {Welchen Wert besitzt $s_+(t)$ zum Zeitpunkt $t$ = 20 μs? |
|type="{}"} | |type="{}"} | ||
$\text{Re}[s_+(t=20 \mu \text{s})] =$ { 1.237 3% } V | $\text{Re}[s_+(t=20 \mu \text{s})] =$ { 1.237 3% } V | ||
$\text{Im}[s_+(t=20 \mu \text{s})] =$ { 0 } V | $\text{Im}[s_+(t=20 \mu \text{s})] =$ { 0 } V | ||
| − | {Was ist die kleinstmögliche Zeigerlänge? Zu welchem Zeitpunkt | + | {Was ist die kleinstmögliche Zeigerlänge? Zu welchem Zeitpunkt t_{\text{min}} tritt dieser Wert zum ersten Mal auf? |
|type="{}"} | |type="{}"} | ||
$|s_+(t)|_{\text{min}} =$ {0.2 3%} V | $|s_+(t)|_{\text{min}} =$ {0.2 3%} V | ||
| Line 52: | Line 54: | ||
</quiz> | </quiz> | ||
| + | |||
===Musterlösung=== | ===Musterlösung=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1.''' | + | '''1.''' Durch Fourierrücktransformation von $S_+(f)$ unter Berücksichtigung des Verschiebungssatzes gilt: |
$$s_{+}(t) = {\rm 1 \hspace{0.05cm} V} \cdot {\rm e}^{{\rm | $$s_{+}(t) = {\rm 1 \hspace{0.05cm} V} \cdot {\rm e}^{{\rm | ||
| Line 64: | Line 67: | ||
40}\hspace{0.05cm} t }.$$ | 40}\hspace{0.05cm} t }.$$ | ||
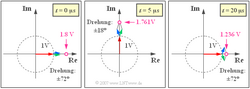
| − | Der Ausdruck beschreibt die Summe dreier Zeiger, die mit unterschiedlichen Winkelgeschwindigkeiten drehen. In obiger Gleichung bedeutet z. B. | + | Der Ausdruck beschreibt die Summe dreier Zeiger, die mit unterschiedlichen Winkelgeschwindigkeiten drehen. In obiger Gleichung bedeutet z. B. $\omega_{60} = 2\pi (f_T + f_N) = 2\pi \cdot 60$ kHz. Zum Zeitpunkt $t$ = 0 zeigen alle drei Zeiger in Richtung der reellen Achse (siehe linke Grafik), und man erhält den rein reellen Wert $s_+(t = 0) =$ 1.8 V. |
[[File:P_ID728__Sig_A_4_4_ML.png|250px|right|Analytische Signale (ML zu Aufgabe A4.4)]] | [[File:P_ID728__Sig_A_4_4_ML.png|250px|right|Analytische Signale (ML zu Aufgabe A4.4)]] | ||
| − | + | '''2.''' Die erste Aussage ist richtig und ergibt sich aus der Hilbert-Transformation. Dagegen stimmen die nächsten beiden Aussagen nicht: $s_+(t)$ ist stets eine komplexe Zeitfunktion mit Ausnahme des Grenzfalls $s(t)$ = 0. Jede komplexe Funktion hat jedoch zu einigen Zeitpunkten auch rein reelle Werte. | |
| − | Der Zeigerverbund dreht immer in mathematisch positiver Richtung. Überschreitet der Summenvektor die reelle Achse, so verschwindet zu diesem Zeitpunkt der Imaginärteil und | + | Der Zeigerverbund dreht immer in mathematisch positiver Richtung. Überschreitet der Summenvektor die reelle Achse, so verschwindet zu diesem Zeitpunkt der Imaginärteil und $s_+(t)$ ist rein reell. |
| − | + | ||
| + | '''3.''' Die Periodendauer des Trägersignals beträgt $T_0 = 1/f_T =$ 20 μs. Nach $t$ = 5 μs hat sich der Träger somit um 90° gedreht (siehe mittlere Grafik). Der blaue Zeiger (OSB) dreht um 20% schneller, der grüne (USB) um 20% langsamer als der rote Drehzeiger (Trägersignal): | ||
| − | $$s_{+}({\rm 5 \hspace{0.05cm} \mu s}) & = | + | $$\begin{align*}s_{+}({\rm 5 \hspace{0.05cm} \mu s}) & = {\rm 1 |
\hspace{0.05cm} V} \cdot {\rm e}^{{\rm j}\hspace{0.05cm} 2 \pi | \hspace{0.05cm} V} \cdot {\rm e}^{{\rm j}\hspace{0.05cm} 2 \pi | ||
\hspace{0.03cm} \cdot \hspace{0.08cm}50 \hspace{0.03cm} \cdot | \hspace{0.03cm} \cdot \hspace{0.08cm}50 \hspace{0.03cm} \cdot | ||
| Line 79: | Line 83: | ||
}+ {\rm 0.4 \hspace{0.05cm} V} \cdot {\rm e}^{{\rm | }+ {\rm 0.4 \hspace{0.05cm} V} \cdot {\rm e}^{{\rm | ||
j}\hspace{0.05cm} 2 \pi \hspace{0.03cm} \cdot \hspace{0.08cm}40 | j}\hspace{0.05cm} 2 \pi \hspace{0.03cm} \cdot \hspace{0.08cm}40 | ||
| − | \hspace{0.03cm} \cdot \hspace{0.08cm}0.005 } =\\ & = | + | \hspace{0.03cm} \cdot \hspace{0.08cm}0.005 } =\\ & = {\rm 1 |
\hspace{0.05cm} V} \cdot {\rm e}^{{\rm j}\hspace{0.05cm} 90^\circ | \hspace{0.05cm} V} \cdot {\rm e}^{{\rm j}\hspace{0.05cm} 90^\circ | ||
}+ {\rm 0.4 \hspace{0.05cm} V} \cdot {\rm e}^{{\rm | }+ {\rm 0.4 \hspace{0.05cm} V} \cdot {\rm e}^{{\rm | ||
j}\hspace{0.05cm} 108^\circ }+{\rm 0.4 \hspace{0.05cm} V} \cdot | j}\hspace{0.05cm} 108^\circ }+{\rm 0.4 \hspace{0.05cm} V} \cdot | ||
| − | {\rm e}^{{\rm j}\hspace{0.05cm} 72^\circ }.$$ | + | {\rm e}^{{\rm j}\hspace{0.05cm} 72^\circ }.\end{align*}$$ |
| − | Somit sind die in 5 μs zurückgelegten Winkel von OSB und USB 108° bzw. 72°. Da sich zu diesem Zeitpunkt die Realteile von OSB und USB kompensieren, ist | + | Somit sind die in 5 μs zurückgelegten Winkel von OSB und USB 108° bzw. 72°. Da sich zu diesem Zeitpunkt die Realteile von OSB und USB kompensieren, ist $s_+(t =$ 5 μs) rein imaginär und man erhält: |
$${\rm Im}\left[s_{+}(t = {\rm 5 \hspace{0.05cm} \mu s})\right] = | $${\rm Im}\left[s_{+}(t = {\rm 5 \hspace{0.05cm} \mu s})\right] = | ||
| Line 91: | Line 95: | ||
V}\cdot \cos (18^\circ ) \hspace{0.15 cm}\underline{= {\rm 1.761 \hspace{0.05cm} V}}.$$ | V}\cdot \cos (18^\circ ) \hspace{0.15 cm}\underline{= {\rm 1.761 \hspace{0.05cm} V}}.$$ | ||
| − | + | '''4.''' Nach einer Umdrehung des roten Trägers, also zum Zeitpunkt $t$ = $T_0$ = 20 μs, hat der blaue Zeiger bereits 72° mehr zurückgelegt; der grüne Zeiger 72° weniger. Die Summe der drei Zeiger ist wieder rein reell und ergibt (siehe rechte Grafik): | |
$${\rm Re}\left[s_{+}({\rm 20 \hspace{0.05cm} \mu s})\right] = | $${\rm Re}\left[s_{+}({\rm 20 \hspace{0.05cm} \mu s})\right] = | ||
| Line 97: | Line 101: | ||
V}\cdot \cos (72^\circ ) \hspace{0.15 cm}\underline{= {\rm 1.237 \hspace{0.05cm} V}}.$$ | V}\cdot \cos (72^\circ ) \hspace{0.15 cm}\underline{= {\rm 1.237 \hspace{0.05cm} V}}.$$ | ||
| − | + | '''5.''' Der Betrag ist minimal, wenn die Zeiger der beiden Seitenbänder gegenüber dem Träger um 180° versetzt sind. Daraus folgt: | |
$$|s_{+}(t)|_{\rm min} = {\rm 1 \hspace{0.05cm} V} - 2 \cdot {\rm | $$|s_{+}(t)|_{\rm min} = {\rm 1 \hspace{0.05cm} V} - 2 \cdot {\rm | ||
0.4 \hspace{0.05cm} V} \hspace{0.15 cm}\underline{= {\rm 0.2 \hspace{0.05cm} V}}.$$ | 0.4 \hspace{0.05cm} V} \hspace{0.15 cm}\underline{= {\rm 0.2 \hspace{0.05cm} V}}.$$ | ||
| − | Innerhalb einer Periode | + | Innerhalb einer Periode $T_0$ des Trägers tritt gegenüber den Zeigern der beiden Seitenbändern ein Phasenversatz von ±72° auf. Daraus folgt: $t_{\text{min}}$ = 2.5 $\cdot T_0$ = 50 μs. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
__NOEDITSECTION__ | __NOEDITSECTION__ | ||
[[Category:Aufgaben zu Signaldarstellung|^4. Bandpassartige Signale^]] | [[Category:Aufgaben zu Signaldarstellung|^4. Bandpassartige Signale^]] | ||
Revision as of 18:41, 19 April 2016
Wir gehen von einem cosinusförmigen Quellensignal $q(t)$ mit der Amplitude $A_N$ = 0.8 V und der Frequenz $f_N$ = 10 kHz aus. Die Frequenzumsetzung erfolgt mittels Zweiseitenband–Amplitudenmodulation mit Träger, abgekürzt ZSB–AM. Das modulierte Signal $s(t)$ lautet mit dem (normierten) Träger $z(t) = \text{cos}(\omega T \dot t)$ und dem Gleichanteil $q_0$ = 1 V:
$$\begin{align*} s(t) & = \left(q_0 + q(t)\right) \cdot z(t)= \left({\rm 1 \hspace{0.05cm} V} + {\rm 0.8 \hspace{0.05cm}V}\cdot {\cos} ( \omega_{\rm N}\cdot t)\right) \cdot {\cos} ( \omega_{\rm T}\cdot t) = \\ & = q_0 \cdot {\cos} ( \omega_{\rm T}\cdot t) + \frac{A_{\rm N}}{2} \cdot {\cos} ( (\omega_{\rm T}+ \omega_{\rm N}) \cdot t) + \frac{A_{\rm N}}{2} \cdot {\cos} ( (\omega_{\rm T}- \omega_{\rm N}) \cdot t).\end{align*}$$
Der erste Term beschreibt den Träger, der zweite Term das sogenannte obere Seitenband (OSB) und der letzte Term das untere Seitenband (USB). Die Skizze zeigt das Spektrum $S_+(f)$ des dazugehörigen analytischen Signals für $f_T = 50$ kHz. Man erkennt den Träger (rot), das obere Seitenband (blau) und das untere Seitenband (grün). In der Teilaufgabe 5) ist nach dem Betrag von $s_+(t)$ gefragt. Hierunter versteht man die Länge des resultierenden Zeigers. Hinweis: Diese Aufgabe bezieht sich auf die theoretischen Grundlagen von Kapitel 4.2. Sie können Ihre Lösung mit dem folgenden Interaktionsmodul überprüfen: Zeigerdiagramm – Darstellung des analytischen Signals
Fragebogen
Musterlösung
$$s_{+}(t) = {\rm 1 \hspace{0.05cm} V} \cdot {\rm e}^{{\rm j}\hspace{0.05cm} \omega_{\rm 50}\hspace{0.05cm} t } + {\rm 0.4 \hspace{0.05cm} V} \cdot {\rm e}^{{\rm j}\hspace{0.05cm} \omega_{\rm 60} \hspace{0.05cm} t }+ {\rm 0.4 \hspace{0.05cm} V} \cdot {\rm e}^{{\rm j}\hspace{0.05cm} \omega_{\rm 40}\hspace{0.05cm} t }.$$
Der Ausdruck beschreibt die Summe dreier Zeiger, die mit unterschiedlichen Winkelgeschwindigkeiten drehen. In obiger Gleichung bedeutet z. B. $\omega_{60} = 2\pi (f_T + f_N) = 2\pi \cdot 60$ kHz. Zum Zeitpunkt $t$ = 0 zeigen alle drei Zeiger in Richtung der reellen Achse (siehe linke Grafik), und man erhält den rein reellen Wert $s_+(t = 0) =$ 1.8 V.
2. Die erste Aussage ist richtig und ergibt sich aus der Hilbert-Transformation. Dagegen stimmen die nächsten beiden Aussagen nicht: $s_+(t)$ ist stets eine komplexe Zeitfunktion mit Ausnahme des Grenzfalls $s(t)$ = 0. Jede komplexe Funktion hat jedoch zu einigen Zeitpunkten auch rein reelle Werte. Der Zeigerverbund dreht immer in mathematisch positiver Richtung. Überschreitet der Summenvektor die reelle Achse, so verschwindet zu diesem Zeitpunkt der Imaginärteil und $s_+(t)$ ist rein reell.
3. Die Periodendauer des Trägersignals beträgt $T_0 = 1/f_T =$ 20 μs. Nach $t$ = 5 μs hat sich der Träger somit um 90° gedreht (siehe mittlere Grafik). Der blaue Zeiger (OSB) dreht um 20% schneller, der grüne (USB) um 20% langsamer als der rote Drehzeiger (Trägersignal):
$$\begin{align*}s_{+}({\rm 5 \hspace{0.05cm} \mu s}) & = {\rm 1 \hspace{0.05cm} V} \cdot {\rm e}^{{\rm j}\hspace{0.05cm} 2 \pi \hspace{0.03cm} \cdot \hspace{0.08cm}50 \hspace{0.03cm} \cdot \hspace{0.08cm}0.005 } + {\rm 0.4 \hspace{0.05cm} V} \cdot {\rm e}^{{\rm j}\hspace{0.05cm} 2 \pi \hspace{0.03cm} \cdot \hspace{0.08cm}60 \hspace{0.03cm} \cdot \hspace{0.08cm}0.005 }+ {\rm 0.4 \hspace{0.05cm} V} \cdot {\rm e}^{{\rm j}\hspace{0.05cm} 2 \pi \hspace{0.03cm} \cdot \hspace{0.08cm}40 \hspace{0.03cm} \cdot \hspace{0.08cm}0.005 } =\\ & = {\rm 1 \hspace{0.05cm} V} \cdot {\rm e}^{{\rm j}\hspace{0.05cm} 90^\circ }+ {\rm 0.4 \hspace{0.05cm} V} \cdot {\rm e}^{{\rm j}\hspace{0.05cm} 108^\circ }+{\rm 0.4 \hspace{0.05cm} V} \cdot {\rm e}^{{\rm j}\hspace{0.05cm} 72^\circ }.\end{align*}$$
Somit sind die in 5 μs zurückgelegten Winkel von OSB und USB 108° bzw. 72°. Da sich zu diesem Zeitpunkt die Realteile von OSB und USB kompensieren, ist $s_+(t =$ 5 μs) rein imaginär und man erhält:
$${\rm Im}\left[s_{+}(t = {\rm 5 \hspace{0.05cm} \mu s})\right] = {\rm 1 \hspace{0.05cm} V} + 2 \cdot {\rm 0.4 \hspace{0.05cm} V}\cdot \cos (18^\circ ) \hspace{0.15 cm}\underline{= {\rm 1.761 \hspace{0.05cm} V}}.$$
4. Nach einer Umdrehung des roten Trägers, also zum Zeitpunkt $t$ = $T_0$ = 20 μs, hat der blaue Zeiger bereits 72° mehr zurückgelegt; der grüne Zeiger 72° weniger. Die Summe der drei Zeiger ist wieder rein reell und ergibt (siehe rechte Grafik):
$${\rm Re}\left[s_{+}({\rm 20 \hspace{0.05cm} \mu s})\right] = {\rm 1 \hspace{0.05cm} V} + 2 \cdot {\rm 0.4 \hspace{0.05cm} V}\cdot \cos (72^\circ ) \hspace{0.15 cm}\underline{= {\rm 1.237 \hspace{0.05cm} V}}.$$
5. Der Betrag ist minimal, wenn die Zeiger der beiden Seitenbänder gegenüber dem Träger um 180° versetzt sind. Daraus folgt:
$$|s_{+}(t)|_{\rm min} = {\rm 1 \hspace{0.05cm} V} - 2 \cdot {\rm 0.4 \hspace{0.05cm} V} \hspace{0.15 cm}\underline{= {\rm 0.2 \hspace{0.05cm} V}}.$$
Innerhalb einer Periode $T_0$ des Trägers tritt gegenüber den Zeigern der beiden Seitenbändern ein Phasenversatz von ±72° auf. Daraus folgt: $t_{\text{min}}$ = 2.5 $\cdot T_0$ = 50 μs.