Aufgaben:Exercise 3.10: Rayleigh Fading

• Return to book

Rayleigh PDF

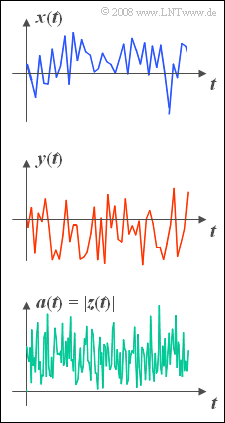
One often describes a bandpass transmission system in the so-called equivalent lowpass domain.  This representation leads according to the chapter "Bandpass-like signals" in the book  Signal Representation  to a complex signal:

$$z(t)=x(t)+ {\rm j} \cdot y(t).$$

The real part  $x(t)$  denotes the  inphase component  and the imaginary part  $y(t)$  the  quadrature component.

In a mobile radio system where there is no line of sight between the mobile user and the base station, the radio signal thus reaches the receiver exclusively by indirect means (refraction, scattering, reflection, etc.);

In this case, the following model is applicable:

• The real part $x(t)$  and also the imaginary part $y(t)$  are both distributed and zero mean.
• $x(t)$  and  $y(t)$  each have the same rms  $\sigma$  and are independent of each other.
• Internal binding of the signals  $x(t)$  and  $y(t)$  due to the Doppler effect shall not be considered here.

The complex signal  $z(t)$  can also be represented by magnitude and phase:

$$ z(t)= a(t)\cdot {\rm e}^{\rm j \phi(t)}.$$

• Because of symmetry with respect to  $x(t)$  and  $y(t)$  the phase  $\phi(t)$  is uniformly distributed.
• In contrast, the magnitude  $a(t) = |z(t)|$  is Rayleigh distributed, which has led to the naming "Rayleigh fading".
• As a further quantity we define the instantaneous power

$$ p(t)=x^{\rm 2}(t)+y^{\rm 2}( t)=a^{\rm 2}(t).$$

The random variable  $p$  is  (one-sided) exponentially distributed.  Its PDF is for  $p>0$:

$$f_p(p)=\frac{1}{2\sigma^{\rm 2}}\cdot {\rm e}^{ -p/(\sigma^{\rm 2})}.$$

For all negative $p$–values, of course  $f_p(p)= 0$ holds, since  $p$  denotes a power.

Hints:

• This exercise belongs to the chapter  Further Distributions.
• In particular, reference is made to the page  Rayleigh PDF.
• The rms of the two Gaussian random variables  $x$  and  $y$  are each  $\sigma = 1$.
• All variables are therefore to be understood as normalized.

Questions

1

Which of the following statements are always true?

	Small instantaneous powers are more likely than large ones.
	The phase  $\phi(t) = \pi/2$  also means "imaginary part $y(t) = 0$".
	The phase  $\phi(t) = -\pi/2$  also means "real part $x(t) = 0$".

2

With what probability is the (normalized) instantaneous power  $p(t)$  greater than  $4$?

${\rm Pr}(p(t) > 4) \ = \ $ $\ \%$

3

What is the probability that the magnitude  $a(t)$  is greater than  $2$  ?

${\rm Pr}(a(t) > 2) \ = \ $ $\ \%$

4

Calculate, starting from  $f_p(p)$  the PDF of the random variable  $a$.  What PDF value results for  $a=1$?

$f_a(a = 1)\ = \ $

Solution

Solution

(1)  Correct are the first and the third proposed solutions:

• The first statement is true because of the exponential distribution for  $p(t)$ .
• A phase angle  $\phi(t) = \pm \pi/2 \ (\pm 90^\circ)$  means that the real part  $x(t) = 0$ .
• For positive imaginary part ⇒  $y(t) > 0$  the phase angle  $\phi(t) = +90^\circ$, for negative imaginary part the phase angle  $\phi(t) = -90^\circ$.

(2)  With  $\sigma = 1$  holds for the PDF of the instantaneous power:

$$f_p(p)= {\rm 1}/{\rm 2}\cdot{\rm e}^{-p/\rm 2}.$$

• The probability we are looking for is thus:

$${\rm Pr}(p(t) > 4) = \int_{\rm 4}^{\infty}{1}/{2}\cdot{\rm e}^{-p/\rm 2}\,{\rm d} p={\rm e}^{\rm -2} \rm \hspace{0.15cm}\underline{=13.5\%}.$$

(3)  Since  $p(t) =a^2(t)$  holds and moreover  $a(t) < 0$  is not possible, the event  $a(t) > 2$  is identical to the event  $p(t) > 4$:

• It results in the same probability  ${\rm Pr}(a(t) > 2) \hspace{0.15cm}\underline{=13.5\%}$  as calculated in  (2) .

(4)  In general:

$$f_a(a)=\frac{f_p(p)}{|g'(p)|}\Bigg |_{\, p=h(a)}.$$

• The transformation characteristic is:

$$g\hspace{0.05cm}'(p)=\frac{ {\rm d} a}{ {\rm d} p}=\frac{1}{2 \cdot \sqrt{p}}.$$

• This is always positive.  It follows for the Rayleigh PDF:

$$f_a(a)=\sqrt {p}\cdot {\rm e}^{ -p/\rm 2}\Big|_{ p=a^{\rm 2}}= a\cdot {\rm e}^{\, -a^{\rm 2}/\rm 2}.$$

• For  $a = 1$  this gives the value  $f_a(a = 1)= {\rm e}^{-0.5}\hspace{0.15cm}\underline{=0.607} $.