Aufgaben:Exercise 5.8: Equalization in Matrix Vector Notation

• Return to book

Block diagram of OFDM transmission KORREKTUR: cyclic prefix ...

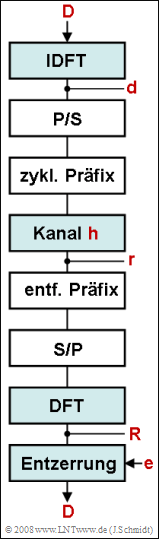
We consider the blocks of an OFDM system shown in the diagram,  assuming a system with  $N = 4$  carriers and a channel with  $L = 2$  echoes.

• Only a single frame is considered and for the transmission vector  (in the time domain),  we apply:

$${\rm\bf{d}} = (d_0, \ d_1,\ d_2,\ d_3 ) = (+1, -1, +1, -1 ).$$

• Let the channel impulse response be described by

$${\rm\bf{h}} = (h_0, \ h_1,\ h_2 ) = (0, \ 0.6, \ 0.4 ).$$

• To represent the cyclic prefix in this task,  instead of the extended transmission vector with the associated transmission matrix  ${\rm\bf{H}}_{\rm ext}$,  we use the cyclic transmission matrix

$${\rm\bf{H}}_{\rm{C}} = \left( {\begin{array}{*{20}c} {h_0 } & {h_1 } & {h_2 } & {} \\ {} & {h_0 } & {h_1 } & {h_2 } \\ \hline {h_2 } & {} & {h_0 } & {h_1 } \\ {h_1 } & {h_2 } & {} & {h_0 } \\ \end{array}} \right).$$

• For the spectral coefficients at the receiver,  according to the Discrete Fourier Transform  $\rm (DFT)$:

$${\rm\bf{R}} = {\rm\bf{D}} \cdot \left( {\begin{array}{*{20}c} {H_0 } & {} & {} & {} \\ {} & {H_1 } & {} & {} \\ {} & {} & {H_2 } & {} \\ {} & {} & {} & {H_3 } \\ \end{array}} \right) ,$$

where the diagonal elements are to be calculated as follows:

$$H_\mu = \sum\limits_{l = 0}^2 {h_l \cdot {\rm{e}}^{ - {\rm{j\hspace{0.04cm}\cdot \hspace{0.04cm}2\pi }} \hspace{0.04cm}\cdot \hspace{0.04cm} l \hspace{0.04cm}\cdot \hspace{0.04cm} {\mu }/{4}} } .$$

• The equalization at the receiver is done by multiplication in the frequency domain by the coefficients  $ e_\mu = {1}/{H_\mu }.$

Notes:

• The exercise belongs to the chapter  Implementation of OFDM Systems.
• Reference is also made to the chapter  Discrete Fourier Transform  in the book  "Signal Representation".

• For the Discrete Fourier Transform (DFT) in matrix-vector notation holds:

$${\rm\bf{F}} = \left( {\begin{array}{*{20}c} 1 & 1 & \cdots & 1 \\ 1 & {} & {} & {} \\ \vdots & {} & {{\rm{e}}^{ - {\rm{j2\pi }}{\kern 1pt} \nu {\kern 1pt} \mu /N} } & {} \\ 1 & {} & {} & {} \\ \end{array}} \right), \qquad {\rm{DFT\; with}} \; {1}/{N} \cdot {\rm\bf{F}}; \qquad {\rm{IDFT \; with}} \; {\rm\bf{F}}^*.$$

Questions

1

Calculate the discrete reception values  $r = (r_0, r_1, r_2, r_3)$  in the time domain.  Enter  $r_0$  and  $r_1$  as a check.

${\rm Re}\big[r_0\big] \ = \ $

${\rm Im}\big[r_0\big] \ = \ $

${\rm Re}\big[r_1\big] \ = \ $

${\rm Im}\big[r_1\big] \ = \ $

2

What are the discrete spectral domain coefficients  ${\rm\bf{D}}= (D_0, D_1, D_2, D_3)$  at the transmitter?  Enter  $D_2$  and  $D_3$  as a check.

${\rm Re}\big[D_2\big] \ = \ $

${\rm Im}\big[D_2\big] \ = \ $

${\rm Re}\big[D_3\big] \ = \ $

${\rm Im}\big[D_3\big] \ = \ $

3

Calculate the discrete spectral coefficients  ${\rm\bf{R}}= (R_0, R_1, R_2, R_3)$  according to the channel.  Enter  $R_2$  and  $R_3$  as a check.

${\rm Re}\big[R_2\big] \ = \ $

${\rm Im}\big[R_2\big] \ = \ $

${\rm Re}\big[R_3\big] \ = \ $

${\rm Im}\big[R_3\big] \ = \ $

4

Determine the discrete equalizer coefficients  ${\rm\bf{e}}= (e_0, e_1, e_2, e_3)$.

${\rm Re}\big[e_0\big] \ = \ $

${\rm Im}\big[e_0\big] \ = \ $

${\rm Re}\big[e_1\big] \ = \ $

${\rm Im}\big[e_1\big] \ = \ $

${\rm Re}\big[e_2\big] \ = \ $

${\rm Im}\big[e_2\big] \ = \ $

${\rm Re}\big[e_3\big] \ = \ $

${\rm Im}\big[e_3\big] \ = \ $

5

What is the name of the equalization approach used?

	As "Zero Forcing" approach,
	as "Matched Filter" approach,
	as "Minimum Mean Square Error  $\rm (MMSE)$”approach.

Solution

Solution

(1)  The discrete time domain values at the receiver are calculated using the cyclic transmission matrix  ${\rm\bf{H}}_{\rm{C}} $  as follows:

$${\rm\bf{r}} = {\rm\bf{d}} \cdot {\rm\bf{H}}_{\rm{C}} = \left( {+1 ,-1 ,+1 ,-1 } \right) \cdot \left( {\begin{array}{*{20}c} {0 } & {0.6 } & {0.4 } & {} \\ {} & {0 } & {0.6 } & {0.4 } \\ \hline {0.4 } & {} & {0 } & {0.6 } \\ {0.6 } & {0.4 } & {} & {0 } \\ \end{array}} \right)$$

$$\Rightarrow \hspace{0.3cm}{\rm\bf{r}} = \left( {r_0 ,r_1 ,r_2 ,r_3 } \right) = \left( {-0.2, +0.2,-0.2, +0.2} \right) \hspace{0.3cm} \Rightarrow \hspace{0.3cm}{\rm Re}[r_0]\hspace{0.15cm} \underline{=-0.2},\hspace{0.2cm} {\rm Im}[r_0]\hspace{0.15cm} \underline{=0}, \hspace{0.2cm}{\rm Re}[r_1]\hspace{0.15cm} \underline{=+0.2},\hspace{0.2cm} {\rm Im}[r_1]\hspace{0.15cm} \underline{=0}. $$

(2)  The spectral coefficients  ${\rm\bf{D}}$  result directly from the Discrete Fourier Transform  $\rm (DFT)$  of the time domain coefficients  ${\rm\bf{d}}= (+1, -1, +1, -1)$.

• This time domain sequence corresponds to a discrete cosine function with twice the fundamental frequency  $(2 \cdot f_0)$  and amplitude  $1$.  It follows:

$${\rm\bf{D}} = \left( {D_0 ,D_1 ,D_2 ,D_3 } \right) =\left( {0, 0,1, 0} \right)\hspace{0.3cm} \Rightarrow \hspace{0.3cm}{\rm Re}[d_2]\hspace{0.15cm} \underline{=1},\hspace{0.2cm} {\rm Im}[d_2]\hspace{0.15cm} \underline{=0}, \hspace{0.2cm}{\rm Re}[d_3]\hspace{0.15cm} \underline{=0},\hspace{0.2cm} {\rm Im}[d_3]\hspace{0.15cm} \underline{=0}.$$

(3)  The vector  ${\rm\bf{R}}$  of spectral coefficients after the channel could be calculated by DFT of the vector   ${\rm\bf{r}}$,  analogous to subtask  (2). 

• An alternative solution path is:

$${\rm\bf{R}} = {\rm\bf{D}} \cdot \left( {\begin{array}{*{20}c} {H_0 } & {} & {} & {} \\ {} & {H_1 } & {} & {} \\ {} & {} & {H_2 } & {} \\ {} & {} & {} & {H_3 } \\ \end{array}} \right) .$$

• For the diagonal elements one obtains:

$$H_\mu = \sum\limits_{l = 0}^2 {h_l \cdot {\rm{e}}^{ - {\rm{j\hspace{0.04cm}\cdot \hspace{0.04cm}2\pi }} \hspace{0.04cm}\cdot \hspace{0.04cm} l \hspace{0.04cm}\cdot \hspace{0.04cm}{\mu }/{4}} } \hspace{0.3cm} \Rightarrow \hspace{0.3cm} H_0 = 1,\hspace{0.1cm}H_1 = -0.4 - {\rm{j}} \cdot 0.6,\hspace{0.1cm}H_2 = -0.2,\hspace{0.1cm}H_3 = -0.4 + {\rm{j}} \cdot 0.6 $$

$$\Rightarrow \hspace{0.3cm}{\rm\bf{R}} = \left( {R_0 ,R_1 ,R_2 ,R_3 } \right)= \left( \hspace{0.15cm}0,\hspace{0.15cm}0,\hspace{0.15cm}-0.2, \hspace{0.15cm}0 \right) \hspace{0.3cm} \Rightarrow \hspace{0.3cm}{\rm Re}[r_2]\hspace{0.15cm} \underline{=-0.2},\hspace{0.2cm} {\rm Im}[r_2]\hspace{0.15cm} \underline{=0}, \hspace{0.2cm}{\rm Re}[r_3]\hspace{0.15cm} \underline{=0},\hspace{0.2cm} {\rm Im}[r_3]\hspace{0.15cm} \underline{=0}.$$

(4)  The equalizer coefficients result in  $e_\mu = 1/H_\mu$.

• With the result from subtask  (3),  the coefficients  $e_0 = 1$,  $e_2 = -5$ are real:

$${\rm Re}[e_0]\hspace{0.15cm} \underline{=1},\hspace{0.2cm} {\rm Im}[e_0]\hspace{0.15cm} \underline{=0}, \hspace{0.2cm}{\rm Re}[e_2]\hspace{0.15cm} \underline{=-5},\hspace{0.2cm} {\rm Im}[e_2]\hspace{0.15cm} \underline{=0}.$$

• For the other two coefficients:

$$e_1 = \frac {1}{-0.4 - {\rm{j}} \cdot 0.6} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} {\rm{Re}}[e_1] = \frac {-0.4}{0.4^2 + 0.6^2}\hspace{0.15cm} \underline{ \approx -0.77},\hspace{0.3cm} {\rm{Im}}[e_1] = \frac {0.6}{0.4^2 + 0.6^2} \hspace{0.15cm} \underline{\approx +1.15},$$

$$e_3 = \frac {1}{-0.4 + {\rm{j}} \cdot 0.6} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} {\rm{Re}}[e_3] = \frac {-0.4}{0.4^2 + 0.6^2}\hspace{0.15cm} \underline{ \approx -0.77},\hspace{0.3cm} {\rm{Im}}[e_3] = \frac {-0.6}{0.4^2 + 0.6^2} \hspace{0.15cm} \underline{\approx -1.15}.$$

(5)  The equalization calculated in  (4)  follows the  "zero forcing"  approach   ⇒   solution 1.