Aufgaben:Exercise 4.1: Triangular (x, y) Area

• Return to book

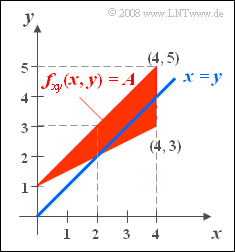
Triangular two-dimensional area

A two-dimensional random variable is defined by the adjacent sketch:

• For  $(x, \ y)$  only values within the triangular-shaped region defined by the three vertices  $(0,\ 1)$,$  $(4,\ 3)$,$  and  $(4,\ 5)$  can occur.
• Within the triangle,  all the random variables  $(x,\ y)$  are equally probable.
• For the 2D–PDF,  in this domain:

$$f_{xy}(x,y) = A .$$

In addition,  the straight line  $x = y$  ⇒   "angle bisector"  is drawn in the graphic  ⇒  see subtask  (2).

Hint:

• The exercise belongs to the chapter  Two-Dimensional Random Variables.

Questions

1

Determine the PDF constant using geometric considerations.

$A \ = \ $

2

Calculate the probability that  $x$  is greater than  $y$.

${\rm Pr}(x > y) \ = \ $

3

Determine the marginal PDF  $f_x(x)$.  Calculate the probability that  $x$  is greater than or equal to  $2$.
Check the value with the 2D–PDF.

${\rm Pr}(x ≥ 2)\ = \ $

4

Determine the marginal PDF  $f_y(y)$.  Calculate the probability that  $y$  is greater than or equal to  $3$.
Check the value with the 2D–PDF.

${\rm Pr}(y ≥ 3)\ = \ $

5

What is the probability that the random variable  $x$  is greater than or equal to  $2$  and at the same time the random variable  $y$  is greater than or equal to $3$?

${\rm Pr}\big[(x ≥ 2) ∩ (y ≥ 3)\big]\ = \ $

6

What is the probability that  $x$  is greater than or equal to  $2$  given  $y \ge 3$?

${\rm Pr}\big[x ≥ 2\hspace{0.05cm} | \hspace{0.05cm} y ≥ 3\big]\ = \ $

7

What is the probability that  $y \ge 3$  given that  $x \ge 2$  holds?

${\rm Pr}\big[y ≥ 3\hspace{0.05cm} | \hspace{0.05cm} x ≥ 2\big]\ = \ $

Solution

Solution

(1)  The volume under the two dimensional PDF is by definition equal to  $1$:

Triangular 2D PDF

$$\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}f_{xy}(x,y)\, {\rm d}x\, {\rm d}y=1.$$

• The triangle area is  $D = 0.5 \cdot 2 \cdot 4 = 4$.
• Since in this definition area the PDF is constantly equal to  $A$ , we get.

$$A= 1/D\hspace{0.15cm}\underline{= 0.25}.$$

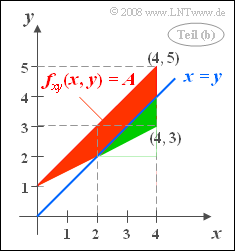
(2)  For the solution we start from the adjacent sketch.

• The area  $x>y$  lies to the right of the angle bisector  $x=y$  and is marked in green.

• This green triangular area is  $D_{\rm (2)} = 0.5 \cdot 1 \cdot 2 = 1 $, i.e. exactly one quarter of the total area  $D$  of the definition area.
• From this follows  ${\rm Pr}(x > y)\hspace{0.15cm}\underline{= 0.25}$.

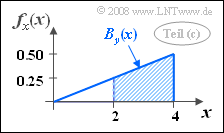
(3)  For the wanted marginal PDF holds in this case:

marginal PDF with respect to  $x$

$$f_x(x)=\int_{-\infty}^{+\infty}f_{xy}(x,y)\, {\rm d}y=A\cdot B_y (x).$$

• Here denotes  $B_y(x)$  the width of the area  $f_{xy} \ne 0$  in  $y$–direction at the considered  $x$–value.
• It holds:  $B_y(x) = x/2$.  With  $A = 0.25$  it follows  $f_{x}(x) = x/8$  for the range  $ 0 \le x \le 4$.

• The wanted probability corresponds to the shaded area in the accompanying sketch.  One obtains:

$$\rm Pr(\it x\ge \rm 2) = \rm 1-\rm Pr(\it x < \rm 2) = \rm 1-\frac{1}{2}\cdot2\cdot 0.25\hspace{0.15cm}\underline{ =0.75}. $$

• The same result is obtained using 2D PDF:  To the right of  $x = 2$  lies  $3/4$  of the total definition area.

marginal PDF with respect to  $y$

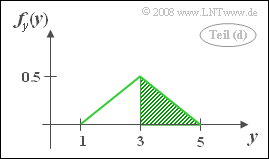
(4)  Analogous to the sample solution to the subtask  (3)  holds:

$$f_y(y)=\int_{-\infty}^{+\infty}f_{xy}(x,y)\, {\rm d}x=A\cdot B_x (y).$$

• The spread of PDF area in  $x$–direction is zero for  $y \le 1$  and  $y \ge 5$  respectively.
• The maximum is at  $y=3$  and gives  $B_x(y=3) = 2$.
• In between, the increase  and decrease of  $B_x(y)$  is linear, yielding a triangular-shaped PDF.
• The probability that  $y \is 3$  corresponds to the green shaded area in the adjacent sketch.
• Because of the symmetry, one obtains:

$${\rm Pr}(y ≥ 3)\hspace{0.15cm}\underline{ =0.5}. $$

The same result is obtained using 2D PDF:   Above the horizontal  $y= 3$  lies half of the total definition area.

On subtask (5)

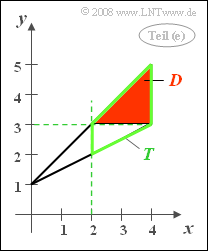
(5)  If  $y \ge 3$  is  $($red highlighted triangle  $D)$,  is always also true  $x \ge 2$  $($green outlined trapezoid  $T)$.

• This means:  In this example  $D$  is a subset of  $T$, and it holds:

$${\rm Pr}[(x ≥ 2) ∩ (y ≥ 3)] = {\rm Pr}(y ≥ 3) \hspace{0.15cm}\underline{= 0.50}.$$

(6)  According to the solution to the subtask  (5)  it follows from  $y \ge 3$  with certainty also  $x \ge 2$.

• So the conditional probability we are looking for is:

$${\rm Pr}[x ≥ 2\hspace{0.05cm} | \hspace{0.05cm} y ≥ 3]\hspace{0.15cm}\underline{= 1}.$$

(7)  This subtask can be solved using Bayes' theorem and the results from  (2)  and  (5)  :

$$\rm Pr(\it y \ge \rm 3\hspace{0.1cm}|\hspace{0.1cm} \it x \ge \rm 2) = \frac{ \rm Pr((\it x \ge \rm 2)\cap(\it y \ge \rm 3))} {\rm Pr(\it x \ge \rm 2)}=2/3\hspace{0.15cm}\underline{=0.667}.$$

• Or expressed differently:   The area  $D$  of the triangle with red background makes  $2/3$  of the area of the trapezoid with green border  $T$ .