Difference between revisions of "Aufgaben:Exercise 4.2: Triangle Area again"
| Line 4: | Line 4: | ||
[[File:P_ID226__Sto_A_4_2.png|right|frame|Triangular 2D area and the two marginal probability densities]] | [[File:P_ID226__Sto_A_4_2.png|right|frame|Triangular 2D area and the two marginal probability densities]] | ||
| − | We consider the same random variable $(x, \ y)$ as in | + | We consider the same random variable $(x, \ y)$ as in [[Aufgaben:Exercise_4.1:_Triangular_(x,_y)_Area|Exercise 4.1]]: |
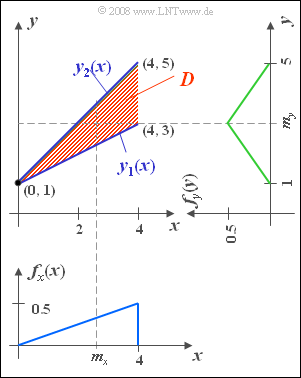
| − | *In a domain defined by vertices $(0,\ 1)$, $(4,\ 3)$, and $(4,\ 5)$ let the 2D–PDF $f_{xy} (x, y) = 0.25$. | + | *In a domain defined by vertices $(0,\ 1)$, $(4,\ 3)$, and $(4,\ 5)$ let the 2D–PDF $f_{xy} (x, y) = 0.25$. |
*There are no values outside this definition area $D$ marked in red in the graph. | *There are no values outside this definition area $D$ marked in red in the graph. | ||
| − | Furthermore, the two marginal probability densities with respect to the quantities $x$ and $y$ are drawn in the graph, which have already been determined in Exercise 4.1. | + | Furthermore, the two marginal probability densities with respect to the quantities $x$ and $y$ are drawn in the graph, which have already been determined in Exercise 4.1. |
| − | From this, the equations of chapter [[Theory_of_Stochastic_Signals/Expected_Values_and_Moments|Expected Values and Moments]] can be used to determine the characteristics of the two random variables: | + | From this, the equations of chapter [[Theory_of_Stochastic_Signals/Expected_Values_and_Moments|Expected Values and Moments]] can be used to determine the characteristics of the two random variables: |
:$$m_x=8/3 ,\hspace{0.5cm} \sigma_x=\sqrt{8/9},$$ | :$$m_x=8/3 ,\hspace{0.5cm} \sigma_x=\sqrt{8/9},$$ | ||
:$$ m_y= 3,\hspace{0.95cm} \sigma_y = \sqrt{\rm 2/3}.$$ | :$$ m_y= 3,\hspace{0.95cm} \sigma_y = \sqrt{\rm 2/3}.$$ | ||
| − | Due to the fact that the domain | + | Due to the fact that the definition domain $D$ is bounded by two straight lines $y_1(x)$ and $y_2(x)$ , the first order joint moment can be calculated here as follows. |
:$$m_{xy}={\rm E}\big[x\cdot y\big]=\int_{x_{1}}^{x_{2}}x\cdot \int_{y_{1}(x)}^{y_{2}(x)}y \cdot f_{xy}(x,y) \, \,{\rm d}y\, {\rm d}x.$$ | :$$m_{xy}={\rm E}\big[x\cdot y\big]=\int_{x_{1}}^{x_{2}}x\cdot \int_{y_{1}(x)}^{y_{2}(x)}y \cdot f_{xy}(x,y) \, \,{\rm d}y\, {\rm d}x.$$ | ||
| Line 35: | Line 35: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {What are the limit lines of the inner integral for $m_{xy}$ | + | {What are the limit lines of the inner integral for the $m_{xy}$ calculation? |
|type="()"} | |type="()"} | ||
- $y_1(x) = x+1, $ $y_2(x) = 2x+1.$ | - $y_1(x) = x+1, $ $y_2(x) = 2x+1.$ | ||
| Line 47: | Line 47: | ||
| − | {What is | + | {What is the covariance $\mu_{xy}$ ? |
|type="{}"} | |type="{}"} | ||
$\mu_{xy}\ = \ $ { 0.667 3% } | $\mu_{xy}\ = \ $ { 0.667 3% } | ||
| − | {What is | + | {What is the correlation coefficient $\rho_{xy}$? |
|type="{}"} | |type="{}"} | ||
$\rho_{xy}\ = \ $ { 0.866 3% } | $\rho_{xy}\ = \ $ { 0.866 3% } | ||
| − | {What is the equation of the correlation line $y = K(x)$ | + | {What is the equation of the correlation line $y = K(x)$? At what point $y_0$ does the straight line intersect the $y$–axis? <br>Show that the correlation line also passes through the point $(m_x, m_y)$. |
|type="{}"} | |type="{}"} | ||
$y_0\ = \ $ { 1 3% } | $y_0\ = \ $ { 1 3% } | ||
Revision as of 13:32, 7 February 2022
We consider the same random variable $(x, \ y)$ as in Exercise 4.1:
- In a domain defined by vertices $(0,\ 1)$, $(4,\ 3)$, and $(4,\ 5)$ let the 2D–PDF $f_{xy} (x, y) = 0.25$.
- There are no values outside this definition area $D$ marked in red in the graph.
Furthermore, the two marginal probability densities with respect to the quantities $x$ and $y$ are drawn in the graph, which have already been determined in Exercise 4.1.
From this, the equations of chapter Expected Values and Moments can be used to determine the characteristics of the two random variables:
- $$m_x=8/3 ,\hspace{0.5cm} \sigma_x=\sqrt{8/9},$$
- $$ m_y= 3,\hspace{0.95cm} \sigma_y = \sqrt{\rm 2/3}.$$
Due to the fact that the definition domain $D$ is bounded by two straight lines $y_1(x)$ and $y_2(x)$ , the first order joint moment can be calculated here as follows.
- $$m_{xy}={\rm E}\big[x\cdot y\big]=\int_{x_{1}}^{x_{2}}x\cdot \int_{y_{1}(x)}^{y_{2}(x)}y \cdot f_{xy}(x,y) \, \,{\rm d}y\, {\rm d}x.$$
Hints:
- The Exercise belongs to the chapter Two-Dimensional Random Variables.
- Reference is also made to the chapter Expected Values and Moments.
Questions
Solution
- Both $y_1(x)$ and $y_2(x)$ intersect the $y$-axis at $y= 1$.
- The lower boundary line has slope $0.5$, the upper has slope $1$.
(2) According to the clues we get:
- $$m_{xy}=\int_{\rm 0}^{\rm 4} x \cdot \int_{\it x/\rm 2 +\rm 1}^{\it x+\rm 1} {1}/{4}\cdot y \, \,{\rm d}y\,\, {\rm d}x = {1}/{8}\cdot \int_{\rm 0}^{\rm 4} x\cdot \big[( x+ 1)^{\rm 2}- ({ x}/{2}+1)^{\rm 2} \big] \,\, {\rm d}x. $$
- This leads to the integral or final result:
- $$m_{xy}={1}/{8}\int_{\rm 0}^{\rm 4}(\frac{3}{4}\cdot x^{3}{\rm +} x^2\,{\rm d}x = \rm \frac{1}{8} \cdot (\frac{3}{16}\cdot 4^4+\rm \frac{4^3}{3})=\frac{26}{3}\hspace{0.15cm}\underline{ \approx 8.667}.$$
(3) Since both random variables each have a nonzero mean, it follows für the covariance:
- $$\it \mu_{xy}=\it m_{xy}-m_{x}\cdot m_{y}=\frac{\rm 26}{\rm 3}-\frac{\rm 8}{\rm 3}\cdot\rm 3={2}/{3} \hspace{0.15cm}\underline{=0.667}.$$
(4) With the given rms we obtain:
- $$\rho_{xy}=\frac{\mu_{xy}}{\sigma_{x}\cdot\sigma_{y}}=\frac{{\rm 2}/{\rm 3}}{\sqrt{{\rm 8}/{\rm 9}}\cdot\sqrt{{\rm 2}/{\rm 3}}}=\sqrt{0.75}\hspace{0.15cm}\underline{=\rm 0.866}.$$
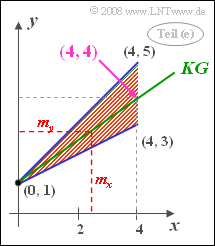
(5) For the correlation line (KG), in general:
- $$ y-m_{y}=\rho_{xy}\cdot\frac{\sigma_{y}}{\sigma_ {x}}\cdot(x-m_{x}).$$
- Using the numerical values calculated above, we obtain
- $$y={\rm 3}/{\rm 4}\cdot x +\rm 1.$$
The correlation line intersects the $y$-axis at $\underline{y=1}$ and also passes through the point $(4, 4)$. Any other result would also be impossible to interpret considering the definition area:
- If one sets $m_x = 8/3$ , one obtains $y = m_y = 3$.
- This means: The calculated correlation line actually passes through the point $(m_x, m_y)$, as the theory says.