Difference between revisions of "Aufgaben:Exercise 4.3: Algebraic and Modulo Sum"
| Line 3: | Line 3: | ||
}} | }} | ||
| − | [[File:EN_Sto_A_4_3.png|right|frame|Algebraic | + | [[File:EN_Sto_A_4_3.png|right|frame|Algebraic & modulo 2 sum]] |
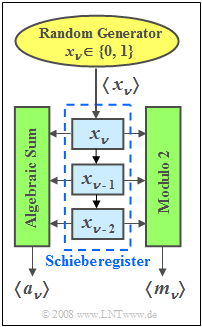
| − | A "clocked" random number generator returns a sequence $\langle x_\nu \rangle$ of binary random numbers. | + | A "clocked" random number generator returns a sequence $\langle x_\nu \rangle$ of binary random numbers. |
*It is assumed that the binary numbers $0$ and $1$ occur with equal probabilities and that the individual random numbers do not depend on each other. | *It is assumed that the binary numbers $0$ and $1$ occur with equal probabilities and that the individual random numbers do not depend on each other. | ||
*The random numbers $ x_\nu \in \{0, 1\}$ are entered into the first memory location of a shift register and shifted down one digit with each clock pulse. | *The random numbers $ x_\nu \in \{0, 1\}$ are entered into the first memory location of a shift register and shifted down one digit with each clock pulse. | ||
| Line 11: | Line 11: | ||
Two new random sequences $\langle a_\nu \rangle$ and $\langle m_\nu \rangle$ are formed from the contents of the three-digit shift register. Here denotes: | Two new random sequences $\langle a_\nu \rangle$ and $\langle m_\nu \rangle$ are formed from the contents of the three-digit shift register. Here denotes: | ||
| − | * | + | * the "algebraic sum" $a_\nu$: |
:$$a_\nu=x_\nu+x_{\nu-1}+x_{\nu-2},$$ | :$$a_\nu=x_\nu+x_{\nu-1}+x_{\nu-2},$$ | ||
| − | * | + | *the "modulo 2 sum" $m_\nu$: |
:$$m_\nu=x_\nu\oplus x_{\nu-1}\oplus x_{\nu-2}.$$ | :$$m_\nu=x_\nu\oplus x_{\nu-1}\oplus x_{\nu-2}.$$ | ||
| + | |||
| + | |||
| + | |||
| + | Hints: This exercise belongs to the chapter [[Theory_of_Stochastic_Signals/Two-Dimensional_Random_Variables|Two-Dimensional Random Variables]]. | ||
| + | |||
| + | |||
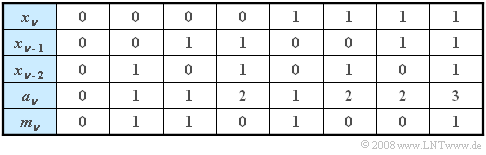
This fact is shown again in the following table: | This fact is shown again in the following table: | ||
[[File:P_ID254__Sto_A_4_3Tab.png|left|frame|Table for moment calculation]] | [[File:P_ID254__Sto_A_4_3Tab.png|left|frame|Table for moment calculation]] | ||
| − | + | ||
| − | + | ||
<br clear=all> | <br clear=all> | ||
===Questions=== | ===Questions=== | ||
Revision as of 14:48, 7 February 2022
A "clocked" random number generator returns a sequence $\langle x_\nu \rangle$ of binary random numbers.
- It is assumed that the binary numbers $0$ and $1$ occur with equal probabilities and that the individual random numbers do not depend on each other.
- The random numbers $ x_\nu \in \{0, 1\}$ are entered into the first memory location of a shift register and shifted down one digit with each clock pulse.
Two new random sequences $\langle a_\nu \rangle$ and $\langle m_\nu \rangle$ are formed from the contents of the three-digit shift register. Here denotes:
- the "algebraic sum" $a_\nu$:
- $$a_\nu=x_\nu+x_{\nu-1}+x_{\nu-2},$$
- the "modulo 2 sum" $m_\nu$:
- $$m_\nu=x_\nu\oplus x_{\nu-1}\oplus x_{\nu-2}.$$
Hints: This exercise belongs to the chapter Two-Dimensional Random Variables.
This fact is shown again in the following table:
Questions
Solution
- $${\rm Pr}(m_\nu = 0) = {\rm Pr}(m_\nu = 1)\hspace{0.15cm}\underline{=0.5}.$$
(2) The table shows that for each preassignment ⇒ $( x_{\nu-1}, x_{\nu-2}) = (0,0), (0,1), (1,0), (1,1)$ the values $m_\nu = 0$ respectively $m_\nu = 1$ are equally likely.
- Expressed differently: ${\rm Pr}(m_{\nu}\hspace{0.05cm}|\hspace{0.05cm}m_{\nu-1}) = {\rm Pr}( m_{\nu}).$
- This exactly matches the definition of "statistical independence" ⇒ Answer 1.
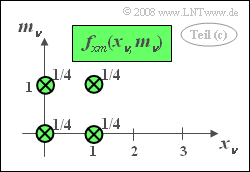
(3) Correct are the second and the last suggested solutions.
- The 2D PDF consists of four Dirac functions, each with weight $1/4$.
- One obtains this result, for example, by evaluating the table on the data page.
- Since $f_{xm}(x_\nu, m_\nu)$ is equal to the product $f_{x}(x_\nu) \cdot f_{m}(m_\nu)$ the quantities $x_\nu$ and $m_\nu$ are statistically independent.
- Statistically independent random variables, however, are also linearly statistically independent, so they are certainly uncorrelated.
(4) Within the sequence $\langle a_\nu \rangle$ of algebraic sum there are statistical bindings ⇒ Answer 2.
- You can see this because the unconditional probability $ {\rm Pr}( a_{\nu} = 0) =1/8$ is,
- while, for example ${\rm Pr}(a_{\nu} = 0\hspace{0.05cm}|\hspace{0.05cm}a_{\nu-1} = 3) =0$ holds.
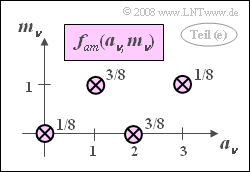
(5) Correct are the first and the last suggested solutions:
- As in the subtask (3) there are again four Dirac functions, but this time not with equal momentum weights $1/4$.
- The two-dimensional PDF thus cannot be written as a product of the two marginal probability densities.
- But this means that statistical bindings must exist between $a_\nu$ and $m_\nu$ .
- For the joint expected value, one obtains:
- $${\rm E}\big[a\cdot m \big] = \rm \frac{1}{8}\cdot 0 \cdot 0 +\frac{3}{8}\cdot 2 \cdot 0 +\frac{3}{8}\cdot 1 \cdot 1 + \frac{1}{8}\cdot 3 \cdot 1 = \frac{3}{4}.$$
- With the linear means ${\rm E}\big[a \big] = 1.5$ and ${\rm E}[m] = 0.5$ it thus follows for the covariance:
- $$\mu_{am}= {\rm E}\big[ a\cdot m \big] - {\rm E}\big[ a \big]\cdot {\rm E} \big[ m \big] = \rm 0.75-1.5\cdot 0.5 = \rm 0.$$
- Thus, the correlation coefficient $\rho_{am}= 0$. That is, The dependencies present are nonlinear.
- The quantities $a_\nu$ and $m_\nu$ are statistically dependent, but still uncorrelated.