Difference between revisions of "Theory of Stochastic Signals/Linear Combinations of Random Variables"
| Line 7: | Line 7: | ||
==Prerequisites and mean values== | ==Prerequisites and mean values== | ||
<br> | <br> | ||
| − | Throughout the chapter "Linear Combinations of Random Variables" we make the following assumptions: | + | Throughout the chapter "Linear Combinations of Random Variables" we make the following assumptions: |
*The random variables $u$ and $v$ are zero mean each ⇒ $m_u = m_v = 0$ and also statistically independent of each other ⇒ $ρ_{uv} = 0$. | *The random variables $u$ and $v$ are zero mean each ⇒ $m_u = m_v = 0$ and also statistically independent of each other ⇒ $ρ_{uv} = 0$. | ||
*The two random variables $u$ and $v$ each have equal standard deviation $σ$. No statement is made about the nature of the distribution. | *The two random variables $u$ and $v$ each have equal standard deviation $σ$. No statement is made about the nature of the distribution. | ||
| − | *Let the two random variables $x$ and $y$ be linear combinations of $u$ and $v$, where: | + | *Let the two random variables $x$ and $y$ be linear combinations of $u$ and $v$, where: |
:$$x=A \cdot u + B \cdot v + C,$$ | :$$x=A \cdot u + B \cdot v + C,$$ | ||
:$$y=D \cdot u + E \cdot v + F.$$ | :$$y=D \cdot u + E \cdot v + F.$$ | ||
| − | Thus, for the (linear) mean values of the new random variables $x$ and $y$ we obtain according to the general rules of calculation for expected values: | + | Thus, for the (linear) mean values of the new random variables $x$ and $y$ we obtain according to the general rules of calculation for expected values: |
:$$m_x =A \cdot m_u + B \cdot m_v + C =C,$$ | :$$m_x =A \cdot m_u + B \cdot m_v + C =C,$$ | ||
:$$m_y =D \cdot m_u + E \cdot m_v + F =F.$$ | :$$m_y =D \cdot m_u + E \cdot m_v + F =F.$$ | ||
| − | Thus, the coefficients $C$ and $F$ give only the mean values of $x$ and $y$ Both are always set to zero | + | Thus, the coefficients $C$ and $F$ give only the mean values of $x$ and $y$. Both are always set to zero on the following pages. |
==Resulting correlation coefficient== | ==Resulting correlation coefficient== | ||
<br> | <br> | ||
| Line 24: | Line 24: | ||
:$$\sigma _x ^2 = {\rm E}\big[x ^{\rm 2}\big] = A^{\rm 2} \cdot {\rm E}\big[u^{\rm 2}\big] + B^{\rm 2} \cdot {\rm E}\big[v^{\rm 2}\big] + {\rm 2} \cdot A \cdot B \cdot {\rm E}\big[u \cdot v\big].$$ | :$$\sigma _x ^2 = {\rm E}\big[x ^{\rm 2}\big] = A^{\rm 2} \cdot {\rm E}\big[u^{\rm 2}\big] + B^{\rm 2} \cdot {\rm E}\big[v^{\rm 2}\big] + {\rm 2} \cdot A \cdot B \cdot {\rm E}\big[u \cdot v\big].$$ | ||
| − | *The expected values of $u^2$ and $v^2$ are by definition equal to $σ^2$, | + | *The expected values of $u^2$ and $v^2$ are by definition equal to $σ^2$, because $u$ and $v$ are zero mean. |
| − | *Since $u$ and $v$ are moreover assumed to be statistically independent, one can | + | *Since $u$ and $v$ are moreover assumed to be statistically independent, one can write for the expected value of the product: |
:$${\rm E}\big[u \cdot v\big] = {\rm E}\big[u\big] \cdot {\rm E}\big[v\big] = m_u \cdot m_v = \rm 0.$$ | :$${\rm E}\big[u \cdot v\big] = {\rm E}\big[u\big] \cdot {\rm E}\big[v\big] = m_u \cdot m_v = \rm 0.$$ | ||
| − | *Thus, for the variances of the random variables formed by linear combinations, we obtain: | + | *Thus, for the variances of the random variables formed by linear combinations, we obtain: |
:$$\sigma _x ^2 =(A^2 + B^2) \cdot \sigma ^2,$$ | :$$\sigma _x ^2 =(A^2 + B^2) \cdot \sigma ^2,$$ | ||
:$$\sigma _y ^2 =(D^2 + E^2) \cdot \sigma ^2.$$ | :$$\sigma _y ^2 =(D^2 + E^2) \cdot \sigma ^2.$$ | ||
| − | The '''covariance''' $μ_{xy}$ is identical to the joint moment $m_{xy}$ for zero mean random variables $x$ and $y$ ⇒ $C = F = 0$ | + | The '''covariance''' $μ_{xy}$ is identical to the joint moment $m_{xy}$ for zero mean random variables $x$ and $y$ ⇒ $C = F = 0$: |
:$$\mu_{xy } = m_{xy } = {\rm E}\big[x \cdot y\big] = {\rm E}\big[(A \cdot u + B \cdot v)\cdot (D \cdot u + E \cdot v)\big].$$ | :$$\mu_{xy } = m_{xy } = {\rm E}\big[x \cdot y\big] = {\rm E}\big[(A \cdot u + B \cdot v)\cdot (D \cdot u + E \cdot v)\big].$$ | ||
| − | Note here that ${\rm E}\big[ \text{...} \big]$ denotes an expected value, while $E$ describes a | + | Note here that ${\rm E}\big[ \text{...} \big]$ denotes an expected value, while $E$ describes a coefficient. |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Conclusion:}$ After evaluating this equation in an analogous manner to above, it follows: | + | $\text{Conclusion:}$ After evaluating this equation in an analogous manner to above, it follows: |
:$$\mu_{xy } = (A \cdot D + B \cdot E) \cdot \sigma^{\rm 2 } | :$$\mu_{xy } = (A \cdot D + B \cdot E) \cdot \sigma^{\rm 2 } | ||
| − | \hspace{0.3cm}\ | + | \hspace{0.3cm}\Rightarrow\hspace{0.3cm} |
\rho_{xy } = \frac{\rho_{xy } }{\sigma_x \cdot \sigma_y} = \frac {A \cdot D + B \cdot E}{\sqrt{(A^{\rm 2}+B^{\rm 2})(D^{\rm 2}+E^{\rm 2} ) } }. $$}} | \rho_{xy } = \frac{\rho_{xy } }{\sigma_x \cdot \sigma_y} = \frac {A \cdot D + B \cdot E}{\sqrt{(A^{\rm 2}+B^{\rm 2})(D^{\rm 2}+E^{\rm 2} ) } }. $$}} | ||
We now exclude two special cases: | We now exclude two special cases: | ||
| − | *$A = B = 0$ ⇒ $x ≡ 0$ | + | *$A = B = 0$ ⇒ $x ≡ 0$, |
*$D = E = 0$ ⇒ $y ≡ 0$. | *$D = E = 0$ ⇒ $y ≡ 0$. | ||
| Line 52: | Line 52: | ||
$\text{Example 1:}$ | $\text{Example 1:}$ | ||
If we set $A = E = 0$, we get the correlation coefficient $ρ_{xy} = 0$. This result is insightful: | If we set $A = E = 0$, we get the correlation coefficient $ρ_{xy} = 0$. This result is insightful: | ||
| − | *Now $x$ depends only on $v$ and $y$ depends exclusively on $u$ | + | *Now $x$ depends only on $v$ and $y$ depends exclusively on $u$. |
| − | *But since $u$ and $v$ were assumed to be statistically independent, there are also no relationships between $x$ and $y$. | + | *But since $u$ and $v$ were assumed to be statistically independent, there are also no relationships between $x$ and $y$. |
| − | *Similarly, $ρ_{xy} = 0$ results for the combination $B = D = 0$.}} | + | *Similarly, $ρ_{xy} = 0$ results for the combination $B = D = 0$.}} |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{Example 2:}$ The constellation $B = E = 0$ leads to the fact that both $x$ and $y$ depend only on $u$ Then the correlation coefficient is obtained: | + | $\text{Example 2:}$ The constellation $B = E = 0$ leads to the fact that both $x$ and $y$ depend only on $u$. Then the following correlation coefficient is obtained: |
:$$\rho_{xy } = \frac {A \cdot D }{\sqrt{A^{\rm 2}\cdot D^{\rm 2} } } = \frac {A \cdot D }{\vert A\vert \cdot D\vert } =\pm 1. $$ | :$$\rho_{xy } = \frac {A \cdot D }{\sqrt{A^{\rm 2}\cdot D^{\rm 2} } } = \frac {A \cdot D }{\vert A\vert \cdot D\vert } =\pm 1. $$ | ||
| − | *If $A$ and $D$ have the same sign, then $ρ_{xy} = +1$. | + | *If $A$ and $D$ have the same sign, then $ρ_{xy} = +1$. |
| − | *For different signs, the correlation coefficient is $-1$. | + | *For different signs, the correlation coefficient is $-1$. |
| − | *Also | + | *Also for $A = D = 0:$ The coefficient $ρ_{xy} = ±1$, if $B \ne 0$ and $E \ne 0$ holds. }} |
==Generation of correlated random variables== | ==Generation of correlated random variables== | ||
<br> | <br> | ||
| − | The [[Theory_of_Stochastic_Signals/Linear_Combinations_of_Random_Variables#Resulting_correlation_coefficient|previously used equations]] can be used to generate a two-dimensional random variable $(x, y)$ with given characteristics $σ_x$, $σ_y$ and $ρ_{xy}$ | + | The [[Theory_of_Stochastic_Signals/Linear_Combinations_of_Random_Variables#Resulting_correlation_coefficient|previously used equations]] can be used to generate a two-dimensional random variable $(x,\hspace{0.08cm} y)$ with given characteristics $σ_x$, $σ_y$ and $ρ_{xy}$. |
*If no further preconditions are met other than these three nominal values, one of the four coefficients $A, \ B, \ D$ and $E$ is arbitrary. | *If no further preconditions are met other than these three nominal values, one of the four coefficients $A, \ B, \ D$ and $E$ is arbitrary. | ||
| Line 77: | Line 77: | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
$\text{Example 3:}$ | $\text{Example 3:}$ | ||
| − | We always assume zero mean Gaussian random variables $u$ and $v$ Both have variance $σ^2 = 1$. | + | We always assume zero mean Gaussian random variables $u$ and $v$. Both have variance $σ^2 = 1$. |
| − | $(1)$ To generate a | + | $(1)$ To generate a two-dimensional random variable with desired characteristics $σ_x =1$, $σ_y = 1.55$ and $ρ_{xy} = -0.8$ the parameter set is suitable, for example: |
| − | [[File:P_ID419__Sto_T_4_3_S3_neu.png|right |frame| | + | [[File:P_ID419__Sto_T_4_3_S3_neu.png|right |frame| Two-dimensional random variables generated by linear combination]] |
:$$A = -0.8, \; B = 0.6, \; D = 1.55, \; E = 0.$$ | :$$A = -0.8, \; B = 0.6, \; D = 1.55, \; E = 0.$$ | ||
| − | *This set | + | *This parameter set underlies the left graph. |
| − | *The regression line $ | + | *The regression line $(\rm RL)$ is shown in red. |
*It runs at an angle of about $-50^\circ$. | *It runs at an angle of about $-50^\circ$. | ||
*Drawn in purple is the ellipse major axis, which lies slightly above the regression line. | *Drawn in purple is the ellipse major axis, which lies slightly above the regression line. | ||
| Line 91: | Line 91: | ||
$(2)$ The parameter set for the right graph is: | $(2)$ The parameter set for the right graph is: | ||
:$$A = -0.625,\; B = 0.781,\; D = 1.501,\; E = -0.390.$$ | :$$A = -0.625,\; B = 0.781,\; D = 1.501,\; E = -0.390.$$ | ||
| − | *In a statistical sense, the same result is obtained even though the two point clouds differ in detail. | + | *In a statistical sense, the same result is obtained even though the two point clouds differ in detail. |
| − | * | + | *With respect to regression line $(\rm RL)$ and ellipse major axis $(\rm EA)$, there is no difference with respect to the parameter set $(1)$. }} |
==Exercises for the chapter== | ==Exercises for the chapter== | ||
Revision as of 13:36, 25 February 2022
Contents
Prerequisites and mean values
Throughout the chapter "Linear Combinations of Random Variables" we make the following assumptions:
- The random variables $u$ and $v$ are zero mean each ⇒ $m_u = m_v = 0$ and also statistically independent of each other ⇒ $ρ_{uv} = 0$.
- The two random variables $u$ and $v$ each have equal standard deviation $σ$. No statement is made about the nature of the distribution.
- Let the two random variables $x$ and $y$ be linear combinations of $u$ and $v$, where:
- $$x=A \cdot u + B \cdot v + C,$$
- $$y=D \cdot u + E \cdot v + F.$$
Thus, for the (linear) mean values of the new random variables $x$ and $y$ we obtain according to the general rules of calculation for expected values:
- $$m_x =A \cdot m_u + B \cdot m_v + C =C,$$
- $$m_y =D \cdot m_u + E \cdot m_v + F =F.$$
Thus, the coefficients $C$ and $F$ give only the mean values of $x$ and $y$. Both are always set to zero on the following pages.
Resulting correlation coefficient
Let us now consider the variances of the random variables according to the linear combinations.
- For the random variable $x$ holds independently of the parameter $C$:
- $$\sigma _x ^2 = {\rm E}\big[x ^{\rm 2}\big] = A^{\rm 2} \cdot {\rm E}\big[u^{\rm 2}\big] + B^{\rm 2} \cdot {\rm E}\big[v^{\rm 2}\big] + {\rm 2} \cdot A \cdot B \cdot {\rm E}\big[u \cdot v\big].$$
- The expected values of $u^2$ and $v^2$ are by definition equal to $σ^2$, because $u$ and $v$ are zero mean.
- Since $u$ and $v$ are moreover assumed to be statistically independent, one can write for the expected value of the product:
- $${\rm E}\big[u \cdot v\big] = {\rm E}\big[u\big] \cdot {\rm E}\big[v\big] = m_u \cdot m_v = \rm 0.$$
- Thus, for the variances of the random variables formed by linear combinations, we obtain:
- $$\sigma _x ^2 =(A^2 + B^2) \cdot \sigma ^2,$$
- $$\sigma _y ^2 =(D^2 + E^2) \cdot \sigma ^2.$$
The covariance $μ_{xy}$ is identical to the joint moment $m_{xy}$ for zero mean random variables $x$ and $y$ ⇒ $C = F = 0$:
- $$\mu_{xy } = m_{xy } = {\rm E}\big[x \cdot y\big] = {\rm E}\big[(A \cdot u + B \cdot v)\cdot (D \cdot u + E \cdot v)\big].$$
Note here that ${\rm E}\big[ \text{...} \big]$ denotes an expected value, while $E$ describes a coefficient.
$\text{Conclusion:}$ After evaluating this equation in an analogous manner to above, it follows:
- $$\mu_{xy } = (A \cdot D + B \cdot E) \cdot \sigma^{\rm 2 } \hspace{0.3cm}\Rightarrow\hspace{0.3cm} \rho_{xy } = \frac{\rho_{xy } }{\sigma_x \cdot \sigma_y} = \frac {A \cdot D + B \cdot E}{\sqrt{(A^{\rm 2}+B^{\rm 2})(D^{\rm 2}+E^{\rm 2} ) } }. $$
We now exclude two special cases:
- $A = B = 0$ ⇒ $x ≡ 0$,
- $D = E = 0$ ⇒ $y ≡ 0$.
Then the above equation always yields unique values for the correlation coefficient in the range $-1 ≤ ρ_{xy} ≤ +1$.
$\text{Example 1:}$ If we set $A = E = 0$, we get the correlation coefficient $ρ_{xy} = 0$. This result is insightful:
- Now $x$ depends only on $v$ and $y$ depends exclusively on $u$.
- But since $u$ and $v$ were assumed to be statistically independent, there are also no relationships between $x$ and $y$.
- Similarly, $ρ_{xy} = 0$ results for the combination $B = D = 0$.
$\text{Example 2:}$ The constellation $B = E = 0$ leads to the fact that both $x$ and $y$ depend only on $u$. Then the following correlation coefficient is obtained:
- $$\rho_{xy } = \frac {A \cdot D }{\sqrt{A^{\rm 2}\cdot D^{\rm 2} } } = \frac {A \cdot D }{\vert A\vert \cdot D\vert } =\pm 1. $$
- If $A$ and $D$ have the same sign, then $ρ_{xy} = +1$.
- For different signs, the correlation coefficient is $-1$.
- Also for $A = D = 0:$ The coefficient $ρ_{xy} = ±1$, if $B \ne 0$ and $E \ne 0$ holds.
The previously used equations can be used to generate a two-dimensional random variable $(x,\hspace{0.08cm} y)$ with given characteristics $σ_x$, $σ_y$ and $ρ_{xy}$.
- If no further preconditions are met other than these three nominal values, one of the four coefficients $A, \ B, \ D$ and $E$ is arbitrary.
- In the following, we always arbitrarily set $E = 0$ .
- With the further specification that the statistically independent random variables $u$ and $v$ each have standard deviation $σ =1$ we obtain:
- $$D = \sigma_y, \hspace{0.5cm} A = \sigma_x \cdot \rho_{xy}, \hspace{0.5cm} B = \sigma_x \cdot \sqrt {1-\rho_{xy}^2}.$$
- For $σ ≠ 1$ these values must still be divided by $σ$ in each case.
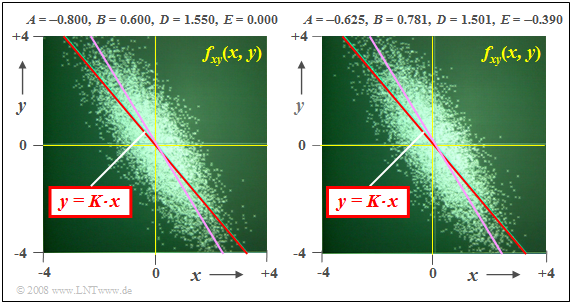
$\text{Example 3:}$ We always assume zero mean Gaussian random variables $u$ and $v$. Both have variance $σ^2 = 1$.
$(1)$ To generate a two-dimensional random variable with desired characteristics $σ_x =1$, $σ_y = 1.55$ and $ρ_{xy} = -0.8$ the parameter set is suitable, for example:
- $$A = -0.8, \; B = 0.6, \; D = 1.55, \; E = 0.$$
- This parameter set underlies the left graph.
- The regression line $(\rm RL)$ is shown in red.
- It runs at an angle of about $-50^\circ$.
- Drawn in purple is the ellipse major axis, which lies slightly above the regression line.
$(2)$ The parameter set for the right graph is:
- $$A = -0.625,\; B = 0.781,\; D = 1.501,\; E = -0.390.$$
- In a statistical sense, the same result is obtained even though the two point clouds differ in detail.
- With respect to regression line $(\rm RL)$ and ellipse major axis $(\rm EA)$, there is no difference with respect to the parameter set $(1)$.
Exercises for the chapter
Exercise 4.7: Weighted Sum and Difference
Exercise 4.7Z: Generation of a "2D-PDF"
Exercise 4.8: Diamond shaped "2D-PDF"