Aufgaben:Exercise 4.7: Weighted Sum and Difference

• Return to book

Sum and difference of random variables

Let the random variables  $u$  and  $v$  be statistically independent of each other, each with mean  $m$  and variance  $\sigma^2$.

• Both variables have equal PDF and CDF.
• Nothing is known about the course of these functions for the time being.

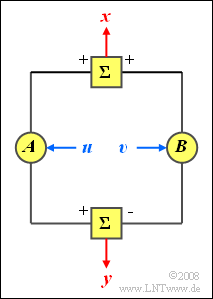
Now two new random variables  $x$  and  $y$  are formed according to the following equations:

$$x = A \cdot u + B \cdot v,$$

$$y= A \cdot u - B \cdot v.$$

Here  $A$  and  $B$  denote (any) constant values.

• For the subtasks  (1)  to  (4)  let   $m= 0$,   $\sigma = 1$,   $A = 1$  and  $B = 2$.
• In the sub-task  (6)'  it is assumed that  $u$  and  $v$  are each uniformly distributed with mean  $m= 1$  and standard deviation  $\sigma = 0.5$  . For the constants, $A = B = 1$.
• For the exercise  (7)  it is still valid  $A = B = 1$.  Here the random variables  $u$  and  $v$  are symmetrically two-point distributed on  $\pm$1:

$${\rm Pr}(u=+1) = {\rm Pr}(u=-1) = {\rm Pr}(v=+1) = {\rm Pr}(v=-1) =0.5.$$

Note:

• The exercise belongs to the chapter  Linear Combinations of Random Variables.

Questions

1

What is the mean and standard deviation of  $x$  for  $A = 1$  and  $B = 2$?

$m_x \ = \ $

$\sigma_x \ = \ $

2

What is the mean and standard deviation of  $y$  for  $A = 1$  and  $B = 2$?

$m_y \ = \ $

$\sigma_y \ = \ $

3

Calculate the covariance  $\mu_{xy}$.  What value results for  $A = 1$  and  $B = 2$?

$\mu_{xy} \ = \ $

4

Calculate the correlation coefficient  $\rho_{xy}$  as a function of the quotient  $B/A$.  What coefficient results for  $A = 1$  and  $B = 2$?

$\rho_{xy}\ = \ $

5

Which of the following statements is always true?

	For  $B = 0$  the random variables  $x$  and  $y$  are strictly correlated.
	It holds  $\rho_{xy}(-B/A) = -\rho_{xy}(B/A)$.
	In the limiting case  $B/A \to \infty$  the random variables  $x$  and  $y$  are strictly correlated.
	For  $A =B$  the random variables $x$  and  $y$  are uncorrelated.

6

Which statements are true if  $A =B = 1$  holds and  $x$  and  $y$  are each gauged;distributed with mean  $m = 1$  and standard deviation  $\sigma = 0.5$ ?

	The random variables $x$  and  $y$  are uncorrelated.
	The random variables $x$  and  $y$  are statistically independent.

7

Which statements are true if  $x$  and  $y$  are symmetrically two-point distributed and  $A =B = 1$  holds?

	The random variables $x$  and  $y$  are uncorrelated.
	The random variables $x$  and  $y$  are statistically independent.

Solution

Solution

(1)  Since the random variables  $u$  and  $v$  are zero mean  $(m = 0)$, the random variable  $x$  is also zero mean:

$$m_x = (A +B) \cdot m \hspace{0.15cm}\underline{ =0}.$$

• For the variance and standard deviation:

$$\sigma_x^2 = (A^2 +B^2) \cdot \sigma^2 = 5; \hspace{0.5cm} \sigma_x = \sqrt{5}\hspace{0.15cm}\underline{ \approx 2.236}.$$

(2)  Since  $u$  and  $v$  have the same standard deviation, so does  $\sigma_y =\sigma_x \hspace{0.15cm}\underline{ \approx 2.236}$.

• Because  $m=0$  also  $m_y = m_x \hspace{0.15cm}\underline{ =0}.$.
• For mean-valued random variable  $u$  and  $v$  on the other hand, for  $m_y = (A -B) \cdot m$  adds up to a different value than for  $m_x = (A +B) \cdot m$.

(3)  We assume here in the sample solution the more general case  $m \ne 0$  Then for the common moment holds:

$$m_{xy} = {\rm E} \big[x \cdot y \big] = {\rm E} \big[(A \cdot u + B \cdot v) (A \cdot u - B \cdot v)\big] . $$

• According to the general calculation rules for expected values, it follows:

$$m_{xy} = A^2 \cdot {\rm E} \big[u^2 \big] - B^2 \cdot {\rm E} \big[v^2 \big] = (A^2 - B^2)(m^2 + \sigma^2).$$

• This gives the covariance to.

$$\mu_{xy} = m_{xy} - m_{x} \cdot m_{y}= (A^2 - B^2)(m^2 + \sigma^2) - (A + B)(A-B) \cdot m^2 = (A^2 - B^2) \cdot \sigma^2.$$

• With  $\sigma = 1$,  $A = 1$  and  $B = 2$  we get  $\mu_{xy} \hspace{0.15cm}\underline{ =-3}$  and this is independent of the mean  $m$  of the variables  $u$  and  $v$.

correlation coefficient as a function of quotient  $B/A$

(4)  The correlation coefficient is obtained as.

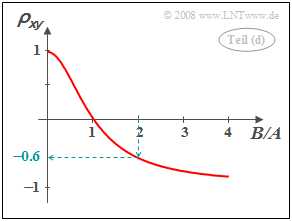
$$\rho_{xy} =\frac{\mu_{xy}}{\sigma_x \cdot \sigma_y} = \frac{(A^2 - B^2) \cdot \sigma^2}{(A^2 +B^2) \cdot \sigma^2} \hspace{0.5 cm}\rightarrow \hspace{0.5 cm}\rho_{xy} =\frac{1 - (B/A)^2} {1 +(B/A)^2}.$$

• With  $B/A = 2$  it follows  $\rho_{xy} \hspace{0.15cm}\underline{ =-0.6}$.

(5)  Correct are statements 1, 3, and 4:

• From  $B= 0$  follows  $\rho_{xy} = 1$  (strict correlation).  It can be further seen that in this case  $x = u$  and  $y = u$  are identical random variables.
• The second statement is not true:   For  $A = 1$  and  $B= -2$  also results  $\rho_{xy} = -0.6$.
• So the sign of the quotient does not matter because in the equation calculated in subtask  (4)'  the quotient  $B/A$  occurs only quadratically.
• If  $B \gg A$, both  $x$  and  $y$  are determined almost exclusively by the random variableö&ahead;e  $v$  and it is  $ y \approx -x$.  This corresponds to the correlation coefficient  $\rho_{xy} = -1$.
• In contrast,  $B/A = 1$  always yields the correlation coefficient  $\rho_{xy} = 0$  and thus the uncorrelatedness between  $x$  and  $y$.

(6)  Both statements correct are true:

• When  $A=B$  are  $x$  and  $y$  always  $($so for any PDF of the variables $u$  and  $v)$  uncorrelated.
• The new random variables  $x$  and  $y$  are therefore also distributed randomly.
• For Gaussian randomness, however, statistical independence follows from uncorrelatedness, and vice versa.

2D-PDF and Edge-PDF

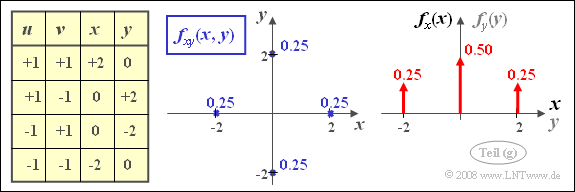
(7)  Here, only statement 1 is true:

• The correlation coefficient results with  $A=B= 1$  also here to  $\rho_{xy} = 0$.  That is:  $x$  and  $y$  are uncorrelated also here.
• On the other hand, it can be seen from the sketched two dimensional PDF that the condition of statistical independence no longer applies in the present case:

$$f_{xy}(x, y) \ne f_{x}(x) \cdot f_{y}(y).$$