Difference between revisions of "Aufgaben:Exercise 4.09Z: Periodic ACF"
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Theory_of_Stochastic_Signals/Auto-Correlation_Function |
}} | }} | ||
| − | [[File:P_ID380__Sto_Z_4_9.png|right|frame| | + | [[File:P_ID380__Sto_Z_4_9.png|right|frame|Periodic multistage rectangular signal]] |
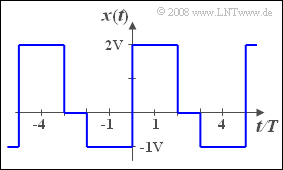
| − | + | We consider in this exercise a periodic and simultaneously ergodic stochastic process $\{x_i(t)\}$, which is fully characterized by the presented pattern function $x(t)$ . | |
| − | + | Further pattern signals of the random process $\{x_i(t)\}$ are obtained by shifting by delays of different sizes $\tau_i$, where $\tau_i$ is assumed to be uniformly distributed between $0$ and the period $T_0$ . | |
| Line 14: | Line 14: | ||
| − | + | Hint: | |
| − | * | + | *The exercise belongs to the chapter [[Theory_of_Stochastic_Signals/Auto-Correlation_Function|Auto-Correlation Function]]. |
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Determine the period duration $T_0$ normalized to the period duration $T$ defined in the sketch. |
|type="{}"} | |type="{}"} | ||
| − | $T_0/T \ = \ $ | + | $T_0/T \ = \ $ { 5 3% } |
| − | { | + | {What is the size of the DC signal component (linear mean) $m_x$ of the described process $\{x_i(t)\}$? |
|type="{}"} | |type="{}"} | ||
$m_x \ = \ $ { 0.4 3% } $\ \rm V$ | $m_x \ = \ $ { 0.4 3% } $\ \rm V$ | ||
| − | { | + | {What is the process power (related to the resistor $1 \hspace{0.05cm} \rm \Omega$ )? |
|type="{}"} | |type="{}"} | ||
$P_x \ = \ $ { 2 3% } $\ \rm V^2$ | $P_x \ = \ $ { 2 3% } $\ \rm V^2$ | ||
| − | { | + | {Calculate the ASF values für $\tau = T$ and $\tau = 2T$. |
|type="{}"} | |type="{}"} | ||
$\varphi_x(\tau = T) \ = \ $ { 0.6 3% } $\ \rm V^2$ | $\varphi_x(\tau = T) \ = \ $ { 0.6 3% } $\ \rm V^2$ | ||
| Line 43: | Line 43: | ||
| − | { | + | {Sketch the ACF curve taking into account symmetries. What values result for $\tau = 3T$ and $\tau = 4T$? |
|type="{}"} | |type="{}"} | ||
$\varphi_x(\tau = 3T) \ = \ $ { -1.236--1.164 } $\ \rm V^2$ | $\varphi_x(\tau = 3T) \ = \ $ { -1.236--1.164 } $\ \rm V^2$ | ||
| Line 49: | Line 49: | ||
| − | { | + | {Calculate the expected value of the ACF with respect to all $\tau$ values. Interpret the result. |
|type="{}"} | |type="{}"} | ||
${\rm E}\big[\varphi_x(\tau)\big]\ = \ $ { 0.16 3% } $\ \rm V^2$ | ${\rm E}\big[\varphi_x(\tau)\big]\ = \ $ { 0.16 3% } $\ \rm V^2$ | ||
| Line 56: | Line 56: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | [[File:P_ID382__Sto_Z_4_9_d.png|right|frame| | + | [[File:P_ID382__Sto_Z_4_9_d.png|right|frame|For ACF–calculation]] |
| − | '''(1)''' | + | '''(1)''' The (normalized) period duration is $T_0/T \hspace{0.15cm}\underline{= 5}.$ |
| − | '''(2)''' | + | '''(2)''' Due to periodicity, the averaging üg over a periodic time $T_0$: |
| − | :$$m_x = \frac{1}{T_0} \cdot \int_0^{T_0} x(t) \hspace{0.1cm}{\rm d} | + | :$$m_x = \frac{1}{T_0} \cdot \int_0^{T_0} x(t) \hspace{0.1cm}{\rm d} t = \frac{1}{5 T} \cdot (2\hspace{0.05cm}{\rm V} \cdot 2 T - 2\hspace{0.05cm}{\rm V} \cdot 2 T) \hspace{0.15cm}\underline{= \rm 0.4 \,V}.$$ |
| − | '''(3)''' In | + | '''(3)''' In analogy to the last sub-task, we obtain for the mean power: |
| − | :$$P_x = | + | :$$P_x = \frac{2 T}{5 T} \cdot \big[(\rm 2V)^2 +(- \rm 1V)^2 \big]\hspace{0.15cm}\underline{ = \rm 2 \,V^2}.$$ |
| − | '''(4)''' | + | '''(4)''' The accompanying graph shows in each case in the range from $0$ to $T_0 = 5T$. |
| − | * | + | *above the product $x(t) \cdot x(t+T)$, |
| − | * | + | *down the product $x(t) \cdot x(t+2T)$. |
| − | + | Note that $x(t+T)$ means a shift of the signal $x(t)$ by $T$ to the left. | |
| − | + | From these sketches follow the relations: | |
| − | :$$\varphi_x (T)= | + | :$$\varphi_x (T)= \rm {1}/{5 } \cdot (\rm 4V^2 + \rm 1V^2 - \rm 2V^2) \hspace{0.15cm}\underline{= \rm 0.6\, V^2},$$ |
| − | :$$\varphi_x ( 2 T)= | + | :$$\varphi_x ( 2 T)= \rm {1}/{5 } \cdot(-\rm 2V^2 \cdot 3) \hspace{0.15cm}\underline{= - \rm 1.2 \,V^2}.$$ |
| − | '''(5)''' | + | '''(5)''' An auto-correlation function is always even: $\varphi_x (-\tau)= \varphi_x (\tau)$. |
| − | * | + | *In addition, for periodic processes, the ACF is also periodic with the same periodic time $T_0$ as the individual pattern functions. It follows that: |
| − | [[File:P_ID383__Sto_Z_4_9_e.png|right|frame| | + | [[File:P_ID383__Sto_Z_4_9_e.png|right|frame|Sought auto-correlation function]] |
| − | :$$\varphi_x ( 0) = | + | :$$\varphi_x ( 0) = \varphi_x (5 T) = \varphi_x (10 T) = \ \text{...} \ = \it P_x = \rm 2 \,V^2,$$ |
| − | :$$\varphi_x (3 T) = \varphi_x (-3 T) =\varphi_x (2 T) = \ \text{...} \ | + | :$$\varphi_x (3 T) = \varphi_x (-3 T) =\varphi_x (2 T) = \ \text{...} \ \hspace{0.15cm}\underline{= - \rm 1.2 \,V^2},$$ |
| − | :$$\varphi_x (4 T) = \varphi_x (-4 T) =\varphi_x ( T) = \ \text{...} \ | + | :$$\varphi_x (4 T) = \varphi_x (-4 T) =\varphi_x ( T) = \ \text{...} \ \hspace{0.15cm}\underline{= \rm 0.6 \,V^2}.$$ |
| − | * | + | *The calculated ACF values can be connected by straight line sections, since integration üover rectangular functions always yields linear subsections. |
| − | '''(6)''' | + | '''(6)''' The five intervals $(0$ to $T)$, $(T$ to $2T)$, ... , $(4T$ to $5T)$ provide the contributions. |
| − | :$$(+1.3; | + | :$$(+1.3; -0.3; -1.2; -0.3; +1.3) \cdot \rm V^2.$$ |
| − | * | + | *This gives the expected value (linear mean): |
| − | :$${\rm E}\big[\varphi_x(\tau)\big] = 1/5 \cdot (1.3-0.3 -1.2 -0.3 +1.3]\hspace{0.15cm}\underline{= | + | :$${\rm E}\big[\varphi_x(\tau)\big] = 1/5 \cdot (1.3-0.3 -1.2 -0.3 +1.3]\hspace{0.15cm}\underline{= \rm 0.16 \,V^2}.$$ |
| − | * | + | *This corresponds to the square of the mean $m_x$ ⇒ see subtask '''(2)'''. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Revision as of 18:31, 28 February 2022
We consider in this exercise a periodic and simultaneously ergodic stochastic process $\{x_i(t)\}$, which is fully characterized by the presented pattern function $x(t)$ .
Further pattern signals of the random process $\{x_i(t)\}$ are obtained by shifting by delays of different sizes $\tau_i$, where $\tau_i$ is assumed to be uniformly distributed between $0$ and the period $T_0$ .
Hint:
- The exercise belongs to the chapter Auto-Correlation Function.
Questions
Solution
(1) The (normalized) period duration is $T_0/T \hspace{0.15cm}\underline{= 5}.$
(2) Due to periodicity, the averaging üg over a periodic time $T_0$:
- $$m_x = \frac{1}{T_0} \cdot \int_0^{T_0} x(t) \hspace{0.1cm}{\rm d} t = \frac{1}{5 T} \cdot (2\hspace{0.05cm}{\rm V} \cdot 2 T - 2\hspace{0.05cm}{\rm V} \cdot 2 T) \hspace{0.15cm}\underline{= \rm 0.4 \,V}.$$
(3) In analogy to the last sub-task, we obtain for the mean power:
- $$P_x = \frac{2 T}{5 T} \cdot \big[(\rm 2V)^2 +(- \rm 1V)^2 \big]\hspace{0.15cm}\underline{ = \rm 2 \,V^2}.$$
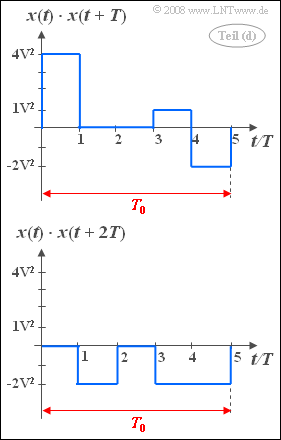
(4) The accompanying graph shows in each case in the range from $0$ to $T_0 = 5T$.
- above the product $x(t) \cdot x(t+T)$,
- down the product $x(t) \cdot x(t+2T)$.
Note that $x(t+T)$ means a shift of the signal $x(t)$ by $T$ to the left.
From these sketches follow the relations:
- $$\varphi_x (T)= \rm {1}/{5 } \cdot (\rm 4V^2 + \rm 1V^2 - \rm 2V^2) \hspace{0.15cm}\underline{= \rm 0.6\, V^2},$$
- $$\varphi_x ( 2 T)= \rm {1}/{5 } \cdot(-\rm 2V^2 \cdot 3) \hspace{0.15cm}\underline{= - \rm 1.2 \,V^2}.$$
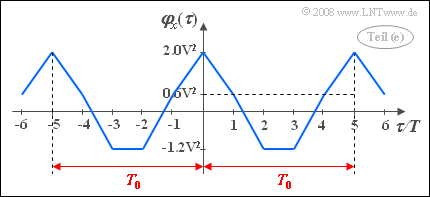
(5) An auto-correlation function is always even: $\varphi_x (-\tau)= \varphi_x (\tau)$.
- In addition, for periodic processes, the ACF is also periodic with the same periodic time $T_0$ as the individual pattern functions. It follows that:
- $$\varphi_x ( 0) = \varphi_x (5 T) = \varphi_x (10 T) = \ \text{...} \ = \it P_x = \rm 2 \,V^2,$$
- $$\varphi_x (3 T) = \varphi_x (-3 T) =\varphi_x (2 T) = \ \text{...} \ \hspace{0.15cm}\underline{= - \rm 1.2 \,V^2},$$
- $$\varphi_x (4 T) = \varphi_x (-4 T) =\varphi_x ( T) = \ \text{...} \ \hspace{0.15cm}\underline{= \rm 0.6 \,V^2}.$$
- The calculated ACF values can be connected by straight line sections, since integration üover rectangular functions always yields linear subsections.
(6) The five intervals $(0$ to $T)$, $(T$ to $2T)$, ... , $(4T$ to $5T)$ provide the contributions.
- $$(+1.3; -0.3; -1.2; -0.3; +1.3) \cdot \rm V^2.$$
- This gives the expected value (linear mean):
- $${\rm E}\big[\varphi_x(\tau)\big] = 1/5 \cdot (1.3-0.3 -1.2 -0.3 +1.3]\hspace{0.15cm}\underline{= \rm 0.16 \,V^2}.$$
- This corresponds to the square of the mean $m_x$ ⇒ see subtask (2).