Difference between revisions of "Aufgaben:Exercise 4.13: Gaussian ACF and PSD"
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Theory_of_Stochastic_Signals/Power-Spectral_Density |
}} | }} | ||
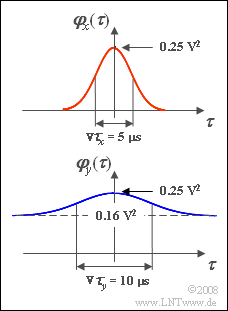
| − | [[File:P_ID411__Sto_A_4_13.png|right|frame| | + | [[File:P_ID411__Sto_A_4_13.png|right|frame|Two Gaussian ACF]] |
| − | + | Let the random process considered here $\{x_i(t)\}$ be characterized by the autocorrelation function (ACF) outlined above This random process is mean-free and the equivalent ACF duration is ${ {\rm \nabla} }\tau_x = 5 \hspace{0.08cm} \rm µ s$: | |
:$$\varphi_x(\tau)=\rm 0.25 V^2\cdot \rm e^{-\pi \hspace{0.03cm}\cdot \hspace{0.03cm} ({\tau}{/ 5 \hspace{0.08cm}{\rm µ}s })^2} .$$ | :$$\varphi_x(\tau)=\rm 0.25 V^2\cdot \rm e^{-\pi \hspace{0.03cm}\cdot \hspace{0.03cm} ({\tau}{/ 5 \hspace{0.08cm}{\rm µ}s })^2} .$$ | ||
| − | + | The bottom figure shows the ACF of the process $\{y_i(t)\}$ This reads with the equivalent ACF duration ${ {\rm \nabla} }\tau_y = 10 \hspace{0.08cm} \rm µ s$: | |
| − | |||
| − | |||
:$$ \varphi_y(\tau)=\rm 0.16 V^2 + \rm 0.09 V^2\cdot\rm e^{-\pi \hspace{0.03cm}\cdot \hspace{0.03cm} ({\tau}/{\nabla \it \tau_y})^2} .$$ | :$$ \varphi_y(\tau)=\rm 0.16 V^2 + \rm 0.09 V^2\cdot\rm e^{-\pi \hspace{0.03cm}\cdot \hspace{0.03cm} ({\tau}/{\nabla \it \tau_y})^2} .$$ | ||
| − | In | + | In this exercise, the Power spectral densities of the two processes are sought. |
| Line 21: | Line 19: | ||
| − | + | Hints: | |
| − | * | + | *This exercise belongs to the chapter [[Theory_of_Stochastic_Signals/Power-Spectral_Density|Power-Spectral Density]]. |
| − | * | + | *Reference is also made to the chapter [[Theory_of_Stochastic_Signals/Auto-Correlation_Function|Auto-correlation function]]. |
| − | * | + | *To solve this exercise you can use the following Fourier correspondence: |
| − | :$$\rm e^{-\pi \hspace{0.03cm}\cdot \hspace{0.03cm} ({\it f}/{\rm \Delta\it f})^2}\ \bullet\!\!- | + | :$$\rm e^{-\pi \hspace{0.03cm}\cdot \hspace{0.03cm} ({\it f}/{\rm \Delta\it f})^2}\ \bullet\!\!-\!\!-\!\!-\!-\!\!\circ\, \ {\rm \Delta \it f} \cdot \rm e^{-\pi \hspace{0.05cm}\cdot \hspace{0.05cm} ({\rm \Delta\it f} \hspace{0.05cm}\cdot \hspace{0.05cm}\it t {\rm )}^{\rm 2}}.$$ |
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {What is the äequivalent PSD bandwidth of the process $\{x_i(t)\}$? |
|type="{}"} | |type="{}"} | ||
| − | $ {\rm \nabla} \hspace{-0.05cm} f_x \ = \ $ { 200 3% } $\ | + | $ {\rm \nabla} \hspace{-0.05cm} f_x \ = \ $ { 200 3% } $\ \rm kHz$ |
| − | { | + | {What is ${\it \Phi}_x(f)$? Give the PSD values for $f= 0$ and $f = 200 \hspace{0.08cm} \rm kHz$ on. |
|type="{}"} | |type="{}"} | ||
| − | ${\it \Phi}_x(f = 0)\ = \ $ { 1.25 3% } | + | ${\it \Phi}_x(f = 0)\ = \ $ { 1.25 3% } $\ \cdot 10^{-6} \ \rm V^2\hspace{-0.1cm}/Hz$ |
| − | ${\it \Phi}_x(f = 200 \hspace{0.08cm} \rm kHz)\ = \ $ { 0.054 3% } | + | ${\it \Phi}_x(f = 200 \hspace{0.08cm} \rm kHz)\ = \ $ { 0.054 3% } $\ \cdot 10^{-6} \ \rm V^2\hspace{-0.1cm}/Hz$ |
| − | { | + | {Which statements are valid, if the random process has no periodic parts? Furthermore, a constant power is assumed. |
|type="[]"} | |type="[]"} | ||
| − | + | + | + The process power is the integral over the PSD. |
| − | + | + | + If the process is zero mean, the PSD is always continuous. |
| − | - | + | - The wider the ACF, the wider the PSD. |
| − | + | + | + A wider ACF results in higher PSD values. |
| − | + | {Calculate the Power spectral density spectrum ${\it \Phi}_y(f)$. What are the values for the continuous PSD component at $f= 0$ and $f = 200 \hspace{0.08cm} \rm kHz$? | |
| − | |||
| − | { | ||
|type="{}"} | |type="{}"} | ||
| − | ${\it \Phi}_y(f = 0)\ = | + | ${\it \Phi}_y(f = 0)\ = \ $ { 0.9 3% } $\ \cdot 10^{-6} \ \rm V^2\hspace{-0.1cm}/Hz$ |
| − | ${\it \Phi}_y(f = 200 \hspace{0.08cm} \rm kHz)\ = | + | ${\it \Phi}_y(f = 200 \hspace{0.08cm} \rm kHz)\ = \ $ { 0.0165 3% } $\ \cdot 10^{-6} \hspace{0.05cm} \rm V^2\hspace{-0.1cm}/Hz$ |
| − | { | + | {Which of the following statements are true regarding the process $\{y_i(t)\}$? |
|type="[]"} | |type="[]"} | ||
| − | - | + | - The PSD involves a Dirac at frequency $ f = {\rm \nabla} \hspace{-0.05cm} f_y$. |
| − | + | + | + The PSD involves a Dirac at frequency $f= 0$. |
| − | - | + | - Dirac weight and continuous PSD have the same unit. |
| − | |||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' The equivalent PSD bandwidth is the reciprocal of the equivalent ACF duration: |
:$$\nabla f_x = 1 / \nabla \tau_x \hspace{0.15cm}\underline{= {\rm 200\hspace{0.1cm}kHz}}.$$ | :$$\nabla f_x = 1 / \nabla \tau_x \hspace{0.15cm}\underline{= {\rm 200\hspace{0.1cm}kHz}}.$$ | ||
| − | '''(2)''' | + | '''(2)''' One can adapt the given Fourier correspondence to the task as follows: |
| − | :$$K\cdot{\rm e}^{-\pi({\tau}/{\nabla\tau_x})^2}\ \circ\!\!-\!\!\! | + | :$$K\cdot{\rm e}^{-\pi({\tau}/{\nabla\tau_x})^2}\ \circ\!\!-\!\!-\!\!-\!\!-\!-\!\bullet\,\ \frac{\it K}{\nabla \it f_x}\cdot{\rm e}^{-\pi({f}/{\nabla f_x})^2}.$$ |
| − | * | + | *With $K = 0.25 \hspace{0.05cm}\rm V^2$ and $ {\rm \nabla} \hspace{-0.05cm} f_x = 200\hspace{0.05cm} \rm kHz$ obtains: |
:$${\it \Phi_x}(f)=1.25\cdot\rm 10^{-\rm 6}\hspace{0.1cm}\frac{V^2}{Hz}\cdot\rm e^{-\pi({\it f}/{\nabla\it f_x})^2}\hspace{0.3cm} | :$${\it \Phi_x}(f)=1.25\cdot\rm 10^{-\rm 6}\hspace{0.1cm}\frac{V^2}{Hz}\cdot\rm e^{-\pi({\it f}/{\nabla\it f_x})^2}\hspace{0.3cm} | ||
\Rightarrow \hspace{0.3cm}{\it \Phi_x}(f = 0)=\hspace{0.15cm}\underline{\rm 1.25 \cdot 10^{-6} \hspace{0.1cm} V^2\hspace{-0.1cm}/Hz}, | \Rightarrow \hspace{0.3cm}{\it \Phi_x}(f = 0)=\hspace{0.15cm}\underline{\rm 1.25 \cdot 10^{-6} \hspace{0.1cm} V^2\hspace{-0.1cm}/Hz}, | ||
| Line 82: | Line 77: | ||
| − | '''(3)''' | + | '''(3)''' Correct <u>solutions 1, 2, and 4</u>: |
| − | * | + | *A mean-free process always results in a continuous PSD. This is narrower the wider the ACF is (reciprocitylaw). |
| − | * | + | *The process power is equal to the integral of the PSD. |
| − | * | + | *Therefore, at constant power, a wider ACF (narrower PSD) must be compensated by higher PSD values. |
| − | * | + | *A DC component or periodic components always result in dirac functions in the PSD; otherwise, the PSD is always continuous in value. |
| − | '''(4)''' | + | '''(4)''' Analogous to subtask '''(2)''' holds with $ {\rm \nabla} \hspace{-0.05cm} f_y = 100\hspace{0.05cm} \rm kHz$: |
:$${\it \Phi_y}(f)=\frac{\rm 0.09 V^2}{\nabla\it f_y}\cdot\rm e^{-\pi({\it f}/{\nabla\it f_y})^2}+\it m_y^{\rm 2}\cdot\delta(f).$$ | :$${\it \Phi_y}(f)=\frac{\rm 0.09 V^2}{\nabla\it f_y}\cdot\rm e^{-\pi({\it f}/{\nabla\it f_y})^2}+\it m_y^{\rm 2}\cdot\delta(f).$$ | ||
| − | * | + | *Because of the DC component, there is a Dirac at frequency $f = 0$ in addition to the continuous PSD component. |
| − | * | + | *The continuous PSD–part at $f= 0$ is ${\it \Phi_y}(f = 0)=\hspace{0.15cm}\underline{\rm 0.9 \cdot 10^{-6} \hspace{0.1cm} V^2\hspace{-0.1cm}/Hz}.$ |
| − | * | + | *The fraction at $f = 2 \cdot {\rm \nabla} \hspace{-0.05cm} f_y = 200 \hspace{0.05cm}\rm kHz$ is increased by a factor ${\rm e}^{-4} \approx 0.0183$ lower ⇒ ${\it \Phi_y}(f )=\hspace{0.15cm}\underline{\rm 0.0165 \cdot 10^{-6} \hspace{0.1cm} V^2\hspace{-0.1cm}/Hz}.$ |
| − | '''(5)''' | + | '''(5)''' Correct is <u>only the second proposed solution</u>: |
| − | * | + | *The PSD of a mean-valued process generally involves a Dirac function at $f=0$ with weight $m_y^2$. |
| − | * | + | *In the present case, this value is equal to $0.16 \ \rm V^2$. |
| − | * | + | *Since $\delta(f)$ has unit $\rm 1/Hz = s$ , the units of the continuous and discrete PSD components differ. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Revision as of 20:18, 7 March 2022
Let the random process considered here $\{x_i(t)\}$ be characterized by the autocorrelation function (ACF) outlined above This random process is mean-free and the equivalent ACF duration is ${ {\rm \nabla} }\tau_x = 5 \hspace{0.08cm} \rm µ s$:
- $$\varphi_x(\tau)=\rm 0.25 V^2\cdot \rm e^{-\pi \hspace{0.03cm}\cdot \hspace{0.03cm} ({\tau}{/ 5 \hspace{0.08cm}{\rm µ}s })^2} .$$
The bottom figure shows the ACF of the process $\{y_i(t)\}$ This reads with the equivalent ACF duration ${ {\rm \nabla} }\tau_y = 10 \hspace{0.08cm} \rm µ s$:
- $$ \varphi_y(\tau)=\rm 0.16 V^2 + \rm 0.09 V^2\cdot\rm e^{-\pi \hspace{0.03cm}\cdot \hspace{0.03cm} ({\tau}/{\nabla \it \tau_y})^2} .$$
In this exercise, the Power spectral densities of the two processes are sought.
Hints:
- This exercise belongs to the chapter Power-Spectral Density.
- Reference is also made to the chapter Auto-correlation function.
- To solve this exercise you can use the following Fourier correspondence:
- $$\rm e^{-\pi \hspace{0.03cm}\cdot \hspace{0.03cm} ({\it f}/{\rm \Delta\it f})^2}\ \bullet\!\!-\!\!-\!\!-\!-\!\!\circ\, \ {\rm \Delta \it f} \cdot \rm e^{-\pi \hspace{0.05cm}\cdot \hspace{0.05cm} ({\rm \Delta\it f} \hspace{0.05cm}\cdot \hspace{0.05cm}\it t {\rm )}^{\rm 2}}.$$
Questions
Solution
- $$\nabla f_x = 1 / \nabla \tau_x \hspace{0.15cm}\underline{= {\rm 200\hspace{0.1cm}kHz}}.$$
(2) One can adapt the given Fourier correspondence to the task as follows:
- $$K\cdot{\rm e}^{-\pi({\tau}/{\nabla\tau_x})^2}\ \circ\!\!-\!\!-\!\!-\!\!-\!-\!\bullet\,\ \frac{\it K}{\nabla \it f_x}\cdot{\rm e}^{-\pi({f}/{\nabla f_x})^2}.$$
- With $K = 0.25 \hspace{0.05cm}\rm V^2$ and $ {\rm \nabla} \hspace{-0.05cm} f_x = 200\hspace{0.05cm} \rm kHz$ obtains:
- $${\it \Phi_x}(f)=1.25\cdot\rm 10^{-\rm 6}\hspace{0.1cm}\frac{V^2}{Hz}\cdot\rm e^{-\pi({\it f}/{\nabla\it f_x})^2}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}{\it \Phi_x}(f = 0)=\hspace{0.15cm}\underline{\rm 1.25 \cdot 10^{-6} \hspace{0.1cm} V^2\hspace{-0.1cm}/Hz}, \hspace{0.5cm}{\it \Phi_x}(f = 200 \hspace{0.05cm} \rm kHz)=\hspace{0.15cm}\underline{\rm 0.054 \cdot 10^{-6} \hspace{0.1cm} V^2\hspace{-0.1cm}/Hz}.$$
(3) Correct solutions 1, 2, and 4:
- A mean-free process always results in a continuous PSD. This is narrower the wider the ACF is (reciprocitylaw).
- The process power is equal to the integral of the PSD.
- Therefore, at constant power, a wider ACF (narrower PSD) must be compensated by higher PSD values.
- A DC component or periodic components always result in dirac functions in the PSD; otherwise, the PSD is always continuous in value.
(4) Analogous to subtask (2) holds with $ {\rm \nabla} \hspace{-0.05cm} f_y = 100\hspace{0.05cm} \rm kHz$:
- $${\it \Phi_y}(f)=\frac{\rm 0.09 V^2}{\nabla\it f_y}\cdot\rm e^{-\pi({\it f}/{\nabla\it f_y})^2}+\it m_y^{\rm 2}\cdot\delta(f).$$
- Because of the DC component, there is a Dirac at frequency $f = 0$ in addition to the continuous PSD component.
- The continuous PSD–part at $f= 0$ is ${\it \Phi_y}(f = 0)=\hspace{0.15cm}\underline{\rm 0.9 \cdot 10^{-6} \hspace{0.1cm} V^2\hspace{-0.1cm}/Hz}.$
- The fraction at $f = 2 \cdot {\rm \nabla} \hspace{-0.05cm} f_y = 200 \hspace{0.05cm}\rm kHz$ is increased by a factor ${\rm e}^{-4} \approx 0.0183$ lower ⇒ ${\it \Phi_y}(f )=\hspace{0.15cm}\underline{\rm 0.0165 \cdot 10^{-6} \hspace{0.1cm} V^2\hspace{-0.1cm}/Hz}.$
(5) Correct is only the second proposed solution:
- The PSD of a mean-valued process generally involves a Dirac function at $f=0$ with weight $m_y^2$.
- In the present case, this value is equal to $0.16 \ \rm V^2$.
- Since $\delta(f)$ has unit $\rm 1/Hz = s$ , the units of the continuous and discrete PSD components differ.