Aufgaben:Exercise 3.9: Circular Arc and Parabola

• Return to book

Locus curves in FM:
Arc and Parabola

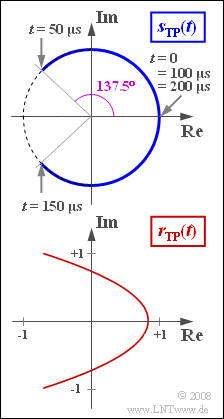
We now consider the frequency modulation of a cosine source signal

$$q(t) = A_{\rm N} \cdot \cos(2 \pi \cdot f_{\rm N} \cdot t )$$

with amplitude  $A_{\rm N} = 1 \ \rm V$  and frequency $f_{\rm N} = 5 \ \rm kHz$.

• The modulation index (phase deviation) is  $η = 2.4$.
• The corresponding low-pass signal with normalized carrier amplitude  $(A_{\rm T} = 1)$ is:

$$ s_{\rm TP}(t) = \sum_{n = - \infty}^{+\infty}{\rm J}_n (\eta) \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}n\hspace{0.05cm}\cdot \hspace{0.05cm}\omega_{\rm N} \hspace{0.05cm}\cdot \hspace{0.05cm} t}.$$

• This represents an arc.  Within the period $T_{\rm N} = 1/f_{\rm N} = 200 \ \rm µ s$  the following phase angles result:

$$ \phi(0) = 0, \hspace{0.2cm}\phi(0.25 \cdot T_{\rm N}) = \eta, \hspace{0.2cm}\phi(0.5 \cdot T_{\rm N})= 0,\hspace{0.2cm} \phi(0.75 \cdot T_{\rm N})= -\eta,\hspace{0.2cm}\phi(T_{\rm N})= 0.$$

• Theoretically, the channel bandwidth required to transmit this signal is infinite.

However, if the bandwidth is limited to  $B_{\rm K} = 25 \ \rm kHz$, for example,the equivalent low-pass signal of the received signal can be described as follows:

$$r_{\rm TP}(t) = \sum_{n = - 2}^{+2}{\rm J}_n (\eta) \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}n\hspace{0.05cm}\cdot \hspace{0.05cm}\omega_{\rm N} \hspace{0.05cm}\cdot \hspace{0.05cm} t}.$$

In this case, the result is a parabolic locus curve

$$ y^2 + a \cdot x + b = 0,$$

which will be analyzed in this task.

Hints:

• This exercise belongs to the chapter  Frequency Modulation.
• Reference is also made to the chapter  Phase Modulation  and particularly to the section  Signal characteristics with frequency modulation.
• During calculation, assume the following values of the Bessel function:

$${\rm J}_0 (2.4) \approx 0, \hspace{0.2cm}{\rm J}_1 (2.4) = -{\rm J}_{-1} (2.4)\approx 0.52, \hspace{0.2cm}{\rm J}_2 (2.4) = {\rm J}_{-2} (2.4)\approx 0.43.$$

Question

1

What is the modulator constant  $K_{\rm FM}$?

$K_{\rm FM} \ = \ $ $\ \cdot 10^4 \ \rm (Vs)^{-1}$

2

Calculate the real part $x(t) = {\rm Re}\big[r_{\rm TP}(t)\big]$  of the equivalent low-pass signal and give its maximum and minimum.

$x_{\rm max} \ = \ $

$x_{\rm min} \ = \ $

3

What is the maximum and minimum of the imaginary part  $y(t) = {\rm Im}\big[r_{\rm TP}(t)\big]$?

$y_{\rm max} \ = \ $

$y_{\rm min} \ = \ $

4

What are the phase values for all multiples of  $T_{\rm N}/2$?

$ϕ(t = n · T_{\rm N}/2) \ = \ $ $\ \rm degrees$

5

What is the maximum phase angle  $ϕ_{\rm max}$?  Interpret the result.

$ϕ_{\rm max} \ = \ $ $\ \rm degrees$

6

Show that the locus curve can be given in the form  $y^2 + a · x + b = 0$ .  Determine the parabolic parameters  $a$  and  $b$.

$a\ = \ $

$b\ = \ $

Solution

Solution

(1)  In the frequency modulation of a cosine signal, the modulation index is:

$$ \eta = \frac{K_{\rm FM} \cdot A_{\rm N}}{ \omega_{\rm N}} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} K_{\rm FM} = \frac{2 \pi \cdot f_{\rm N }\cdot \eta}{ A_{\rm N}} = \frac{2 \pi \cdot 5 \cdot 10^3 \,{\rm Hz}\cdot 2.4}{ 1\,{\rm V}} \hspace{0.15cm}\underline {\approx 7.54 }\cdot 10^4 \,\,{\rm V}^{-1}{\rm s}^{-1}\hspace{0.05cm}.$$

(2)  The equation given for the equivalent low-pass signal when  $γ = ω_{\rm N} · t$  and considering   ${\rm J}_{–1} = –{\rm J}_1$  and  ${\rm J}_{–2} = {\rm J}_2$, is written out as:

$$r_{\rm TP}(t) = {\rm J}_0 + \left[ {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} \gamma} - {\rm e}^{\hspace{0.05cm}{-\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} \gamma} \right]\cdot {\rm J}_1 \hspace{0.27cm} +\left[ {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2\gamma} + {\rm e}^{\hspace{0.05cm}{-\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2\gamma} \right]\cdot {\rm J}_2 = {\rm J}_0 + 2 \cdot {\rm j} \cdot {\rm J}_1 \cdot \sin (\gamma)+ 2 \cdot {\rm J}_2 \cdot \cos (2\gamma)\hspace{0.05cm} .$$

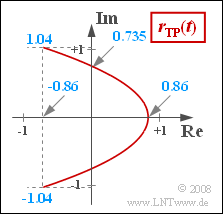
• Thus, for the real part in general, including for   $η = 2.4$, that is,  ${\rm J}_0 = 0$  and  ${\rm J}_2 = 0.43$:

$$ x(t) = {\rm J}_0 + 2 \cdot {\rm J}_2 \cdot \cos (2 \omega_{\rm N} t ) = 2 \cdot {\rm J}_2 \cdot \cos (2 \omega_{\rm N} t ) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} x_{\rm max} = 2 \cdot {\rm J}_2\hspace{0.15cm}\underline { = 0.86}, \hspace{0.3cm} x_{\rm min} = -x_{\rm max} \hspace{0.15cm}\underline {= -0.86}\hspace{0.05cm}.$$

(3)  According to the result of question  (2)  we get an imginary part   $({\rm J}_1 = 0.52)$ of:

$$y(t) = 2 \cdot {\rm J}_1 \cdot \sin ( \omega_{\rm N} t )\hspace{0.3cm}\Rightarrow \hspace{0.3cm} y_{\rm max} =2 \cdot {\rm J}_1\hspace{0.15cm}\underline { = 1.04}\hspace{0.05cm}, \hspace{0.3cm} y_{\rm min} = -y_{\rm max}\hspace{0.15cm}\underline { = -1.04}\hspace{0.05cm}.$$

(4)  The imaginary part is zero at each of these time points and so is the phase function:

$$ϕ(t = n · T_{\rm N}/2)\hspace{0.15cm}\underline{= 0}.$$

• This fact can also be seen from the sketch on the exercise page.

(5)  From the sketch it can already be seen that the phase angle reaches its maximum value at  $t = T_{\rm N}/4$ , for example.

• This can be calculated with  $y_{\rm max} = 1.04$  and  $x_{\rm min} = -0.86$  as follows:

$$\phi_{\rm max} = \arctan \frac{y_{\rm max}}{x_{\rm min}} = \arctan (-1.21) = 180^\circ - 50.4^\circ \hspace{0.15cm}\underline {= 129.6^\circ} \hspace{0.05cm}.$$

• Without band-limiting, the phase angle here would be $ϕ(t = T_{\rm N}/4) = η = 2.4 = 137.5^\circ$ .
• Thus, the maximum deviation of the sink signal from the source signal occurs at time  $t = T_{\rm N}/4$ , for example.

Parabolic progression

(6)  Using  $γ = ω_{\rm N} · t$  and  $\cos(2γ) = 1 - 2 · \cos^2(γ)$  the real and imaginary parts can be written as:

$$x = {\rm J}_0 + 4 \cdot {\rm J}_2 \cdot \cos^2 (\gamma) - 2 \cdot {\rm J}_2\hspace{0.05cm},\hspace{0.3cm} y = 2 \cdot {\rm J}_1 \cdot \sin (\gamma) \hspace{0.05cm}.$$

• These equations can be rearranegd:

$$\cos^2 (\gamma) =\frac{x-{\rm J}_0 + 2 \cdot {\rm J}_2 }{4 \cdot {\rm J}_2} \hspace{0.05cm},\hspace{0.3cm} \sin^2 (\gamma) = \frac{y^2 }{4 \cdot {\rm J}_1^2}$$

$$\Rightarrow \hspace{0.3cm} \frac{y^2 }{4 \cdot {\rm J}_1^2} + \frac{x-{\rm J}_0 + 2 \cdot {\rm J}_2 }{4 \cdot {\rm J}_2} =1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} {y^2 } + \frac{{\rm J}_1^2}{ {\rm J}_2} \cdot x + {{\rm J}_1^2} \cdot \left ( 2 - \frac{{\rm J}_0}{ {\rm J}_2} \right ) =0\hspace{0.05cm}.$$

• Thus, the parabolic parameters for  $ {\rm J}_0 = 0$ are:

$$a = \frac{{\rm J}_1^2}{ {\rm J}_2} \hspace{0.15cm}\underline {\approx 0.629}, \hspace{0.3cm} b = 2 \cdot {\rm J}_1^2 \hspace{0.15cm}\underline {\approx 0.541} \hspace{0.05cm}.$$

• To double-check, we use   $y = 0$   ⇒   $ x_{\rm max} = {b}/{a} = 2 \cdot {\rm J}_2 = 0.86 \hspace{0.05cm}.$
• Thus, the values at  $x = 0$  are     $y_0 = \pm \sqrt{2} \cdot {\rm J}_1 \approx 0.735 \hspace{0.05cm}.$