Aufgaben:Exercise 4.10Z: Correlation Duration

• Return to book

Sample functions of ergodic processes

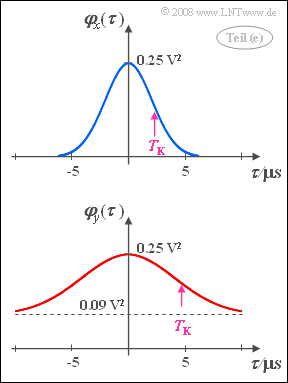
The graphic shows pattern signals of two random processes  $\{x_i(t)\}$  and  $\{y_i(t)\}$  with equal power 

$$P_x = P_y = 5\hspace{0.05 cm} \rm mW.$$

Assuming here the resistance  $R = 50\hspace{0.05 cm}\rm \Omega$.

The random process  $\{x_i(t)\}$

• is zero mean  $(m_x = 0)$,
• has the Gaussian ACF   $\varphi_x (\tau) = \varphi_x (\tau = 0) \cdot {\rm e}^{- \pi \hspace{0.03cm} \cdot \hspace{0.03cm}(\tau / {\rm \nabla} \tau_x)^2},$  and
• exhibits the equivalent ACF duration  $\nabla \tau_x = 5\hspace{0.05 cm}\rm µ s $ .

As can be seen from the diagram below,  the random process  $\{y_i(t)\}$  has much stronger internal statistical bindings than the random process  $\{x_i(t)\}$. Or,  to put it another way:

• The random process  $\{y_i(t)\}$  is lower frequency than  $\{x_i(t)\}$.
• The equivalent ACF duration is  $\nabla \tau_y = 10 \hspace{0.05 cm}\rm µ s $.

From the sketch it can also be seen that  $\{y_i(t)\}$  in contrast to  $\{x_i(t)\}$  is not DC free.  The DC signal component is rather  $m_y = -0.3 \hspace{0.05 cm}\rm V$.

Hint:

• The exercise belongs to the chapter  Auto-Correlation Function.
• Reference is made in particular to the section  Interpretation of the auto-correlation function.

Questions

1

What is the standard deviation  $(\sigma_x)$  of the pattern signals of the process  $\{x_i(t)\}$?

$\sigma_x \ = \ $ $\ \rm V$

2

What ACF values result for  $\tau = 2\hspace{0.05 cm}\rm µs$  resp.  $\tau = 5\hspace{0.05 cm}\rm µ s$?

$\varphi_x(\tau = 2\hspace{0.05 cm}{\rm µ s}) \ = \ $ $\ \rm mW$

$\varphi_x(\tau = 5\hspace{0.05 cm}{\rm µ s}) \ = \ $ $\ \rm mW$

3

What is the correlation time  $T_{\rm K}$,  i.e. the time at which the ACF has dropped to half of the maximum?

$T_{\rm K} \ = \ $ $\ \rm µ s$

4

What is the standard deviation  $(\sigma_y)$  of the pattern signals of the process $\{y_i(t)\}$?

$\sigma_y \ = \ $ $\ \rm V$

5

Calculate the ACF  $\varphi_x(\tau)$.  What is the ACF value at  $\tau = 10\hspace{0.05 cm}\rm µ s$?  What would be the ACF curve with positive mean  $(m_y = +0.3 \hspace{0.05 cm}\rm V)$?

$\varphi_y(\tau = 10\hspace{0.05 cm}{\rm µ s}) \ = \ $ $\ \rm mW$

Solution

Solution

(1)  The quadratic mean results to  $m_{2x} = R \cdot P_x = 50 \hspace{0.05 cm}{\rm \Omega}\cdot 5 \hspace{0.05 cm}{\rm mW}= 0.25 \hspace{0.05 cm}{\rm V}^2.$

• From this follows the standard deviation  $\sigma_x\hspace{0.15 cm}\underline{= 0.5\hspace{0.05 cm}{\rm V}}$.

(2)  Because  $P_x = \varphi_x (\tau = 0)$  holds for the ACF in general:

$$\varphi_x (\tau) = 5 \hspace{0.1cm} {\rm mW} \cdot {\rm e}^{- \pi \hspace{0.03cm} \cdot \hspace{0.03cm}(\tau / {\rm \nabla} \tau_x)^2}.$$

• From this we obtain:

$$\varphi_x (\tau = {\rm 2\hspace{0.1cm} µ s}) = 5 \hspace{0.1cm} {\rm mW} \cdot {\rm e}^{- {\rm 0.16 }\pi } \hspace{0.15cm}\underline{= 3.025 \hspace{0.1cm} \rm mW},$$

$$\varphi_x (\tau = {\rm 5\hspace{0.1cm} \rm µ s}) = 5 \hspace{0.1cm} {\rm mW} \cdot {\rm e}^{- \pi } \hspace{0.15cm}\underline{= 0.216 \hspace{0.1cm} \rm mW}.$$

Two times Gaussian ACF

(3)  Here the following determination equation holds:

$${\rm e}^{- \pi \hspace{0.03cm} \cdot \hspace{0.03cm}(T_{\rm K} / {\rm \nabla} \tau_x)^2} \stackrel{!}{=} {\rm 0.5} \hspace{0.5cm}\Rightarrow\hspace{0.5cm} (T_{\rm K} / {\rm \nabla} \tau_x)^2 = \sqrt{{ \ln(2)}/{\pi}}\hspace{0.05cm}.$$

• From this follows  $T_{\rm K}\hspace{0.15 cm}\underline{= 2.35\hspace{0.05 cm}{\rm µ s}}$.
• With other ACF form, a different ratio is obtained for  $T_{\rm K} / {\rm \nabla} \tau_x$.

(4)  Because  $P_x = P_y$  the root mean square values of  $x$  and  $y$  are equal, respectively  $0.25\hspace{0.05 cm}\rm V^2$.

• Taking into account the mean value  $m_y = -0.3 \hspace{0.05 cm}\rm V$  holds:

$$m_y^2 + \sigma_y^2 = \rm 0.25 \hspace{0.05 cm} V^2.$$

• From this follows:

$$\sigma_y\hspace{0.15 cm}\underline{= 0.4\hspace{0.05 cm}{\rm V}}.$$

(5)  In terms of unit resistance  $ R = 1 \hspace{0.05 cm}{\rm \Omega}$  the ASF of the process  $\{y_i(t)\}$ is:

$$\varphi_y (\tau) = m_y^2 + \sigma_y^2 \cdot {\rm e}^{- \pi \hspace{0.03cm} \cdot \hspace{0.03cm}(\tau / {\rm \nabla} \tau_y)^2}.$$

• On the right you can see the function progression.  Related to the resistor  $ R = 50 \hspace{0.05 cm}{\rm \Omega}$  results in the following ACF values:

$$\varphi_y (\tau = 0) = 5 \hspace{0.1cm} {\rm mW} , \hspace{0.5cm} \varphi_y (\tau \rightarrow \infty) = 1.8\hspace{0.1cm} {\rm mW} .$$

• From this follows:

$$\varphi_y(\tau) = 1.8 \hspace{0.1cm} {\rm mW} + 3.2 \hspace{0.1cm} {\rm mW} \cdot {\rm e}^{- \pi \hspace{0.03cm} \cdot \hspace{0.03cm}(\tau / {\rm \nabla} \tau_y)^2} \hspace{0.3cm }\Rightarrow \hspace{0.3cm }\varphi_y(\tau = 10\hspace{0.05 cm}{\rm µ s}) \hspace{0.15 cm}\underline{=1.938\hspace{0.05 cm}\rm mW}.$$

• With positive mean  $m_y$  (having the same amplitude), there would be no change in the ASF, since  $m_y$  is squared in the ASF equation.