Difference between revisions of "Aufgaben:Exercise 1.08: Comparison of ASK and BPSK"
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Digital_Signal_Transmission/Linear_Digital_Modulation_-_Coherent_Demodulation |
}} | }} | ||
| − | [[File:P_ID1680__Dig_A_4_1.png|right|frame| | + | [[File:P_ID1680__Dig_A_4_1.png|right|frame|Bit error probabilities <br>of ASK and BPSK]] |
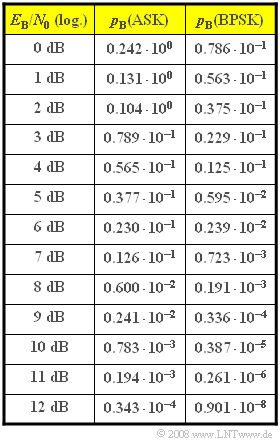
| − | + | The bit error probabilities of ''Amplitude Shift Keying'' (ASK) and ''Binary Shift Keying'' (BPSK) modulation modes are often given by the following two equations: | |
:$$p_{\rm ASK} = \ {\rm Q}\left ( \sqrt{\frac{E_{\rm B}}{N_0 }} \hspace{0.1cm}\right ) = \ {1}/{2}\cdot {\rm erfc}\left ( \sqrt{\frac{E_{\rm B}}{2 \cdot N_0 }} \right ),$$ | :$$p_{\rm ASK} = \ {\rm Q}\left ( \sqrt{\frac{E_{\rm B}}{N_0 }} \hspace{0.1cm}\right ) = \ {1}/{2}\cdot {\rm erfc}\left ( \sqrt{\frac{E_{\rm B}}{2 \cdot N_0 }} \right ),$$ | ||
:$$ p_{\rm BPSK} = \ {\rm Q}\left ( \sqrt{\frac{2 \cdot E_{\rm B}}{N_0 }} \hspace{0.1cm}\right ) = \ {1}/{2}\cdot {\rm erfc}\left ( \sqrt{\frac{E_{\rm B}}{ N_0 }} \right ).$$ | :$$ p_{\rm BPSK} = \ {\rm Q}\left ( \sqrt{\frac{2 \cdot E_{\rm B}}{N_0 }} \hspace{0.1cm}\right ) = \ {1}/{2}\cdot {\rm erfc}\left ( \sqrt{\frac{E_{\rm B}}{ N_0 }} \right ).$$ | ||
| − | + | These two equations are evaluated in the attached table. The following applies: | |
| − | *$E_{\rm B}$ | + | *$E_{\rm B}$ indicates the average energy per bit. |
| − | *$N_{0}$ | + | *$N_{0}$ is the noise power density. |
| − | * | + | *There is a fixed relationship between the error functions ${\rm Q}(x)$ and ${\rm erfc}(x)$. |
| − | + | It should be noted that these equations do not apply in general, but only under certain idealized conditions. These conditions are to be worked out in this exercise. | |
| Line 21: | Line 21: | ||
| − | '' | + | ''Notes:'' |
| − | * | + | *The exercise belongs to the chapter [[Digital_Signal_Transmission/Linear_Digital_Modulation_-_Coherent_Demodulation|Linear Digital Modulation - Coherent Demodulation]]. |
| − | * | + | *You can check the results with the applet [[Applets:Komplementäre_Gaußsche_Fehlerfunktionen|Complementary Gaussian Error Functions]]. |
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {What is the relationship between ${\rm Q}(x)$ and ${\rm erfc}(x)$? |
|type="[]"} | |type="[]"} | ||
| − | - | + | - ${\rm Q}(x)= 2 \cdot{\rm erfc}(x)$ holds, |
| − | + | + | + ${\rm Q}(x)= 0.5 \cdot{\rm erfc}(x)/\sqrt{2})$ holds, |
| − | - | + | - ${\rm erfc}(x)= 0.5 \cdot{\rm Q}(x)/\sqrt{2})$ holds. |
| − | { | + | {When do the given equations for the error probability apply? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + They apply only to the AWGN channel. |
| − | + | + | + They apply only to the matched filter receiver (or variants). |
| − | - | + | - The equations take into account intersymbol interfering. |
| − | - | + | - The equations apply only to rectangular signals. |
| − | { | + | {What are the error probabilities for $10 \cdot \lg \ E_{\rm B}/N_{0} = 12\, \rm dB$? |
|type="{}"} | |type="{}"} | ||
$ p_{\rm ASK} \ = \ $ { 0.343 3% } $\ \cdot 10^{-4}$ | $ p_{\rm ASK} \ = \ $ { 0.343 3% } $\ \cdot 10^{-4}$ | ||
$ p_{\rm BPSK} \ = \ $ { 0.901 3% } $\ \cdot 10^{-8}$ | $ p_{\rm BPSK} \ = \ $ { 0.901 3% } $\ \cdot 10^{-8}$ | ||
| − | { | + | {What are the error probabilities for $E_{\rm B}/N_{0} = 8$? |
|type="{}"} | |type="{}"} | ||
$ p_{\rm ASK} \ = \ $ { 0.241 3% } $\ \cdot 10^{-2}$ | $ p_{\rm ASK} \ = \ $ { 0.241 3% } $\ \cdot 10^{-2}$ | ||
$ p_{\rm BPSK} \ = \ $ { 0.336 3% } $\ \cdot 10^{-4}$ | $ p_{\rm BPSK} \ = \ $ { 0.336 3% } $\ \cdot 10^{-4}$ | ||
| − | { | + | {The error probability should not exceed $10^{-8}$. What is the required $10 \cdot \lg \ E_{\rm B}/N_{0}$ for ASK? |
|type="{}"} | |type="{}"} | ||
$(E_{\rm B}/N_{0})_{\rm min} \ = \ $ { 15 3% } $\ \rm dB $ | $(E_{\rm B}/N_{0})_{\rm min} \ = \ $ { 15 3% } $\ \rm dB $ | ||
| Line 63: | Line 63: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' It is already obvious from the equations on the information page that <u>solution 2</u> is correct. The defining equations are: |
:$$\rm Q ({\it x}) = \ \frac{\rm 1}{\sqrt{\rm 2\pi}}\int_{\it | :$$\rm Q ({\it x}) = \ \frac{\rm 1}{\sqrt{\rm 2\pi}}\int_{\it | ||
x}^{+\infty}\rm e^{\it -u^{\rm 2}/\rm 2}\,d \it u | x}^{+\infty}\rm e^{\it -u^{\rm 2}/\rm 2}\,d \it u | ||
| Line 72: | Line 72: | ||
\pi}}\int_{\it x}^{+\infty}\rm e^{\it -u^{\rm 2}}\,d \it u | \pi}}\int_{\it x}^{+\infty}\rm e^{\it -u^{\rm 2}}\,d \it u | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | By simple substitutions, the above relationship can be easily proved: | |
:$${\rm Q} ( x) = 1/2 \cdot {\rm erfc} (x/\sqrt{2}) \hspace{0.05cm}.$$ | :$${\rm Q} ( x) = 1/2 \cdot {\rm erfc} (x/\sqrt{2}) \hspace{0.05cm}.$$ | ||
| − | '''(2)''' | + | '''(2)''' The <u>first two solutions</u> are correct: |
| − | * | + | *The equations are valid only for the AWGN channel and for an optimal binary receiver, for example, according to the matched filter approach. |
| − | * | + | *Intersymbol interfering – caused by the channel or the receiver filter – is not covered by this. |
| − | * | + | *The exact transmission pulse shaping, on the other hand, does not matter as long as the receiver filter $H_{\rm E}(f)$ is matched to the transmission spectrum. Rather: |
| − | * | + | *Two different transmission pulse shapers $H_{\rm S}(f)$ lead to exactly the same error probability if they have the same energy per bit. |
| − | '''(3)''' | + | '''(3)''' The results can be read directly from the table: |
:$$p_{\rm ASK} \hspace{0.1cm}\underline {= 0.343 \cdot 10^{-4}},\hspace{0.3cm}p_{\rm BPSK} \hspace{0.1cm}\underline {= 0.901 \cdot 10^{-8}}.$$ | :$$p_{\rm ASK} \hspace{0.1cm}\underline {= 0.343 \cdot 10^{-4}},\hspace{0.3cm}p_{\rm BPSK} \hspace{0.1cm}\underline {= 0.901 \cdot 10^{-8}}.$$ | ||
| − | '''(4)''' | + | '''(4)''' With $E_{\rm B}/N_{0} = 8\ \Rightarrow \ 10 \cdot \lg \ E_{\rm B}/N_{0} \approx 9 \ \rm dB$, the following error probabilities are obtained: |
:$$p_{\rm ASK} \hspace{0.1cm}\underline {= 0.241 \cdot 10^{-2}},\hspace{0.3cm}p_{\rm BPSK} \hspace{0.1cm}\underline {= 0.336 \cdot 10^{-4}}.$$ | :$$p_{\rm ASK} \hspace{0.1cm}\underline {= 0.241 \cdot 10^{-2}},\hspace{0.3cm}p_{\rm BPSK} \hspace{0.1cm}\underline {= 0.336 \cdot 10^{-4}}.$$ | ||
| − | '''(5)''' | + | '''(5)''' From question '''(3)''', it follows that for binary phase modulation, $10 \cdot \lg \ E_{\rm B}/N_{0} \approx 12 \ \rm dB$ must be satisfied for $p_{\rm BPSK} \approx 10^{-8}$ to be possible. |
| − | * | + | *However, the given equations also show that the ASK curve is $3 \ \rm dB$ $($exactly $3.01 \ \rm dB)$ to the right of the BPSK curve. |
| − | * | + | *It follows that: |
:$$10 \cdot {\rm lg}\hspace{0.1cm}(E_{\rm B}/N_{\rm 0})_{\rm min}\hspace{0.1cm}\underline {\approx 15\,\,{\rm dB}} \hspace{0.05cm}.$$ | :$$10 \cdot {\rm lg}\hspace{0.1cm}(E_{\rm B}/N_{\rm 0})_{\rm min}\hspace{0.1cm}\underline {\approx 15\,\,{\rm dB}} \hspace{0.05cm}.$$ | ||
Revision as of 14:22, 29 March 2022
The bit error probabilities of Amplitude Shift Keying (ASK) and Binary Shift Keying (BPSK) modulation modes are often given by the following two equations:
- $$p_{\rm ASK} = \ {\rm Q}\left ( \sqrt{\frac{E_{\rm B}}{N_0 }} \hspace{0.1cm}\right ) = \ {1}/{2}\cdot {\rm erfc}\left ( \sqrt{\frac{E_{\rm B}}{2 \cdot N_0 }} \right ),$$
- $$ p_{\rm BPSK} = \ {\rm Q}\left ( \sqrt{\frac{2 \cdot E_{\rm B}}{N_0 }} \hspace{0.1cm}\right ) = \ {1}/{2}\cdot {\rm erfc}\left ( \sqrt{\frac{E_{\rm B}}{ N_0 }} \right ).$$
These two equations are evaluated in the attached table. The following applies:
- $E_{\rm B}$ indicates the average energy per bit.
- $N_{0}$ is the noise power density.
- There is a fixed relationship between the error functions ${\rm Q}(x)$ and ${\rm erfc}(x)$.
It should be noted that these equations do not apply in general, but only under certain idealized conditions. These conditions are to be worked out in this exercise.
Notes:
- The exercise belongs to the chapter Linear Digital Modulation - Coherent Demodulation.
- You can check the results with the applet Complementary Gaussian Error Functions.
Questions
Solution
- $$\rm Q ({\it x}) = \ \frac{\rm 1}{\sqrt{\rm 2\pi}}\int_{\it x}^{+\infty}\rm e^{\it -u^{\rm 2}/\rm 2}\,d \it u \hspace{0.05cm},$$
- $$\rm erfc ({\it x}) = \ \frac{\rm 2}{\sqrt{\rm \pi}}\int_{\it x}^{+\infty}\rm e^{\it -u^{\rm 2}}\,d \it u \hspace{0.05cm}.$$
By simple substitutions, the above relationship can be easily proved:
- $${\rm Q} ( x) = 1/2 \cdot {\rm erfc} (x/\sqrt{2}) \hspace{0.05cm}.$$
(2) The first two solutions are correct:
- The equations are valid only for the AWGN channel and for an optimal binary receiver, for example, according to the matched filter approach.
- Intersymbol interfering – caused by the channel or the receiver filter – is not covered by this.
- The exact transmission pulse shaping, on the other hand, does not matter as long as the receiver filter $H_{\rm E}(f)$ is matched to the transmission spectrum. Rather:
- Two different transmission pulse shapers $H_{\rm S}(f)$ lead to exactly the same error probability if they have the same energy per bit.
(3) The results can be read directly from the table:
- $$p_{\rm ASK} \hspace{0.1cm}\underline {= 0.343 \cdot 10^{-4}},\hspace{0.3cm}p_{\rm BPSK} \hspace{0.1cm}\underline {= 0.901 \cdot 10^{-8}}.$$
(4) With $E_{\rm B}/N_{0} = 8\ \Rightarrow \ 10 \cdot \lg \ E_{\rm B}/N_{0} \approx 9 \ \rm dB$, the following error probabilities are obtained:
- $$p_{\rm ASK} \hspace{0.1cm}\underline {= 0.241 \cdot 10^{-2}},\hspace{0.3cm}p_{\rm BPSK} \hspace{0.1cm}\underline {= 0.336 \cdot 10^{-4}}.$$
(5) From question (3), it follows that for binary phase modulation, $10 \cdot \lg \ E_{\rm B}/N_{0} \approx 12 \ \rm dB$ must be satisfied for $p_{\rm BPSK} \approx 10^{-8}$ to be possible.
- However, the given equations also show that the ASK curve is $3 \ \rm dB$ $($exactly $3.01 \ \rm dB)$ to the right of the BPSK curve.
- It follows that:
- $$10 \cdot {\rm lg}\hspace{0.1cm}(E_{\rm B}/N_{\rm 0})_{\rm min}\hspace{0.1cm}\underline {\approx 15\,\,{\rm dB}} \hspace{0.05cm}.$$