Difference between revisions of "Aufgaben:Exercise 4.4: About the Quantization Noise"
| Line 39: | Line 39: | ||
$P_{\rm S} \ = \ $ { 12 3% } $\ \rm V^2$ | $P_{\rm S} \ = \ $ { 12 3% } $\ \rm V^2$ | ||
| − | {Which statements are true for the error signal $ε(t)$ ? | + | {Which statements are true for the error signal $ε(t)= q_{\rm Q}(t)-q(t)$ ? |
|type="[]"} | |type="[]"} | ||
+ $ε(t)$ has a sawtooth shape. | + $ε(t)$ has a sawtooth shape. | ||
Revision as of 12:55, 9 April 2022
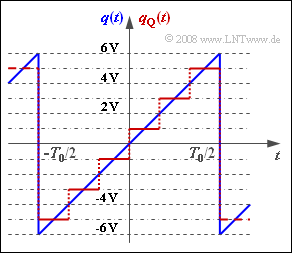
To calculate the quantization noise power $P_{\rm Q}$ we assume a periodic sawtooth-shaped source signal $q(t)$ with value range $±q_{\rm max}$ and period duration $T_0$ .
- In the mean time domain $-T_0/2 ≤ t ≤ T_0/2$ holds: $q(t) = q_{\rm max} \cdot \left ( {2 \cdot t}/{T_0} \right ).$
- We refer to the power of the signal $q(t)$ here as the transmit power $P_{\rm S}$.
The signal $q(t)$ is quantized according to the graph with $M = 6$ steps. The quantized signal is $q_{\rm Q}(t)$, where:
- The linear quantizer is designed for the amplitude range $±Q_{\rm max}$ such that each quantization interval has width ${\it Δ} = 2/M \cdot Q_{\rm max}$.
- The diagram shows this fact for $Q_{\rm max} = q_{\rm max} = 6 \ \rm V$. These numerical values shall be assumed up to and including the subtask (5).
The "quantization noise power" is defined as the second moment of the difference signal $ε(t) = q_{\rm Q}(t) - q(t)$. It holds:
- $$P_{\rm Q} = \frac{1}{T_0' } \cdot \int_{0}^{T_0'}\varepsilon(t)^2 \hspace{0.05cm}{\rm d}t \hspace{0.05cm},$$
where the time $T_0'$ is to be chosen appropriately. The "quantization SNR" is the ratio $\rho_{\rm Q} = {P_{\rm S}}/{P_{\rm Q}}\hspace{0.05cm}$, which is usually given logarithmically (in dB).
Hints:
- The exercise belongs to the chapter "Pulse Code Modulation".
- Reference is made in particular to the page "Quantization and quantization Noise".
Questions
Solution
- Due to periodicity and symmetry, averaging over the time domain $T_0/2$ is sufficient:
- $$P_{\rm S} = \frac{1}{T_0/2} \cdot \int_{0}^{T_0/2}q^2(t) \hspace{0.05cm}{\rm d}t = \frac{2 \cdot q_{\rm max}^2}{T_0} \cdot \int_{0}^{T_0/2}\left ( { 2 \cdot t}/{T_0} \right )^2 \hspace{0.05cm}{\rm d}t= \frac{2 \cdot q_{\rm max}^2}{T_0} \cdot \frac{T_0}{2} \cdot \int_{0}^{1}x^2 \hspace{0.05cm}{\rm d}x = \frac{q_{\rm max}^2}{3} \hspace{0.05cm}.$$
- Here the substitution $x = 2 - t/T_0$ was used. With $q_{\rm max} = 6 \ \rm V$ one gets $P_\rm S\hspace{0.15cm}\underline { = 12 \ V^2}$.
(2) Correct are suggested solutions 1, 3, and 4:
- We assume here $Q_{\rm max} = q_{\rm max} = 6 \ \rm V$.
- This gives the sawtooth-shaped error signal $ε(t)$ between $±1\ \rm V$.
- The period duration is $T_0' = T_0/6$.
(3) The error signal $ε(t)$ proceeds in the same way as $q(t)$ sawtooth.
- Thus, the same equation as in subtask (1) is suitable for calculating the power.
- Note, however, that the amplitude is smaller by a factor $M$ while the different period duration does not matter for the averaging:
- $$P_{\rm Q} = \frac{P_{\rm S}}{M^2} = \frac{12\,{\rm V}^2}{36}\hspace{0.15cm}\underline {= 0.333\,{\rm V}^2 }\hspace{0.05cm}.$$
(4) The results of the subtasks (1) and (3) lead to the quantization SNR:
- $$\rho_{\rm Q} = \frac{P_{\rm S}}{P_{\rm Q}} = M^2 = 36 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm Q}\hspace{0.15cm}\underline { =15.56\,{\rm dB}} \hspace{0.05cm}.$$
(5) With $M = 2^N$ we obtain in general:
- $$ \rho_{\rm Q} = M^2 = 2^{2N} \hspace{0.3cm}\rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm Q} =20 \cdot {\rm lg}\hspace{0.1cm}(2)\cdot N \approx 6.02\,{\rm dB} \cdot N .$$
- This results in the special cases we are looking for:
- $$N = 8:\hspace{0.2cm} 10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm Q} \hspace{0.15cm}\underline {= 48.16\,{\rm dB}}\hspace{0.05cm},$$
- $$N = 16:\hspace{0.2cm} 10 \cdot {\rm lg}\hspace{0.1cm}\rho_{\rm Q} \hspace{0.15cm}\underline { = 96.32\,{\rm dB}}\hspace{0.05cm}.$$
(6) All of the above preconditions must be satisfied:
- For non-linear quantization, the simple relation $ρ_{\rm Q} = M^2$ does not hold.
- For an PDF other than the uniform distribution $ρ_{\rm Q} = M^2$ is also only an approximation, but this is usually accepted.
- If $Q_{\rm max} < q_{\rm max}$, truncation of the peaks occurs, while with $Q_{\rm max} > q_{\rm max}$ the quantization intervals are larger than required.
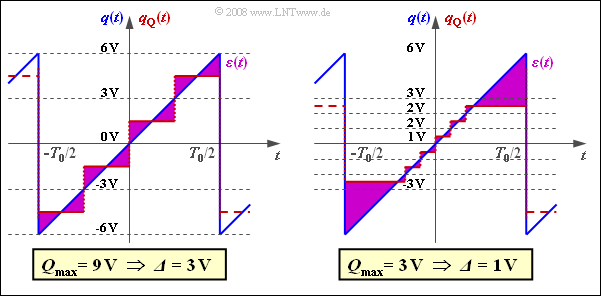
The graph shows the error signals $ε(t)$
- for $Q_{\rm max} > q_{\rm max}$ (left)
- and $Q_{\rm max} < q_{\rm max}$ (right):
- In both cases, the quantization noise power is significantly larger than calculated in sub-task (3).