Difference between revisions of "Aufgaben:Exercise 4.1Z: Other Basis Functions"
| Line 2: | Line 2: | ||
{{quiz-Header|Buchseite=Digital_Signal_Transmission/Signals,_Basis_Functions_and_Vector_Spaces}} | {{quiz-Header|Buchseite=Digital_Signal_Transmission/Signals,_Basis_Functions_and_Vector_Spaces}} | ||
| − | [[File:P_ID1996__Dig_Z_4_1.png|right|frame| | + | [[File:P_ID1996__Dig_Z_4_1.png|right|frame|Energy-limited signals]] |
This exercise pursues exactly the same goal as [[Aufgaben:Aufgabe_4.1:_Zum_Gram-Schmidt-Verfahren|"Exercise 4.1"]]: | This exercise pursues exactly the same goal as [[Aufgaben:Aufgabe_4.1:_Zum_Gram-Schmidt-Verfahren|"Exercise 4.1"]]: | ||
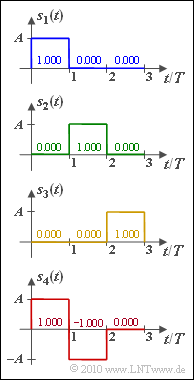
| − | For $M = 4$ energy-limited signals $s_i(t)$ with $i = 1, \ \text{...} \ , 4$, the $N$ required orthonormal basis functions $\varphi_{\it j}(t)$ are to be found, which must satisfy the following condition: | + | For $M = 4$ energy-limited signals $s_i(t)$ with $i = 1, \ \text{...} \ , 4$, the $N$ required orthonormal basis functions $\varphi_{\it j}(t)$ are to be found, which must satisfy the following condition: |
:$$< \hspace{-0.1cm} \varphi_j(t), \hspace{0.1cm}\varphi_k(t) \hspace{-0.1cm} > \hspace{0.1cm} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \int_{-\infty}^{+\infty}\varphi_j(t) \cdot \varphi_k(t)\, {\rm d} t = {\rm \delta}_{jk} = | :$$< \hspace{-0.1cm} \varphi_j(t), \hspace{0.1cm}\varphi_k(t) \hspace{-0.1cm} > \hspace{0.1cm} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \int_{-\infty}^{+\infty}\varphi_j(t) \cdot \varphi_k(t)\, {\rm d} t = {\rm \delta}_{jk} = | ||
\left\{ \begin{array}{c} 1 \\ | \left\{ \begin{array}{c} 1 \\ | ||
| Line 13: | Line 13: | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | With $M$ transmitted signals $s_i(t)$, already fewer basis functions $\varphi_{\it j}(t)$ can suffice, namely $N$. Thus, in general, $N ≤ M$. | + | With $M$ transmitted signals $s_i(t)$, already fewer basis functions $\varphi_{\it j}(t)$ can suffice, namely $N$. Thus, in general, $N ≤ M$. |
These are exactly the same energy-limited signals $s_i(t)$ as in [[Aufgaben:Aufgabe_4.1:_Zum_Gram-Schmidt-Verfahren|"Exercise 4.1"]]: | These are exactly the same energy-limited signals $s_i(t)$ as in [[Aufgaben:Aufgabe_4.1:_Zum_Gram-Schmidt-Verfahren|"Exercise 4.1"]]: | ||
| − | *The difference is the different order of the signals $s_i(t)$. | + | *The difference is the different order of the signals $s_i(t)$. |
| − | *In this exercise, these are sorted in such a way that the basis functions can be found without using the more cumbersome [[Digital_Signal_Transmission/Signals,_Basis_Functions_and_Vector_Spaces#The_Gram-Schmidt_process|"Gram-Schmidt process"]]. | + | |
| − | + | *In this exercise, these are sorted in such a way that the basis functions can be found without using the more cumbersome [[Digital_Signal_Transmission/Signals,_Basis_Functions_and_Vector_Spaces#The_Gram-Schmidt_process|"Gram-Schmidt process"]]. | |
| − | |||
| − | + | Notes: | |
*The exercise belongs to the chapter [[Digital_Signal_Transmission/Signals,_Basis_Functions_and_Vector_Spaces|"Signals, Basis Functions and Vector Spaces"]]. | *The exercise belongs to the chapter [[Digital_Signal_Transmission/Signals,_Basis_Functions_and_Vector_Spaces|"Signals, Basis Functions and Vector Spaces"]]. | ||
| − | *For numerical calculations, use: $A = 1 \sqrt{\rm W} , \hspace{0.2cm} T = 1\,{\rm µ s} \hspace{0.05cm}. $ | + | *For numerical calculations, use: $A = 1 \sqrt{\rm W} , \hspace{0.2cm} T = 1\,{\rm µ s} \hspace{0.05cm}. $ |
===Questions=== | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {In Exercise 4.1, the Gram-Schmidt process resulted in $N = 3$ basis functions. How many basis functions are needed here? | + | {In Exercise 4.1, the Gram-Schmidt process resulted in $N = 3$ basis functions. How many basis functions are needed here? |
|type="{}"} | |type="{}"} | ||
$N \ = \ $ { 3 3% } | $N \ = \ $ { 3 3% } | ||
| − | {Give the 2–norm of all signals: | + | {Give the 2–norm of all these signals: |
|type="{}"} | |type="{}"} | ||
$||s_1(t)|| \ = \ $ { 1 3% } $\ \cdot \ 10^{\rm –3} \ \rm \sqrt{Ws}$ | $||s_1(t)|| \ = \ $ { 1 3% } $\ \cdot \ 10^{\rm –3} \ \rm \sqrt{Ws}$ | ||
| Line 45: | Line 44: | ||
{Which statements are true for the basis functions $\varphi_1(t)$, $\varphi_2(t)$ and $\varphi_3(t)$? | {Which statements are true for the basis functions $\varphi_1(t)$, $\varphi_2(t)$ and $\varphi_3(t)$? | ||
|type="[]"} | |type="[]"} | ||
| − | + The basis functions computed in Exericse 4.1 are also appropriate here. | + | + The basis functions computed in "Exericse 4.1" are also appropriate here. |
| − | - There are infinitely many possibilities for $\{\varphi_1(t), | + | - There are infinitely many possibilities for $\{\varphi_1(t),\ \varphi_2(t),\ \varphi_3(t)\}$. |
| − | - A possible | + | - A possible set is $\{\varphi_{\it j}(t)\} = \{s_{\it j}(t)\}$, with $j = 1,\ 2,\ 3$. |
| − | + A possible | + | + A possible set is $\{\varphi_{\it j}(t)\} = \{s_{\it j}(t)/K\}$, with $j = 1,\ 2,\ 3$. |
| − | {What are the coefficients of the signal $s_4(t)$ | + | {What are the coefficients of the signal $s_4(t)$ with respect to the basis functions $\{\varphi_{\it j}(t)\} = \{s_{\it j}(t)/K\}$, with $j = 1,\ 2,\ 3$? |
|type="{}"} | |type="{}"} | ||
$s_{\rm 41} \ = \ $ { 1 3% } $\ \cdot \ 10^{\rm –3} \ \rm \sqrt{Ws}$ | $s_{\rm 41} \ = \ $ { 1 3% } $\ \cdot \ 10^{\rm –3} \ \rm \sqrt{Ws}$ | ||
Revision as of 13:19, 13 July 2022
This exercise pursues exactly the same goal as "Exercise 4.1":
For $M = 4$ energy-limited signals $s_i(t)$ with $i = 1, \ \text{...} \ , 4$, the $N$ required orthonormal basis functions $\varphi_{\it j}(t)$ are to be found, which must satisfy the following condition:
- $$< \hspace{-0.1cm} \varphi_j(t), \hspace{0.1cm}\varphi_k(t) \hspace{-0.1cm} > \hspace{0.1cm} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \int_{-\infty}^{+\infty}\varphi_j(t) \cdot \varphi_k(t)\, {\rm d} t = {\rm \delta}_{jk} = \left\{ \begin{array}{c} 1 \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} j = k \\ j \ne k \\ \end{array} \hspace{0.05cm}.$$
With $M$ transmitted signals $s_i(t)$, already fewer basis functions $\varphi_{\it j}(t)$ can suffice, namely $N$. Thus, in general, $N ≤ M$.
These are exactly the same energy-limited signals $s_i(t)$ as in "Exercise 4.1":
- The difference is the different order of the signals $s_i(t)$.
- In this exercise, these are sorted in such a way that the basis functions can be found without using the more cumbersome "Gram-Schmidt process".
Notes:
- The exercise belongs to the chapter "Signals, Basis Functions and Vector Spaces".
- For numerical calculations, use: $A = 1 \sqrt{\rm W} , \hspace{0.2cm} T = 1\,{\rm µ s} \hspace{0.05cm}. $
Questions
Solution
- Thus it is obvious that $\underline {N = 3}$ must hold here as well.
(2) The 2–norm gives the root of the signal energy and is comparable to the rms value for power-limited signals.
- The first three signals all have the 2–norm
- $$||s_1(t)|| = ||s_2(t)|| = ||s_3(t)|| = \sqrt{A^2 \cdot T}\hspace{0.1cm}\hspace{0.15cm}\underline { = 10^{-3}\sqrt{\rm Ws}} \hspace{0.05cm}.$$
- The norm of the last signal is larger by a factor of $\sqrt{2}$:
- $$||s_4(t)|| \hspace{0.1cm}\hspace{0.15cm}\underline { = 1.414 \cdot 10^{-3}\sqrt{\rm Ws}} \hspace{0.05cm}.$$
Basisfunktionssatz (3) The first and last statements are true in contrast to statements 2 and 3:
- It would be completely illogical if the basis functions found should no longer hold when the signals $s_i(t)$ are sorted differently.
- The Gram–Schmidt process yields only one possible set $\{\varphi_{\it j}(t)\}$ of basis functions. A different sorting (possibly) yields a different one.
- The number of permutations of $M = 4$ signals is $4! = 24$. In any case, there cannot be more basis function sets ⇒ solution 2 is wrong.
- However, there are probably (because of $N = 3$) only $3! = 6$ possible sets of basis functions. As can be seen from the sample "solution" to Exercise 4.1, the same basis functions will result with the order $s_1(t), s_2(t), s_4(t), s_3(t)$ as with $s_1(t), s_2(t), s_3(t), s_4(t)$. However, this is only a conjecture of the authors; we have not checked it.
- Statement 3 cannot be true simply because of the different units of $s_i(t)$ and $\varphi_{\it j}(t)$. Like $A$, the signals have the unit $\sqrt{\rm W}$, the basis functions the unit $\sqrt{\rm 1/s}$.
- Thus, the last solution is correct, where for $K$ holds:
- $$K = ||s_1(t)|| = ||s_2(t)|| = ||s_3(t)|| = 10^{-3}\sqrt{\rm Ws} \hspace{0.05cm}.$$
Ende Basisfunktionssatz
(4) From the comparison of the diagrams in the specification section we can see:
- $$s_{4}(t) = s_{1}(t) - s_{2}(t) = K \cdot \varphi_1(t) - K \cdot \varphi_2(t)\hspace{0.05cm}.$$
- Furthermore holds:
- $$s_{4}(t) = s_{41}\cdot \varphi_1(t) + s_{42}\cdot \varphi_2(t) + s_{43}\cdot \varphi_3(t)$$
- $$\Rightarrow \hspace{0.3cm}s_{41} = K \hspace{0.1cm}\hspace{0.15cm}\underline {= 10^{-3}\sqrt{\rm Ws}}\hspace{0.05cm}, \hspace{0.2cm}s_{42} = -K \hspace{0.1cm}\hspace{0.15cm}\underline {= -10^{-3}\sqrt{\rm Ws}}\hspace{0.05cm}, \hspace{0.2cm}s_{43} \hspace{0.1cm}\hspace{0.15cm}\underline { = 0}\hspace{0.05cm}. $$