Aufgaben:Exercise 4.15: Optimal Signal Space Allocation

• Return to book

Considered 8–QAM

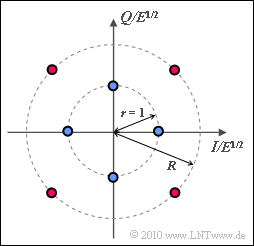
A signal space constellation with  $M = 8$  signal space points is considered here:

• Four points lie on a circle with radius  $r = 1$.
• Four further points lie offset by  $45^\circ$  on a second circle with radius  $R$, where the following shall hold:

$$R_{\rm min} \le R \le R_{\rm max}\hspace{0.05cm},\hspace{0.2cm} R_{\rm min}= \frac{ \sqrt{3}-1}{ \sqrt{2}} \approx 0.518 \hspace{0.05cm},\hspace{0.2cm} R_{\rm max}= \frac{ \sqrt{3}+1}{ \sqrt{2}} \approx 1.932\hspace{0.05cm}.$$

Let the two axes (basis functions) be normalized respectively and denoted  $I$  and  $Q$  for simplicity. For further simplification,  $E = 1$  can be set.

In the question section, we speak of blue and red points. According to the diagram, the blue points lie on the circle with radius  $r = 1$, the red points on the circle with radius  $R$. The case  $R = R_{\rm max}$ is drawn.

The system parameter  $R$  is to be determined in this exercise in such a way that the quotient

$$\eta = \frac{ (d_{\rm min}/2)^2}{ E_{\rm B}} $$

becomes maximum. $\eta$  is a measure for the quality of a modulation alphabet at given transmission energy per bit ("Power Efficiency"). It is calculated from

• the minimum distance  $d_{\rm min}$, and
• the bit energy  $E_{\rm B}$.

It must be ensured that  $d_{\rm min}^2$  and  $E_{\rm B}$  are normalized in the same way, but this is already implicit in the exercise.

Notes:

• The exercise belongs to the chapter  "Carrier Frequency Systems with Coherent Demodulation".
• Reference is made in particular to the sections  "Quadrature amplitude modulation"  and  "Multilevel phase modulation".

Questions

1

Berechnen Sie die mittlere Energie  $E_{\rm B}$  pro Bit abhängig von  $R$, insbesondere für  $R = 1$  und  $R = \sqrt{2}$.

$R = 1 \text{:} \hspace{0.55cm} E_{\rm B}\ = \ $

$R = \sqrt{2} \text{:} \hspace{0.2cm} E_{\rm B}\ = \ $

2

Welche Aussagen gelten für den minimalen Abstand zweier Signalraumpunkte?

	Für  $R < R_{\rm min}$  tritt die minimale Distanz zwischen zwei roten Punkten auf.
	Für  $R > R_{\rm max}$  tritt die minimale Distanz zwischen zwei blauen Punkten auf.
	Für  $R_{\rm min} ≤ R ≤ R_{\rm max}$  tritt die minimale Distanz zwischen "Rot" und "Blau" auf.

3

Berechnen Sie die minimale Distanz abhängig von  $R$, insbesondere für

$R = 1 \text{:} \hspace{0.55cm} d_{\rm min}\ = \ $

$R = \sqrt{2} \text{:} \hspace{0.2cm} d_{\rm min}\ = \ $

4

Geben Sie die Leistungseffizienz  $\eta$  allgemein an. Welches  $\eta$  ergibt sich für  $R = 1$?

$\eta\ = \ $

5

Welche Leistungseffizienzwerte ergeben sich für  $R = R_{\rm min}$  und  $R = R_{\rm max}$? Interpretation.

$R = R_{\rm min} \text{:} \hspace{0.35cm} \eta\ = \ $

$R = R_{\rm max} \text{:} \hspace{0.2cm} \eta\ = \ $

Musterlösung

Solution

(1)  Wegen $M = 8$  ⇒  $b = 3$ gilt für die mittlere Signalenergie pro Bit $E_{\rm B} = E_{\rm S}/3$, wobei die mittlere Signalenergie pro Symbol ($E_{\rm S}$) als der mittlere quadratische Abstand der Signalraumpunkte vom Ursprung zu berechnen ist. Mit $r = 1$ erhält man:

Sonderfälle der 8–QAM

$$E_{\rm S} = {1}/{8 } \cdot ( 4 \cdot r^2 + 4 \cdot R^2) = ({1 + R^2})/{2 } \hspace{0.3cm}\Rightarrow \hspace{0.3cm} E_{\rm B} = {E_{\rm S}}/{3} = ({1 + R^2})/{6} \hspace{0.05cm}.$$

Insbesondere gilt:

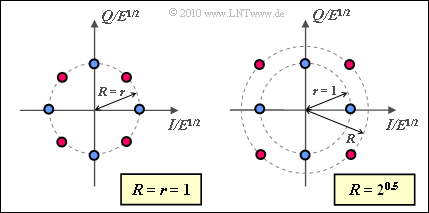
• Für $R = 1$ ergibt sich eine 8–PSK   ⇒   $E_{\rm S} = 1$ und $E_{\rm B} \ \underline {= 0.333}$ (siehe linke Grafik).
• Die rechte Grafik gilt für $R = \sqrt{2}$. In diesem Fall ist $E_{\rm B} \ \underline {= 0.5}$.

Anzumerken ist, dass diese Energien eigentlich noch mit der Normierungsenergie $E$ zu multiplizieren sind.

(2)  Alle Aussagen treffen zu:

• Im gezeichneten Beispiel auf dem Angabenblatt mit $R = R_{\rm max}$ ist der Abstand zwischen zwei benachbarten blauen Punkten genau so groß wie der Abstand zwischen einem roten (äußeren) und einem blauen (inneren) Punkt.

Zur Berechnung der minimalen Distanz

• Für $R > R_{\rm max}$ ist der Abstand zwischen zwei blauen Punkten am geringsten.
• Für $R < R_{\rm min}$ tritt der minimale Abstand zwischen zwei roten Punkten auf.

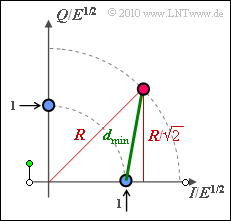
(3)  Die Grafik verdeutlicht die geometrische Berechnung. Mit "Pythagoras" erhält man:

$$d_{\rm min}^2 =(R/\sqrt{2})^2 + (R/\sqrt{2}-1)^2 = 1 - \sqrt{2} \cdot R + R^2 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}d_{\rm min} = \sqrt{ 1 - \sqrt{2} \cdot R + R^2} \hspace{0.05cm}.$$

Insbesondere gilt für $R = 1$ (8–PSK):

$$d_{\rm min} = \sqrt{ 2 - \sqrt{2} } \hspace{0.1cm} \underline{= 0.765} \hspace{0.1cm} (= 2 \cdot \sin (22.5^{\circ}) ) \hspace{0.05cm}.$$

Dagegen ist für $\underline {R = \sqrt{2}}$ entsprechend der rechten Grafik zur Teilaufgabe (1) die minimale Distanz $d_{\rm min} \ \underline {= 1}$.

(4)  Mit den Ergebnissen von (1) und (3) erhält man allgemein bzw. für $R = 1$ (8–PSK):

$$\eta = \frac{ d_{\rm min}^2}{ 4 \cdot E_{\rm B}} = \frac{ 1 - \sqrt{2} \cdot R + R^2}{ 4 \cdot (1 + R^2)/6} = \frac{ 3/2 \cdot(1 - \sqrt{2} \cdot R + R^2)}{ 1 + R^2}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} R = 1: \hspace{0.2cm}\eta = \frac{ 3/2 \cdot(2 - \sqrt{2}) }{ 2} = 3/4 \cdot(2 - \sqrt{2})\hspace{0.1cm} \underline{\approx 0.439}\hspace{0.05cm}.$$

(5)  Für $R = R_{\rm min} = (\sqrt{3}-1)/\sqrt{2}$ ergibt sich folgender Wert:

$$\eta = \frac{ 3/2 \cdot(1 - \sqrt{2} \cdot R + R^2)}{ 1 + R^2} = 3/2 \cdot \left [ 1 - \frac{ \sqrt{2} \cdot R }{ 1 + R^2}\right ]\hspace{0.05cm},$$

$$\sqrt{2} \cdot R = \sqrt{3}- 1\hspace{0.05cm},\hspace{0.2cm} 1 + R^2 = 3 - \sqrt{3} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \eta = 3/2 \cdot \left [ 1 - \frac{ \sqrt{3}- 1 }{ 3 - \sqrt{3}}\right ]\hspace{0.1cm} \underline{\approx 0.634}\hspace{0.05cm}.$$

Für $R = R_{\rm max}= (\sqrt{3}+1)/\sqrt{2}$ ergibt sich genau der gleiche Wert.

• Das (stets gewünschte) Maximum der Leistungseffizienz $\eta$ ergibt sich beispielsweise für $R = R_{\rm max}$ – also für die Signalraumkonstellation auf dem Angabenblatt.
• In diesem Fall sind alle Dreiecke aus zwei benachbarten blauen Punkten und dem dazwischenliegenden roten Punkt gleichseitig.
• Auch für $R = R_{\rm min}$ ergeben sich gleichseitige Dreiecke, jetzt aber jeweils gebildet durch zwei rotee und einen blauen Punkt.
• In diesem Fall ist zwar die Kantenlänge $d_{\rm min}$ deutlich kleiner, aber gleichzeitig ergibt sich auch ein kleineres $E_{\rm B}$, so dass die Leistungseffizienz $\eta$ den gleichen Wert besitzt.

Die vorher betrachteten Sonderfälle $R = 1$ (8–PSK, linke Grafik bei der ersten Teilaufgabe) und $R = \sqrt{2}$ (rechte Grafik) weisen mit $\eta = 0.439$ bzw. $\eta = 0.5$ (gegenüber $\eta = 0.634$) ein merklich kleineres $\eta$ auf.