Difference between revisions of "Aufgaben:Exercise 2.5Z: Some Calculations about GF(2 power 3)"
m (Text replacement - "Category:Aufgaben zu Kanalcodierung" to "Category:Channel Coding: Exercises") |
|||
| Line 1: | Line 1: | ||
{{quiz-Header|Buchseite=Kanalcodierung/Erweiterungskörper}} | {{quiz-Header|Buchseite=Kanalcodierung/Erweiterungskörper}} | ||
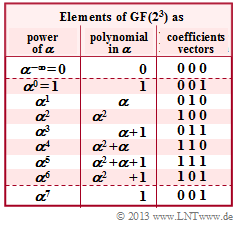
| − | [[File: | + | [[File:EN_KC_Z_2_5.png|right|frame|Elemente von $\rm GF(2^3)$ für das Polynom $p(x) = x^3 + x + 1$]] |
Wir betrachten nun den Erweiterungskörper (englisch: <i>Extension Field</i> ) mit acht Elementen ⇒ $\rm GF(2^3)$ gemäß der nebenstehenden Tabelle. Da das zugrunde liegende Polynom | Wir betrachten nun den Erweiterungskörper (englisch: <i>Extension Field</i> ) mit acht Elementen ⇒ $\rm GF(2^3)$ gemäß der nebenstehenden Tabelle. Da das zugrunde liegende Polynom | ||
:$$p(x) = x^3 + x +1 $$ | :$$p(x) = x^3 + x +1 $$ | ||
Revision as of 14:00, 22 August 2022
Wir betrachten nun den Erweiterungskörper (englisch: Extension Field ) mit acht Elementen ⇒ $\rm GF(2^3)$ gemäß der nebenstehenden Tabelle. Da das zugrunde liegende Polynom
- $$p(x) = x^3 + x +1 $$
sowohl irreduzibel als auch primitiv ist, kann das vorliegende Galoisfeld in folgender Form angegeben werden:
- $${\rm GF}(2^3) = \{\hspace{0.1cm}0\hspace{0.05cm},\hspace{0.1cm} 1,\hspace{0.05cm}\hspace{0.1cm} \alpha\hspace{0.05cm},\hspace{0.1cm} \alpha^{2}\hspace{0.05cm},\hspace{0.1cm} \alpha^{3}\hspace{0.05cm},\hspace{0.1cm} \alpha^{4}\hspace{0.05cm},\hspace{0.1cm} \alpha^{5}\hspace{0.05cm},\hspace{0.1cm} \alpha^{6}\hspace{0.1cm}\}\hspace{0.05cm}. $$
Das Element $\alpha$ ergibt sich dabei als Lösung der Gleichung $p(\alpha) = 0$ im Galoisfeld $\rm GF(2)$.
- Damit erhält man folgende Nebenbedingung:
- $$\alpha^3 + \alpha +1 = 0\hspace{0.3cm} \Rightarrow\hspace{0.3cm} \alpha^3 = \alpha +1\hspace{0.05cm}.$$
- Für die weiteren Elemente gelten folgende Berechnungen:
- $$\alpha^4 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha \cdot \alpha^3 = \alpha \cdot (\alpha + 1) = \alpha^2 + \alpha \hspace{0.05cm},$$
- $$\alpha^5 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha \cdot \alpha^4 = \alpha \cdot (\alpha^2 +\alpha) = \alpha^3 + \alpha^2 = \alpha^2 + \alpha + 1\hspace{0.05cm},$$
- $$\alpha^6 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha \cdot \alpha^5 = \alpha \cdot (\alpha^2 +\alpha + 1)= \alpha^3 + \alpha^2 + \alpha= \alpha + 1 + \alpha^2 + \alpha = \alpha^2+ 1\hspace{0.05cm}.$$
In dieser Aufgabe sollen Sie einige algebraische Umformungen im Galoisfeld $\rm GF(2^3)$ vornehmen. Unter anderem ist nach der multiplikativen Inversen des Elementes $\alpha^4$ gefragt. Dann muss gelten:
- $$\alpha^4 \cdot {\rm Inv_M}( \alpha^4) = 1 \hspace{0.05cm}.$$
Hinweise:
- Die Aufgabe gehört zum Kapitel Erweiterungskörper.
- Diese Aufgabe ist als Ergänzung zur etwas schwierigeren Aufgabe 2.5 gedacht.
Fragebogen
Musterlösung
- $$\alpha^7 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha \cdot \alpha^6 = \alpha \cdot (\alpha^2 + 1) = \alpha^3 + \alpha = (\alpha + 1) + \alpha = 1 \hspace{0.05cm},$$
- $$\alpha^8 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha \cdot \alpha^7 = \alpha \cdot 1 = \alpha\hspace{0.05cm},$$
- $$\alpha^{13} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha^7 \cdot \alpha^6 = 1 \cdot \alpha^6 = \alpha^2 + 1\hspace{0.05cm}.$$
Die Tabelle lässt sich also modulo $7$ fortsetzen. Das bedeutet: Alle Lösungsvorschläge sind richtig.
(2) Richtig ist der Lösungsvorschlag 2 wegen
- $\alpha^8 = \alpha$ entsprechend Teilaufgabe (1),
- $\alpha^6 = \alpha^2 + 1$ (gemäß Tabelle), und
- $-\alpha^2 = \alpha^2$ (Operationen im binären Galoisfeld).
Also gilt:
- $$A = \alpha^8 + \alpha^6 - \alpha^2 + 1 = \alpha + (\alpha^2 + 1) + \alpha^2 + 1 = \alpha \hspace{0.05cm}.$$
(3) Mit $\alpha^{16} = \alpha^{16-14} = \alpha^2$ sowie $\alpha^{12} \cdot \alpha^3 = \alpha^{15} = \alpha^{15-14} = \alpha$ erhält man den Lösungsvorschlag 5:
- $$B = \alpha^2 + \alpha= \alpha^4 \hspace{0.05cm}.$$
(4) Es gilt $\alpha^3 = \alpha + 1$ und damit $C = \alpha^3 + \alpha = \alpha + 1 + \alpha = 1$ ⇒ Lösungsvorschlag 1.
(5) Mit $\alpha^4 = \alpha^2 + \alpha$ erhält man $D = \alpha^4 + \alpha = \alpha^2$ ⇒ Lösungsvorschlag 3.
(6) Richtig ist der Lösungsvorschlag 4:
- $$E = A \cdot B \cdot C/D = \alpha \cdot \alpha^4 \cdot 1/\alpha^2 = \alpha^3 \hspace{0.05cm}.$$
(7) Laut Tabelle gilt $\alpha^2 + \alpha = \alpha^4$. Deshalb muss gelten:
- $$\alpha^4 \cdot {\rm Inv_M}( \alpha^4) = 1 \hspace{0.3cm} \Rightarrow\hspace{0.3cm} {\rm Inv_M}( \alpha^2 + \alpha) = {\rm Inv_M}( \alpha^4) = \alpha^{-4} = \alpha^3 \hspace{0.05cm}.$$
Wegen $\alpha^3 = \alpha + 1$ sind somit die Lösungsvorschläge 2 und 3 richtig.