Difference between revisions of "Aufgaben:Exercise 2.2: Properties of Galois Fields"
| Line 4: | Line 4: | ||
Here we consider the sets of numbers | Here we consider the sets of numbers | ||
* $Z_5 = \{0, \, 1, \, 2, \, 3, \, 4\} \ \Rightarrow \ q = 5$, | * $Z_5 = \{0, \, 1, \, 2, \, 3, \, 4\} \ \Rightarrow \ q = 5$, | ||
| + | |||
* $Z_6 = \{0, \, 1, \, 2, \, 3, \, 4,\, 5\} \ \Rightarrow \ q = 6$. | * $Z_6 = \{0, \, 1, \, 2, \, 3, \, 4,\, 5\} \ \Rightarrow \ q = 6$. | ||
| − | In the adjacent graph, the (partially incomplete) | + | In the adjacent graph, the (partially incomplete) addition and multiplication tables for $q = 5$ and $q = 6$ are given, where both addition ("$+$") and multiplication ("$\hspace{0.05cm}\cdot\hspace{0.05cm}$") modulo $q$ are to be understood. |
| − | To be checked is whether the sets | + | To be checked is whether the number sets $Z_5$ and $Z_6$ satisfy all the conditions of a Galois field $\rm GF(5)$ and $\rm GF(6)$, respectively. |
| − | In the [[Channel_Coding/Some_Basics_of_Algebra#Definition_of_a_Galois_field|"theory section"]] a total of eight conditions are mentioned, all of which must be met. You are to check only two of these conditions: | + | In the [[Channel_Coding/Some_Basics_of_Algebra#Definition_of_a_Galois_field|"theory section"]] a total of eight conditions are mentioned, all of which must be met. You are to check only two of these conditions: |
| − | $\rm(D)$ For all elements there is an <b>additive inverse</b> ( | + | $\rm(D)$ For all elements there is an <b>additive inverse</b> (Inverse for "$+$"): |
:$$\forall \hspace{0.15cm} z_i \in {\rm GF}(q),\hspace{0.15cm} \exists \hspace{0.15cm} {\rm Inv_A}(z_i) \in {\rm GF}(q)\text{:}\hspace{0.5cm}z_i + {\rm Inv_A}(z_i) = 0 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} | :$$\forall \hspace{0.15cm} z_i \in {\rm GF}(q),\hspace{0.15cm} \exists \hspace{0.15cm} {\rm Inv_A}(z_i) \in {\rm GF}(q)\text{:}\hspace{0.5cm}z_i + {\rm Inv_A}(z_i) = 0 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} | ||
{\rm Inv_A}(z_i) = -z_i \hspace{0.05cm}.$$ | {\rm Inv_A}(z_i) = -z_i \hspace{0.05cm}.$$ | ||
| − | $\rm(E)$ All elements have a <b>multiplicative inverse</b> ( | + | $\rm(E)$ All elements have a <b>multiplicative inverse</b> (Inverse for "$\hspace{0.05cm}\cdot\hspace{0.05cm}$"): |
:$$\forall \hspace{0.15cm} z_i \in {\rm GF}(q),\hspace{0.15cm} z_i \ne 0, \hspace{0.15cm} \exists \hspace{0.15cm} {\rm Inv_M}(z_i) \in {\rm GF}(q)\text{:}\hspace{0.5cm}z_i \cdot {\rm Inv_M}(z_i) = 1 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} | :$$\forall \hspace{0.15cm} z_i \in {\rm GF}(q),\hspace{0.15cm} z_i \ne 0, \hspace{0.15cm} \exists \hspace{0.15cm} {\rm Inv_M}(z_i) \in {\rm GF}(q)\text{:}\hspace{0.5cm}z_i \cdot {\rm Inv_M}(z_i) = 1 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} | ||
{\rm Inv_M}(z_i) = z_i^{-1}\hspace{0.05cm}.$$ | {\rm Inv_M}(z_i) = z_i^{-1}\hspace{0.05cm}.$$ | ||
| Line 24: | Line 25: | ||
* Closure, | * Closure, | ||
* Existence of zero– and identity element, | * Existence of zero– and identity element, | ||
| − | * validity of commutative | + | * validity of commutative law, associative law and distributive law |
| − | |||
| − | |||
| − | |||
| + | are satisfied by both, $Z_5$ and $Z_6$. | ||
| Line 35: | Line 34: | ||
| − | Hints: | + | Hints: The exercise refers to the chapter [[Channel_Coding/Some_Basics_of_Algebra| "Some Basics of Algebra"]]. |
| − | |||
| Line 43: | Line 41: | ||
===Questions=== | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Complete the addition table for $q = 5$. Enter the following values: | + | {Complete the addition table for $q = 5$. Enter the following values: |
|type="{}"} | |type="{}"} | ||
$A_{04} \ = \ ${ 4 } | $A_{04} \ = \ ${ 4 } | ||
| Line 49: | Line 47: | ||
$A_{44} \ = \ ${ 3 } | $A_{44} \ = \ ${ 3 } | ||
| − | {Complete the multiplication table for $q = 5$. Enter the following values: | + | {Complete the multiplication table for $q = 5$. Enter the following values: |
|type="{}"} | |type="{}"} | ||
$M_{04} \ = \ ${ 0. } | $M_{04} \ = \ ${ 0. } | ||
| Line 55: | Line 53: | ||
$M_{44} \ = \ ${ 1. } | $M_{44} \ = \ ${ 1. } | ||
| − | {Does the | + | {Does the $Z_5$ set satisfy the conditions of a Galois field? |
|type="[]"} | |type="[]"} | ||
+ Yes. | + Yes. | ||
| − | - No, there is not an additive inverse for all elements $(0, \hspace{0.05cm}\text{...} \hspace{0.1cm}, 4)$ . | + | - No, there is not an additive inverse for all elements $(0, \hspace{0.05cm}\text{...} \hspace{0.1cm}, 4)$ . |
| − | - No, the elements $1, \hspace{0.05cm}\text{...} \hspace{0.1cm}, 4$ do not all have a multiplicative inverse. | + | - No, the elements $1, \hspace{0.05cm}\text{...} \hspace{0.1cm}, 4$ do not all have a multiplicative inverse. |
| − | {Does the | + | {Does the $Z_6$ set satisfy the conditions of a Galois field? |
|type="[]"} | |type="[]"} | ||
- Yes. | - Yes. | ||
| − | - No, there is not an additive inverse for all elements $(0, \hspace{0.05cm}\text{...} \hspace{0.1cm}, 5)$ . | + | - No, there is not an additive inverse for all elements $(0, \hspace{0.05cm}\text{...} \hspace{0.1cm}, 5)$ . |
| − | + No, the elements $1, \hspace{0.05cm}\text{...} \hspace{0.1cm}, 5$ do not all have a multiplicative inverse. | + | + No, the elements $1, \hspace{0.05cm}\text{...} \hspace{0.1cm}, 5$ do not all have a multiplicative inverse. |
| − | {The sets | + | {The number sets $Z_2, \ Z_3, \ Z_5$ and $Z_7$ yield a Galois field, but the sets $Z_4, \ Z_6, \ Z_8, \ Z_9$ do not. What do you conclude from this? |
|type="[]"} | |type="[]"} | ||
- $Z_{10} = \{0, \, 1, \, 2, \, 3, \, 4, \, 5, \, 6, \, 7, \, 8, \, 9\}$ is a Galois field? | - $Z_{10} = \{0, \, 1, \, 2, \, 3, \, 4, \, 5, \, 6, \, 7, \, 8, \, 9\}$ is a Galois field? | ||
Revision as of 13:39, 28 August 2022
Here we consider the sets of numbers
- $Z_5 = \{0, \, 1, \, 2, \, 3, \, 4\} \ \Rightarrow \ q = 5$,
- $Z_6 = \{0, \, 1, \, 2, \, 3, \, 4,\, 5\} \ \Rightarrow \ q = 6$.
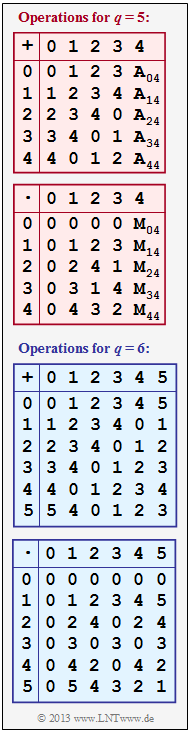
In the adjacent graph, the (partially incomplete) addition and multiplication tables for $q = 5$ and $q = 6$ are given, where both addition ("$+$") and multiplication ("$\hspace{0.05cm}\cdot\hspace{0.05cm}$") modulo $q$ are to be understood.
To be checked is whether the number sets $Z_5$ and $Z_6$ satisfy all the conditions of a Galois field $\rm GF(5)$ and $\rm GF(6)$, respectively.
In the "theory section" a total of eight conditions are mentioned, all of which must be met. You are to check only two of these conditions:
$\rm(D)$ For all elements there is an additive inverse (Inverse for "$+$"):
- $$\forall \hspace{0.15cm} z_i \in {\rm GF}(q),\hspace{0.15cm} \exists \hspace{0.15cm} {\rm Inv_A}(z_i) \in {\rm GF}(q)\text{:}\hspace{0.5cm}z_i + {\rm Inv_A}(z_i) = 0 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} {\rm Inv_A}(z_i) = -z_i \hspace{0.05cm}.$$
$\rm(E)$ All elements have a multiplicative inverse (Inverse for "$\hspace{0.05cm}\cdot\hspace{0.05cm}$"):
- $$\forall \hspace{0.15cm} z_i \in {\rm GF}(q),\hspace{0.15cm} z_i \ne 0, \hspace{0.15cm} \exists \hspace{0.15cm} {\rm Inv_M}(z_i) \in {\rm GF}(q)\text{:}\hspace{0.5cm}z_i \cdot {\rm Inv_M}(z_i) = 1 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} {\rm Inv_M}(z_i) = z_i^{-1}\hspace{0.05cm}.$$
The other conditions for a Galois field, viz.
- Closure,
- Existence of zero– and identity element,
- validity of commutative law, associative law and distributive law
are satisfied by both, $Z_5$ and $Z_6$.
Hints: The exercise refers to the chapter "Some Basics of Algebra".
Questions
Solution
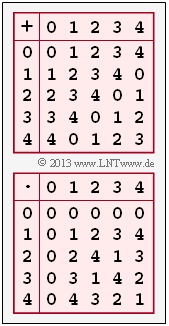
- $$A_{04} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} (0+4) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 \hspace{0.15cm}\underline{= 4}\hspace{0.05cm},\hspace{0.2cm}A_{14}=(1+4) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 \hspace{0.15cm}\underline{= 0}\hspace{0.05cm},\hspace{0.2cm}A_{24}=(2+4) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 1\hspace{0.05cm},$$
- $$A_{34} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} (3+4)\hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5= 2\hspace{0.05cm},\hspace{0.2cm}A_{44}=(4+4) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 \hspace{0.15cm}\underline{= 3}\hspace{0.05cm}.$$
Due to the commutative law of addition,
- $$z_i + z_j = z_j + z_i \hspace{0.5cm} {\rm for \hspace{0.2cm}alle\hspace{0.2cm} } z_i, z_j \in Z_5\hspace{0.05cm},$$
the last column of the addition table is of course identical to the last row of the same table.
(2) Now $M_{\mu 4} = (\mu \cdot 4) \, {\rm mod} \, 5$ and we obtain:
- $$M_{04} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} (0\cdot4) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 \hspace{0.15cm}\underline{= 0}\hspace{0.05cm},\hspace{0.2cm}M_{14}=(1\cdot4) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 \hspace{0.15cm}\underline{= 4}\hspace{0.05cm},\hspace{0.2cm}M_{24}=(2\cdot4) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 3\hspace{0.05cm},$$
- $$M_{34} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} (3\cdot4)\hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 2\hspace{0.05cm},\hspace{0.2cm}M_{44}=(4\cdot 4) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 \hspace{0.15cm}\underline{= 1}\hspace{0.05cm}.$$
Since multiplication is also commutative, the last column in the multiplication table again matches the last row.
(3) The graph shows the full addition and multiplication tables for $q = 5$. You can see:
- In the addition table there is exactly one zero in each row (and also in each column). So for every $z_i ∈ Z_5$ there is a ${\rm Inv}_{\rm A} (z_i)$ that satisfies the condition $[z_i + {\rm Inv}_{\rm A}(z_i)] \, {\rm mod} \, 5 = 0$:
- $$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 0\hspace{0.25cm} \Rightarrow \hspace{0.25cm}{\rm Inv_A}(z_i) = 0 \hspace{0.05cm},$$
- $$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 1\hspace{0.25cm} \Rightarrow \hspace{0.25cm}{\rm Inv_A}(z_i) = (-1) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 4 \hspace{0.05cm},$$
- $$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 2\hspace{0.25cm} \Rightarrow \hspace{0.25cm}{\rm Inv_A}(z_i) = (-2) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 3 \hspace{0.05cm},$$
- $$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 3\hspace{0.25cm} \Rightarrow \hspace{0.25cm}{\rm Inv_A}(z_i) = (-3) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 2 \hspace{0.05cm},$$
- $$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 4\hspace{0.25cm} \Rightarrow \hspace{0.25cm}{\rm Inv_A}(z_i) = (-4) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 1 \hspace{0.05cm}.$$
- In the multiplication table we leave the zero element (first row and first column) out of consideration. In all other rows and columns of the lower table there is indeed exactly one one each. From the condition $[z_i \cdot {\rm Inv}_{\rm M}(z_i)] \, {\rm mod} \, 5 = 1$ one obtains:
- $$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 1 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} {\rm Inv_M}(z_i) = 1 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} z_i \cdot {\rm Inv_M}(z_i) = 1\hspace{0.05cm},$$
- $$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 2 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} {\rm Inv_M}(z_i) = 3 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} z_i \cdot {\rm Inv_M}(z_i) = 6 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 1 \hspace{0.05cm},$$
- $$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 3 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} {\rm Inv_M}(z_i) = 2 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} z_i \cdot {\rm Inv_M}(z_i) = 6 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 1 \hspace{0.05cm},$$
- $$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 4 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} {\rm Inv_M}(z_i) = 4 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} z_i \cdot {\rm Inv_M}(z_i) = 16 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 5 = 1 \hspace{0.05cm}.$$
Since both the required additive and multiplicative inverses exist $Z_5$ describes a Galois field $\rm GF(5)$
⇒ Correct is the proposed solution 1.
(4) From the blue addition table on the statement page, we see that all numbers $0, \, 1, \, 2, \, 3, \, 4, \, 5$ of the set $Z_6$ have an additive inverse ⇒ in each row (and column) there is exactly one zero.
On the other hand, a multiplicative inverse ${\rm Inv}_{\rm M}(z_i)$ exists only for $z_i = 1$ and $z_i = 5$, viz.
- $$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 1 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} {\rm Inv_M}(z_i) = 1 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} z_i \cdot {\rm Inv_M}(z_i) = 1\hspace{0.05cm},$$
- $$z_i \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 5 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} {\rm Inv_M}(z_i) = 5 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} z_i \cdot {\rm Inv_M}(z_i) = 25 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 6 = 1 \hspace{0.05cm}.$$
On the other hand, for $z_i = 2, \ z_i = 3$ and $z_i = 4$, we find no element $z_j$, so that $(z_i \cdot z_j) \, {\rm mod} \, 6 = 1$.
So proposed solution 3 is correct ⇒ The blue tables for $q = 6$ do not yield a Galois field $\rm GF(6)$.
(5) Correct is the proposed solution 2:
- A finite number set $Z_q = \{0, \, 1, \hspace{0.05cm} \text{...} \hspace{0.1cm} , \, q-1\}$ of natural numbers leads to a Galois field only if $q$ is a prime number.
- Of the sets of numbers mentioned above, this is true only for $Z_{11}$.