Difference between revisions of "Aufgaben:Exercise 2.5Z: Some Calculations about GF(2 power 3)"
| Line 1: | Line 1: | ||
{{quiz-Header|Buchseite=Channel_Coding/Extension_Field}} | {{quiz-Header|Buchseite=Channel_Coding/Extension_Field}} | ||
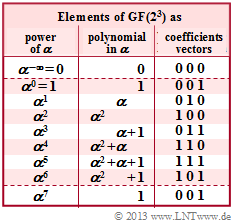
| − | [[File: | + | [[File:EN_KC_Z_2_5_neu.png|right|frame| $\rm GF(2^3)$ elements; polynomial $p(x) = x^3 + x + 1$]] |
We now consider the extension field with eight elements ⇒ $\rm GF(2^3)$ according to the adjacent table. Since the underlying polynomial | We now consider the extension field with eight elements ⇒ $\rm GF(2^3)$ according to the adjacent table. Since the underlying polynomial | ||
:$$p(x) = x^3 + x +1 $$ | :$$p(x) = x^3 + x +1 $$ | ||
| + | |||
| + | EN_KC_Z_2_5.png | ||
is both irreducible and primitive, the Galois field at hand can be stated in the following form: | is both irreducible and primitive, the Galois field at hand can be stated in the following form: | ||
Revision as of 16:19, 30 September 2022
We now consider the extension field with eight elements ⇒ $\rm GF(2^3)$ according to the adjacent table. Since the underlying polynomial
- $$p(x) = x^3 + x +1 $$
EN_KC_Z_2_5.png
is both irreducible and primitive, the Galois field at hand can be stated in the following form:
- $${\rm GF}(2^3) = \{\hspace{0.1cm}0\hspace{0.05cm},\hspace{0.1cm} 1,\hspace{0.05cm}\hspace{0.1cm} \alpha\hspace{0.05cm},\hspace{0.1cm} \alpha^{2}\hspace{0.05cm},\hspace{0.1cm} \alpha^{3}\hspace{0.05cm},\hspace{0.1cm} \alpha^{4}\hspace{0.05cm},\hspace{0.1cm} \alpha^{5}\hspace{0.05cm},\hspace{0.1cm} \alpha^{6}\hspace{0.1cm}\}\hspace{0.05cm}. $$
The element $\alpha$ results thereby as solution of the equation $p(\alpha) = 0$ in the Galois field $\rm GF(2)$.
- This gives the following constraint:
- $$\alpha^3 + \alpha +1 = 0\hspace{0.3cm} \Rightarrow\hspace{0.3cm} \alpha^3 = \alpha +1\hspace{0.05cm}.$$
- The following calculations apply to the other elements:
- $$\alpha^4 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha \cdot \alpha^3 = \alpha \cdot (\alpha + 1) = \alpha^2 + \alpha \hspace{0.05cm},$$
- $$\alpha^5 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha \cdot \alpha^4 = \alpha \cdot (\alpha^2 +\alpha) = \alpha^3 + \alpha^2 = \alpha^2 + \alpha + 1\hspace{0.05cm},$$
- $$\alpha^6 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha \cdot \alpha^5 = \alpha \cdot (\alpha^2 +\alpha + 1)= \alpha^3 + \alpha^2 + \alpha= \alpha + 1 + \alpha^2 + \alpha = \alpha^2+ 1\hspace{0.05cm}.$$
In this exercise you are to do some algebraic transformations in the Galois field $\rm GF(2^3)$ . Among other things you are asked for the multiplicative inverse of the element $\alpha^4$ . Then it must hold:
- $$\alpha^4 \cdot {\rm Inv_M}( \alpha^4) = 1 \hspace{0.05cm}.$$
Hints:
- This exercise belongs to the chapter "extension field".
- This exercise is intended as a supplement to the slightly more difficult "Exercise 2.5" .
Questions
Solution
- $$\alpha^7 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha \cdot \alpha^6 = \alpha \cdot (\alpha^2 + 1) = \alpha^3 + \alpha = (\alpha + 1) + \alpha = 1 \hspace{0.05cm},$$
- $$\alpha^8 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha \cdot \alpha^7 = \alpha \cdot 1 = \alpha\hspace{0.05cm},$$
- $$\alpha^{13} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha^7 \cdot \alpha^6 = 1 \cdot \alpha^6 = \alpha^2 + 1\hspace{0.05cm}.$$
The table can therefore be continued modulo $7$. This means: All proposed solutions are correct.
(2) Correct is the proposed solution 2 because of.
- $\alpha^8 = \alpha$ according to subtask (1),
- $\alpha^6 = \alpha^2 + 1$ (according to table), and
- $-\alpha^2 = \alpha^2$ (operations in the binary Galois field).
So applies:
- $$A = \alpha^8 + \alpha^6 - \alpha^2 + 1 = \alpha + (\alpha^2 + 1) + \alpha^2 + 1 = \alpha \hspace{0.05cm}.$$
(3) With $\alpha^{16} = \alpha^{16-14} = \alpha^2$ sowie $\alpha^{12} \cdot \alpha^3 = \alpha^{15} = \alpha^{15-14} = \alpha$ we obtain the proposed solution 5:
- $$B = \alpha^2 + \alpha= \alpha^4 \hspace{0.05cm}.$$
(4) It holds $\alpha^3 = \alpha + 1$ und damit $C = \alpha^3 + \alpha = \alpha + 1 + \alpha = 1$ ⇒ Proposed solution 1.
(5) With $\alpha^4 = \alpha^2 + \alpha$ we obtain $D = \alpha^4 + \alpha = \alpha^2$ ⇒ Proposed solution 3.
(6) Correct is the proposed solution 4:
- $$E = A \cdot B \cdot C/D = \alpha \cdot \alpha^4 \cdot 1/\alpha^2 = \alpha^3 \hspace{0.05cm}.$$
(7) According to the table, $\alpha^2 + \alpha = \alpha^4$ holds. Therefore must be valid:
- $$\alpha^4 \cdot {\rm Inv_M}( \alpha^4) = 1 \hspace{0.3cm} \Rightarrow\hspace{0.3cm} {\rm Inv_M}( \alpha^2 + \alpha) = {\rm Inv_M}( \alpha^4) = \alpha^{-4} = \alpha^3 \hspace{0.05cm}.$$
Because of $\alpha^3 = \alpha + 1$ the proposed solutions 2 and 3 are correct.