Difference between revisions of "Aufgaben:Exercise 3.09Z: Viterbi Algorithm again"
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Channel_Coding/Decoding_of_Convolutional_Codes}} |
| − | [[File:P_ID2656__KC_Z_3_8_neu.png|right|frame|Trellis | + | [[File:P_ID2656__KC_Z_3_8_neu.png|right|frame|Trellis for a rate 1/2 code, memory $m = 1$]] |
| − | + | The diagram shows the trellis of the convolutional code according to [[Aufgaben:Exercise_3.6:_State_Transition_Diagram| "Exercise 3.6"]], characterized by the following quantities: | |
| − | * Rate 1/2 ⇒ $k = 1, \ n = 2$, | + | * Rate 1/2 ⇒ $k = 1, \ n = 2$, |
| − | * | + | * memory $m = 1$, |
| − | * | + | * transfer function matrix $\mathbf{G}(D) = (1, \ 1 + D)$, |
| − | * | + | * length of information sequence: $L = 4$, |
| − | * | + | * sequence length including termination: $L\hspace{0.05cm}' = L + m = 5$. |
| − | + | On the basis of this representation, the Viterbi decoding is to be understood step by step, starting from the following reception sequence: $\underline{y} = (11, \, 01, \, 01, \, 11, \, 01)$. | |
| − | + | Drawn into the trellis are: | |
| − | * | + | * The initial value ${\it \Gamma}_0(S_0)$ for the Viterbi–algorithm, which is always chosen to $0$ . |
| − | * | + | * The two branch metrics for the first decoding step $(i = 1)$ are obtained with $\underline{y}_1 = (11)$ as follows: |
:$${\it \Gamma}_1(S_0) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\it \Gamma}_0(S_0) + d_{\rm H} \big ((00)\hspace{0.05cm},\hspace{0.05cm} (11) \big ) = 2 \hspace{0.05cm},$$ | :$${\it \Gamma}_1(S_0) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\it \Gamma}_0(S_0) + d_{\rm H} \big ((00)\hspace{0.05cm},\hspace{0.05cm} (11) \big ) = 2 \hspace{0.05cm},$$ | ||
:$${\it \Gamma}_1(S_1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\it \Gamma}_0(S_0) + d_{\rm H} \big ((11)\hspace{0.05cm},\hspace{0.05cm} (11) \big ) = 0 \hspace{0.05cm}.$$ | :$${\it \Gamma}_1(S_1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\it \Gamma}_0(S_0) + d_{\rm H} \big ((11)\hspace{0.05cm},\hspace{0.05cm} (11) \big ) = 0 \hspace{0.05cm}.$$ | ||
| − | * | + | * The branch metrics to step $i = 2$ ⇒ $\underline{y}_2 = (01)$ are obtained by the following comparisons: |
:$${\it \Gamma}_2(S_0) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}{\rm min} \left [{\it \Gamma}_{1}(S_0) + d_{\rm H} \big ((00)\hspace{0.05cm},\hspace{0.05cm} (01) \big )\hspace{0.05cm}, \hspace{0.2cm}{\it \Gamma}_{1}(S_1) + d_{\rm H} \big ((01)\hspace{0.05cm},\hspace{0.05cm} (01) \big ) \right ] $$ | :$${\it \Gamma}_2(S_0) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}{\rm min} \left [{\it \Gamma}_{1}(S_0) + d_{\rm H} \big ((00)\hspace{0.05cm},\hspace{0.05cm} (01) \big )\hspace{0.05cm}, \hspace{0.2cm}{\it \Gamma}_{1}(S_1) + d_{\rm H} \big ((01)\hspace{0.05cm},\hspace{0.05cm} (01) \big ) \right ] $$ | ||
:$$\Rightarrow\hspace{0.3cm} {\it \Gamma}_2(S_0) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm min} \big [ 2+1\hspace{0.05cm},\hspace{0.05cm} 0+0 \big ] = 0\hspace{0.05cm},$$ | :$$\Rightarrow\hspace{0.3cm} {\it \Gamma}_2(S_0) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm min} \big [ 2+1\hspace{0.05cm},\hspace{0.05cm} 0+0 \big ] = 0\hspace{0.05cm},$$ | ||
| Line 25: | Line 25: | ||
| − | In | + | In the same way you are to |
| − | * | + | * compute the branch metrics at time points $i = 3, \ i = 4$ and $i = 5$ (termination), and |
| − | * | + | * eliminate the less favorable paths to a node ${\it \Gamma}_i(S_{\mu})$ in each case. In the graph this is indicated by dotted lines for $i = 2$ . |
| − | + | Then the continuous path from ${\it \Gamma}_0(S_0)$ to ${\it \Gamma}_5(S_0)$ is to be found, where the backward direction is recommended. | |
| − | + | If one follows the found path in forward direction, one recognizes. | |
| − | * | + | * the most likely code sequence $\underline{z}$ $($ideally equal $\underline{x})$ by the labels, |
| − | * | + | * the most probable information sequence $\underline{v}$ $($ideally equal $\underline{u})$ at the colors. |
| Line 43: | Line 43: | ||
| − | + | Hints: | |
| − | * | + | * This exercise belongs to the chapter [[Channel_Coding/Decoding_of_Convolutional_Codes| "Decoding of Convolutional Codes"]]. |
| Line 50: | Line 50: | ||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Calculate the minimum branch metrics for time $i = 3$. |
|type="{}"} | |type="{}"} | ||
${\it \Gamma}_3(S_0) \ = \ ${ 1 } | ${\it \Gamma}_3(S_0) \ = \ ${ 1 } | ||
${\it \Gamma}_3(S_1) \ = \ ${ 1 } | ${\it \Gamma}_3(S_1) \ = \ ${ 1 } | ||
| − | { | + | {Calculate the minimum branch metrics for time $i = 4$. |
|type="{}"} | |type="{}"} | ||
${\it \Gamma}_4(S_0) \ = \ ${ 2 } | ${\it \Gamma}_4(S_0) \ = \ ${ 2 } | ||
${\it \Gamma}_4(S_1) \ = \ ${ 1 } | ${\it \Gamma}_4(S_1) \ = \ ${ 1 } | ||
| − | { | + | {Calculate the minimum branch metrics for time $i = 5$ (end). |
|type="{}"} | |type="{}"} | ||
${\it \Gamma}_5(S_0) \ = \ ${ 1 } | ${\it \Gamma}_5(S_0) \ = \ ${ 1 } | ||
| − | { | + | {What are the final results of the Viterbi algorithm: |
|type="[]"} | |type="[]"} | ||
+ $\underline{z} = (11, \, 01, \, 00, \, 11, \, 01)$. | + $\underline{z} = (11, \, 01, \, 00, \, 11, \, 01)$. | ||
| Line 73: | Line 73: | ||
- $\underline{v} = (1, \, 0, \, 1, \, 0, \, 0)$. | - $\underline{v} = (1, \, 0, \, 1, \, 0, \, 0)$. | ||
| − | { | + | {What decision would have been made without scheduling? |
|type="()"} | |type="()"} | ||
| − | + | + | + The same, |
| − | - | + | - another. |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
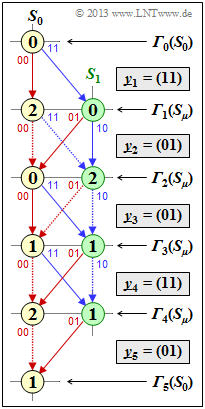
| − | '''(1)''' [[File:P_ID2657__KC_Z_3_8a_v1.png|right|frame|Trellis | + | '''(1)''' [[File:P_ID2657__KC_Z_3_8a_v1.png|right|frame|Trellis with branch metrics]] Starting from ${\it \Gamma}_2(S_0) = 0, \ {\it \Gamma}_2(S_1) = 2$ we get $\underline{y}_3 = (01)$: |
:$${\it \Gamma}_3(S_0) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm min} \left [0 + d_{\rm H} \big ((00), (01) \big ), \hspace{0.05cm}2 + d_{\rm H} \big ((01), (01) \big ) \right ] = {\rm min} \left [ 0+1\hspace{0.05cm},\hspace{0.05cm} 2+0 \right ] \hspace{0.15cm}\underline{= 1}\hspace{0.05cm},$$ | :$${\it \Gamma}_3(S_0) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm min} \left [0 + d_{\rm H} \big ((00), (01) \big ), \hspace{0.05cm}2 + d_{\rm H} \big ((01), (01) \big ) \right ] = {\rm min} \left [ 0+1\hspace{0.05cm},\hspace{0.05cm} 2+0 \right ] \hspace{0.15cm}\underline{= 1}\hspace{0.05cm},$$ | ||
:$${\it \Gamma}_3(S_1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}{\rm min} \left [0 + d_{\rm H} \big ((11), (01) \big ), \hspace{0.05cm}2 + d_{\rm H} \big ((10), (01) \big ) \right ] {\rm min} \left [ 0+1\hspace{0.05cm},\hspace{0.05cm} 2+2 \right ] \hspace{0.15cm}\underline{= 1}\hspace{0.05cm}.$$ | :$${\it \Gamma}_3(S_1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}{\rm min} \left [0 + d_{\rm H} \big ((11), (01) \big ), \hspace{0.05cm}2 + d_{\rm H} \big ((10), (01) \big ) \right ] {\rm min} \left [ 0+1\hspace{0.05cm},\hspace{0.05cm} 2+2 \right ] \hspace{0.15cm}\underline{= 1}\hspace{0.05cm}.$$ | ||
| − | + | Thus, eliminated are the two subpaths that start from state $S_1$ at time $i = 2$ (i.e., at the third decoding step) ⇒ Dotted in the graph. | |
| − | '''(2)''' | + | '''(2)''' Analogous to subtask (1), we obtain with $y_4 = (11)$: |
:$${\it \Gamma}_4(S_0) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}{\rm min} \left [1 + d_{\rm H} \big ((00), (11) \big ), \hspace{0.05cm}1 + d_{\rm H} \big ((01), (11) \big ) \right ] = {\rm min} \left [ 1+2\hspace{0.05cm},\hspace{0.05cm} 1+1 \right ] \hspace{0.15cm}\underline{= 2}\hspace{0.05cm},$$ | :$${\it \Gamma}_4(S_0) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}{\rm min} \left [1 + d_{\rm H} \big ((00), (11) \big ), \hspace{0.05cm}1 + d_{\rm H} \big ((01), (11) \big ) \right ] = {\rm min} \left [ 1+2\hspace{0.05cm},\hspace{0.05cm} 1+1 \right ] \hspace{0.15cm}\underline{= 2}\hspace{0.05cm},$$ | ||
:$${\it \Gamma}_4(S_1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}{\rm min} \left [1 + d_{\rm H} \big ((11), (11) \big ), \hspace{0.05cm}1 + d_{\rm H} \big ((10), (11) \big ) \right ] ={\rm min} \left [ 1+0\hspace{0.05cm},\hspace{0.05cm} 1+1 \right ] \hspace{0.15cm}\underline{= 1}\hspace{0.05cm}$$ | :$${\it \Gamma}_4(S_1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}{\rm min} \left [1 + d_{\rm H} \big ((11), (11) \big ), \hspace{0.05cm}1 + d_{\rm H} \big ((10), (11) \big ) \right ] ={\rm min} \left [ 1+0\hspace{0.05cm},\hspace{0.05cm} 1+1 \right ] \hspace{0.15cm}\underline{= 1}\hspace{0.05cm}$$ | ||
| − | ⇒ | + | ⇒ Elimination in the fourth decoding step of the two subpaths $S_0 → S_0$ and $S_1 → S_1$. |
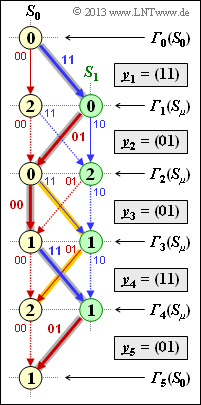
| − | [[File:P_ID2658__KC_Z_3_8d.png|right|frame| | + | [[File:P_ID2658__KC_Z_3_8d.png|right|frame|Path search]] |
| − | '''(3)''' Für $i = 5$ ⇒ " | + | '''(3)''' Für $i = 5$ ⇒ "Termination" is obtained with $\underline{y}_5 = (01)$: |
:$${\it \Gamma}_5(S_0) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}{\rm min} \left [2 + d_{\rm H} \big ((00), (01) \big ), \hspace{0.05cm}1 + d_{\rm H} \big ((01), (01) \big ) \right ] {\rm min} \left [ 2+1\hspace{0.05cm},\hspace{0.05cm} 1+0 \right ] \hspace{0.15cm}\underline{= 1}\hspace{0.05cm}.$$ | :$${\it \Gamma}_5(S_0) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}{\rm min} \left [2 + d_{\rm H} \big ((00), (01) \big ), \hspace{0.05cm}1 + d_{\rm H} \big ((01), (01) \big ) \right ] {\rm min} \left [ 2+1\hspace{0.05cm},\hspace{0.05cm} 1+0 \right ] \hspace{0.15cm}\underline{= 1}\hspace{0.05cm}.$$ | ||
| − | + | To be eliminated here is the subpath $S_0 → S_0$. | |
| − | '''(4)''' | + | '''(4)''' The backward search of the continuous path from ${\it \Gamma}_5(S_0)$ to ${\it \Gamma}_0(S_0)$ yields |
:$$S_0 ← S_1 ← S_0 ← S_0 ← S_1 ← S_0.$$ | :$$S_0 ← S_1 ← S_0 ← S_0 ← S_1 ← S_0.$$ | ||
| − | In | + | In the forward direction, this yields the path $S_0 → S_1 → S_0 → S_0 → S_1 → S_0$ and thus the |
| − | * | + | * the most likely code sequence $\underline{z} = (11, \, 01, \, 00, \, 11, \, 01)$, |
| − | * | + | * the most likely information sequence $\underline{v} = (1, \, 0, \, 0, \, 1, \, 0)$. |
| − | + | Thus, the <u>proposed solutions 1 and 3</u> are correct: | |
| − | * | + | *A comparison with the given received vector $\underline{y} = (11, \, 01, \, 01, \, 11, \, 01)$ shows that the sixth bit was corrupted during transmission. |
| − | '''(5)''' | + | '''(5)''' Without termination ⇒ final decision at $i = 4$, there would have been two continuous paths: |
| − | * | + | * from $S_0 → S_1 → S_0 → S_1 → S_0$ (shown in yellow), |
| − | * | + | * from $S_0 → S_1 → S_0 → S_0 → S_1$ (the ultimately correct path). |
| − | + | The constraint decision at time $i = 4$ would have led here to the second path and thus to the result $\underline{v} = (1, \, 0, \, 0, \, 1)$ because of ${\it \Gamma}_4(S_1) < {\it \Gamma}_4(S_0)$. | |
| − | * | + | *In the considered example, therefore, to the <u>same decision</u> as in subtask (4) with termination bit. |
| − | * | + | *However, there are many constellations where only the termination bit enables the correct and safe decision. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Revision as of 20:04, 18 October 2022
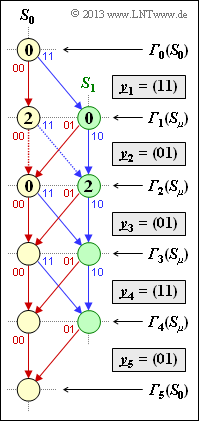
The diagram shows the trellis of the convolutional code according to "Exercise 3.6", characterized by the following quantities:
- Rate 1/2 ⇒ $k = 1, \ n = 2$,
- memory $m = 1$,
- transfer function matrix $\mathbf{G}(D) = (1, \ 1 + D)$,
- length of information sequence: $L = 4$,
- sequence length including termination: $L\hspace{0.05cm}' = L + m = 5$.
On the basis of this representation, the Viterbi decoding is to be understood step by step, starting from the following reception sequence: $\underline{y} = (11, \, 01, \, 01, \, 11, \, 01)$.
Drawn into the trellis are:
- The initial value ${\it \Gamma}_0(S_0)$ for the Viterbi–algorithm, which is always chosen to $0$ .
- The two branch metrics for the first decoding step $(i = 1)$ are obtained with $\underline{y}_1 = (11)$ as follows:
- $${\it \Gamma}_1(S_0) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\it \Gamma}_0(S_0) + d_{\rm H} \big ((00)\hspace{0.05cm},\hspace{0.05cm} (11) \big ) = 2 \hspace{0.05cm},$$
- $${\it \Gamma}_1(S_1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\it \Gamma}_0(S_0) + d_{\rm H} \big ((11)\hspace{0.05cm},\hspace{0.05cm} (11) \big ) = 0 \hspace{0.05cm}.$$
- The branch metrics to step $i = 2$ ⇒ $\underline{y}_2 = (01)$ are obtained by the following comparisons:
- $${\it \Gamma}_2(S_0) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}{\rm min} \left [{\it \Gamma}_{1}(S_0) + d_{\rm H} \big ((00)\hspace{0.05cm},\hspace{0.05cm} (01) \big )\hspace{0.05cm}, \hspace{0.2cm}{\it \Gamma}_{1}(S_1) + d_{\rm H} \big ((01)\hspace{0.05cm},\hspace{0.05cm} (01) \big ) \right ] $$
- $$\Rightarrow\hspace{0.3cm} {\it \Gamma}_2(S_0) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm min} \big [ 2+1\hspace{0.05cm},\hspace{0.05cm} 0+0 \big ] = 0\hspace{0.05cm},$$
- $${\it \Gamma}_2(S_1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}{\rm min} \left [{\it \Gamma}_{1}(S_0) + d_{\rm H} \big ((11)\hspace{0.05cm},\hspace{0.05cm} (01) \big )\hspace{0.05cm}, \hspace{0.2cm}{\it \Gamma}_{1}(S_1) + d_{\rm H} \big ((10)\hspace{0.05cm},\hspace{0.05cm} (01) \big ) \right ]$$
- $$\Rightarrow\hspace{0.3cm} {\it \Gamma}_2(S_1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm min} \big [ 2+1\hspace{0.05cm},\hspace{0.05cm} 0+2 \big ] = 2\hspace{0.05cm}.$$
In the same way you are to
- compute the branch metrics at time points $i = 3, \ i = 4$ and $i = 5$ (termination), and
- eliminate the less favorable paths to a node ${\it \Gamma}_i(S_{\mu})$ in each case. In the graph this is indicated by dotted lines for $i = 2$ .
Then the continuous path from ${\it \Gamma}_0(S_0)$ to ${\it \Gamma}_5(S_0)$ is to be found, where the backward direction is recommended.
If one follows the found path in forward direction, one recognizes.
- the most likely code sequence $\underline{z}$ $($ideally equal $\underline{x})$ by the labels,
- the most probable information sequence $\underline{v}$ $($ideally equal $\underline{u})$ at the colors.
Hints:
- This exercise belongs to the chapter "Decoding of Convolutional Codes".
Questions
Solution
- $${\it \Gamma}_3(S_0) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm min} \left [0 + d_{\rm H} \big ((00), (01) \big ), \hspace{0.05cm}2 + d_{\rm H} \big ((01), (01) \big ) \right ] = {\rm min} \left [ 0+1\hspace{0.05cm},\hspace{0.05cm} 2+0 \right ] \hspace{0.15cm}\underline{= 1}\hspace{0.05cm},$$
- $${\it \Gamma}_3(S_1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}{\rm min} \left [0 + d_{\rm H} \big ((11), (01) \big ), \hspace{0.05cm}2 + d_{\rm H} \big ((10), (01) \big ) \right ] {\rm min} \left [ 0+1\hspace{0.05cm},\hspace{0.05cm} 2+2 \right ] \hspace{0.15cm}\underline{= 1}\hspace{0.05cm}.$$
Thus, eliminated are the two subpaths that start from state $S_1$ at time $i = 2$ (i.e., at the third decoding step) ⇒ Dotted in the graph.
(2) Analogous to subtask (1), we obtain with $y_4 = (11)$:
- $${\it \Gamma}_4(S_0) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}{\rm min} \left [1 + d_{\rm H} \big ((00), (11) \big ), \hspace{0.05cm}1 + d_{\rm H} \big ((01), (11) \big ) \right ] = {\rm min} \left [ 1+2\hspace{0.05cm},\hspace{0.05cm} 1+1 \right ] \hspace{0.15cm}\underline{= 2}\hspace{0.05cm},$$
- $${\it \Gamma}_4(S_1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}{\rm min} \left [1 + d_{\rm H} \big ((11), (11) \big ), \hspace{0.05cm}1 + d_{\rm H} \big ((10), (11) \big ) \right ] ={\rm min} \left [ 1+0\hspace{0.05cm},\hspace{0.05cm} 1+1 \right ] \hspace{0.15cm}\underline{= 1}\hspace{0.05cm}$$
⇒ Elimination in the fourth decoding step of the two subpaths $S_0 → S_0$ and $S_1 → S_1$.
(3) Für $i = 5$ ⇒ "Termination" is obtained with $\underline{y}_5 = (01)$:
- $${\it \Gamma}_5(S_0) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}{\rm min} \left [2 + d_{\rm H} \big ((00), (01) \big ), \hspace{0.05cm}1 + d_{\rm H} \big ((01), (01) \big ) \right ] {\rm min} \left [ 2+1\hspace{0.05cm},\hspace{0.05cm} 1+0 \right ] \hspace{0.15cm}\underline{= 1}\hspace{0.05cm}.$$
To be eliminated here is the subpath $S_0 → S_0$.
(4) The backward search of the continuous path from ${\it \Gamma}_5(S_0)$ to ${\it \Gamma}_0(S_0)$ yields
- $$S_0 ← S_1 ← S_0 ← S_0 ← S_1 ← S_0.$$
In the forward direction, this yields the path $S_0 → S_1 → S_0 → S_0 → S_1 → S_0$ and thus the
- the most likely code sequence $\underline{z} = (11, \, 01, \, 00, \, 11, \, 01)$,
- the most likely information sequence $\underline{v} = (1, \, 0, \, 0, \, 1, \, 0)$.
Thus, the proposed solutions 1 and 3 are correct:
- A comparison with the given received vector $\underline{y} = (11, \, 01, \, 01, \, 11, \, 01)$ shows that the sixth bit was corrupted during transmission.
(5) Without termination ⇒ final decision at $i = 4$, there would have been two continuous paths:
- from $S_0 → S_1 → S_0 → S_1 → S_0$ (shown in yellow),
- from $S_0 → S_1 → S_0 → S_0 → S_1$ (the ultimately correct path).
The constraint decision at time $i = 4$ would have led here to the second path and thus to the result $\underline{v} = (1, \, 0, \, 0, \, 1)$ because of ${\it \Gamma}_4(S_1) < {\it \Gamma}_4(S_0)$.
- In the considered example, therefore, to the same decision as in subtask (4) with termination bit.
- However, there are many constellations where only the termination bit enables the correct and safe decision.