Difference between revisions of "Aufgaben:Exercise 4.11: Analysis of Parity-check Matrices"
m (Guenter moved page Aufgabe 4.11: Analyse von Prüfmatrizen to Exercise 4.11: Analysis of Parity-Check Matrices) |
m (Guenter moved page Exercise 4.11: Analysis of Parity-Check Matrices to Exercise 4.11: Analysis of Parity-check Matrices) |
(No difference)
| |
Revision as of 14:02, 22 November 2022
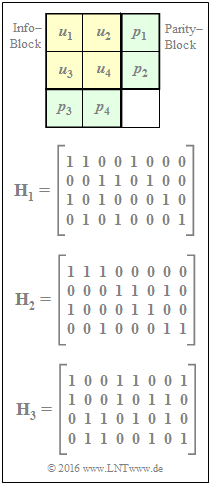
In nebenstehender Grafik ist oben ein Produktcode angegeben, der durch folgende Prüfgleichungen gekennzeichnet ist:
- $$p_1 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_1 \oplus u_2\hspace{0.05cm},\hspace{0.3cm} p_2 = u_3 \oplus u_4\hspace{0.05cm},\hspace{0.3cm} p_3 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_1 \oplus u_3\hspace{0.05cm},\hspace{0.3cm} p_4 = u_2 \oplus u_4\hspace{0.05cm}.$$
Darunter sind die Prüfmatrizen $\mathbf{H}_1, \ \mathbf{H}_2$ und $\mathbf{H}_3$ angegeben. Zu prüfen ist, welche der Matrizen den gegebenen Produktcode entsprechend der Gleichung $\underline{x} = \underline{u} \cdot \mathbf{H}^{\rm T}$ richtig beschreiben, wenn von folgenden Definitionen ausgegangen wird:
- dem Codewort $\underline{x} = (u_1, \, u_2, \, u_3, \, u_4, \, p_1, \, p_2, \, p_3, \, p_4)$,
- dem Codewort $\underline{x} = (u_1, \, p_1, \, u_2, \, p_2, \, u_3, \, p_3, \, u_4, \, p_4)$.
Alle $\mathbf{H}$–Matrizen beinhalten weniger Einsen als Nullen. Dies ist ein Kennzeichen der so genannten Low–density Parity–check Codes (kurz: $\rm LDPC$–Codes). Bei den praxisrelevanten LDPC–Codes ist der Einsen–Anteil allerdings noch deutlich geringer als bei diesen Beispielen.
Weiterhin ist für die Aufgabe anzumerken:
- Ein $(n, \ k)$–Blockcode ist systematisch, wenn die ersten $k$ Bit des Codewortes $\underline{x}$ das Informationswort $\underline{u}$ beinhaltet. Mit der Codewortdefinition $\underline{x} = (u_1, \, u_2, \, u_3, \, u_4, \, p_1, \, p_2, \, p_3, \, p_4)$ muss dann die Prüfmatrix $\mathbf{H}$ mit einer $k × k$–Diagonalmatrix enden.
- Ein regulärer Code (hinsichtlich LDPC–Anwendung) liegt vor, wenn das Hamming–Gewicht aller Zeilen ⇒ $w_{\rm Z}$ und das Hamming–Gewicht aller Spalten ⇒ $w_{\rm S}$ jeweils gleich sind. Andernfalls spricht man von einem irregulären LDPC–Code.
- Die Prüfmatrix $\mathbf{H}$ eines herkömmlichen linearen $(n, \ k)$–Blockcodes besteht aus exakt $m = n - k$ Zeilen und $n$ Spalten. Bei den LDPC–Codes lautet dagegen die Forderung: $m ≥ n - k$. Das Gleichheitszeichen trifft dann zu, wenn die $m$ Prüfgleichungen statistisch unabhängig sind.
- Aus der Prüfmatrix $\mathbf{H}$ lässt sich eine untere Schranke für die Coderate $R$ angeben:
- $$R \ge 1 - \frac{{\rm E}[w_{\rm S}]}{{\rm E}[w_{\rm Z}]} \hspace{0.5cm}{\rm mit}\hspace{0.5cm} {\rm E}[w_{\rm S}] =\frac{1}{n} \cdot \sum_{i = 1}^{n}w_{\rm S}(i) \hspace{0.5cm}{\rm und}\hspace{0.5cm} {\rm E}[w_{\rm Z}] =\frac{1}{m} \cdot \sum_{j = 1}^{ m}w_{\rm Z}(j) \hspace{0.05cm}.$$
- Diese Gleichung gilt für reguläre und irreguläre LDPC–Codes gleichermaßen, wobei den regulären Codes ${\rm E}[w_{\rm S}] = w_{\rm S}$ und ${\rm E}[w_{\rm Z}] = w_{\rm Z}$ berücksichtigt werden kann.
Hinweise:
- Die Aufgabe gehört zum Kapitel Grundlegendes zu den Low–density Parity–check.
- Bezug genommen wird insbesondere auf die Seite Einige Charakteristika der LDPC–Codes.
Fragebogen
Musterlösung
- Mit der Codewortdefinition $\underline{x} = (u_1, \, u_2, \, u_3, \, u_4, \, p_1, \, p_2, \, p_3, \, p_4)$ bezeichnet die Prüfmatrix $\mathbf{H}_1$ folgende Prüfgleichungen:
- $$u_1 \oplus u_2 \oplus p_1 = 0\hspace{0.05cm},\hspace{0.3cm} u_3 \oplus u_4 \oplus p_2 = 0\hspace{0.05cm},\hspace{0.3cm} u_1 \oplus u_3 \oplus p_3 = 0\hspace{0.05cm},\hspace{0.3cm} u_2 \oplus u_4 \oplus p_4 = 0\hspace{0.05cm}.$$
- Dies entspricht genau den vorne getroffenen Annahmen. Das gleiche Ergebnis erhält man für $\mathbf{H}_2$ und der Codewortdefinition $\underline{x} = (u_1, \, p_1, \, u_2, \, p_2, \, u_3, \, p_3, \, u_4, \, p_4)$.
Bei gleicher Codewortdefinition $\underline{x} = (u_1, \, p_1, \, u_2, \, p_2, \, u_3, \, p_3, \, u_4, \, p_4)$ liefern die anderen Prüfmatrizen keinen sinnvollen Gleichungssatz:
- Entsprechend Prüfmatrix $\mathbf{H}_1$:
- $$u_1 \oplus p_1 \oplus u_3 = 0\hspace{0.05cm},\hspace{0.3cm} u_2 \oplus p_2 \oplus p_3 = 0\hspace{0.05cm},\hspace{0.3cm} u_1 \oplus u_2 \oplus u_4 = 0\hspace{0.05cm},\hspace{0.3cm} p_1 \oplus p_2 \oplus p_4 = 0\hspace{0.05cm};$$
- entsprechend Prüfmatrix $\mathbf{H}_3$:
- $$u_1 \hspace{-0.12cm}\oplus\hspace{-0.06cm} p_2 \hspace{-0.12cm}\oplus\hspace{-0.06cm} u_3 \hspace{-0.12cm}\oplus\hspace{-0.06cm} p_4 \hspace{-0.05cm} = \hspace{-0.05cm} 0\hspace{0.05cm},\hspace{0.15cm} u_1 \hspace{-0.12cm}\oplus\hspace{-0.06cm} p_2 \hspace{-0.12cm}\oplus\hspace{-0.06cm} p_3 \hspace{-0.12cm}\oplus\hspace{-0.06cm}u_4 \hspace{-0.05cm} = \hspace{-0.05cm} 0\hspace{0.05cm},\hspace{0.15cm} p_1 \hspace{-0.12cm}\oplus\hspace{-0.06cm} u_2 \hspace{-0.12cm}\oplus\hspace{-0.06cm} u_3 \hspace{-0.12cm}\oplus\hspace{-0.06cm}u_4 \hspace{-0.05cm} = \hspace{-0.05cm} 0\hspace{0.05cm},\hspace{0.15cm} p_1 \hspace{-0.12cm}\oplus\hspace{-0.06cm} u_2 \hspace{-0.12cm}\oplus\hspace{-0.06cm} p_3 \hspace{-0.12cm}\oplus\hspace{-0.06cm} p_4 \hspace{-0.05cm} = \hspace{-0.05cm} 0\hspace{0.05cm}.$$
(2) Richtig sind die Lösungsvorschläge 1 und 4:
- Der Code ist systematisch, weil $\mathbf{H}_1$ mit einer $4 × 4$–Diagonalmatrix endet.
- Bei einem regulären (LDPC)–Code müssten in jeder Zeile und in jeder Spalte gleich viele Einsen sein.
- Die erste Bedingung ist erfüllt $(w_{\rm Z} = 3)$, nicht aber die zweite. Vielmehr gibt es (gleich oft) eine Eins bzw. zwei Einsen pro Spalte ⇒ ${\rm E}[w_{\rm S}] = 1.5$.
- Bei einem irregulären Code lautet die untere Schranke für die Coderate:
- $$R \ge 1 - \frac{{\rm E}[w_{\rm S}]}{{\rm E}[w_{\rm Z}]} = 1 - \frac{1.5}{3} = 1/2 \hspace{0.05cm}.$$
- Wegen der gegebenen Codestruktur ($k = 4$ Informationsbits, $m = 4$ Prüfbits ⇒ $n = 8$ Codebits) ist hier die Coderate auch in der herkömmlichen Form angebbar: $R = k/n$ ⇒ Richtig ist Lösungsvorschlag 4 im Gegensatz zur Antwort 3.
(3) Die $\mathbf{H}_3$–Zeilen ergeben sich aus Linearkombinationen von $\mathbf{H}_1$–Zeilen:
- Die erste $\mathbf{H}_3$–Zeile ist die Summe von Zeile 1 und Zeile 4.
- Die zweite $\mathbf{H}_3$–Zeile ist die Summe von Zeile 2 und Zeile 3.
- Die dritte $\mathbf{H}_3$–Zeile ist die Summe von Zeile 1 und Zeile 3.
- Die vierte $\mathbf{H}_3$–Zeile ist die Summe von Zeile 2 und Zeile 4.
Durch Linearkombinationen werden aus den vier linear unabhängigen Gleichungen bezüglich $\mathbf{H}_1$ nun vier linear unabhängige Gleichungen bezüglich $\mathbf{H}_3$
⇒ Richtig sind also die Lösungsvorschläge 2 und 3.
(4) Hier sind die Lösungsvorschläge 2, 3 und 4 richtig:
- Wäre der durch $\mathbf{H}_3$ beschriebene Code systematisch, müsste $\mathbf{H}_3$ mit einer $4 × 4$–Diagonalmatrix enden. Dies ist hier nicht der Fall.
- Die Hamming–Gewichte aller Zeilen sind gleich $(w_{\rm Z} = 4)$ und auch alle Spalten haben jeweils das gleiche Hamming–Gewicht $(w_{\rm S} = 2)$ ⇒ der Code ist regulär.
- Daraus ergibt sich für die Coderate $R ≥ 1 - 2/4 = 1/2$. Da aber auch die vier Zeilen von $\mathbf{H}_3$ vier unabhängige Gleichungen beschreiben, gilt ebenfalls das Gleichheitszeichen ⇒ $R = 1/2$.