Aufgaben:Exercise 4.08Z: Basics about Interleaving

• Return to book

Interleaver description

Interleaving is required, for example, for a channel with burst error characteristics in order to distribute the errors within the burst over a sufficiently large area so that they can subsequently be largely corrected (or at least detected).

Für Turbocodes, die auf so genannten  RSC–Coder  (Recursive Systematic Convolutional Encoder)  basieren – und nur solche machen Sinn – ist Interleaving auch beim AWGN–Kanal essentiell, da es dann auch stets (einige) Eingangssequenzen gibt, die in der Ausgangsfolge nach etlichen Einsen nur noch Nullen liefern, und zwar bis ins Unendliche   ⇒   es gibt Ausgangsfolgen mit sehr kleinem Hamming–Gewicht.

Verteilt man im zweiten Coder die Bits solcher Eingangssequenzen über einen weiten Bereich, so kann bei iterativer symbolweiser Decodierung das Problem durch das Zusammenspiel beider Komponentendecoder (weitgehend) beseitigt werden.

Man unterscheidet allgemein zwischen

• Block–Interleaver und
• Random–Interleaver.

Bei Block–Interleaving  füllt man eine Matrix mit  $S$  Spalten und  $Z$  Zeilen spaltenweise und liest die Matrix zeilenweise aus. Damit wird ein Informationsblock mit  $I_{\rm max} = S \cdot Z$  Bit deterministisch verwürfelt.

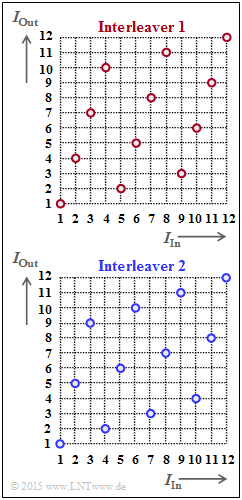
Rechts sind zwei Interleaver angegeben und zwar in grafischer Form durch die Zuordnung  $I_{\rm Out}(I_{\rm In})$. Diese Größen stehen für den "Index der Ausgangsfolge" bzw. für den "Index der Eingangsfolge". Es gilt:

$$1 \le I_{\rm Out} \le I_{\rm max} \hspace{0.05cm}, \hspace{0.5cm} 1 \le I_{\rm In} \le I_{\rm max} \hspace{0.05cm}. $$

In der Teilaufgabe  (1)  ist gefragt, ob es sich hierbei um  Block–Interleaving  oder um  Random Interleaving  handelt. Letztere werden im  Theorieteil  allerdings nur in aller Kürze besprochen.

Hinweis:

• Die Aufgabe bezieht sich auf das Kapitel  Grundlegendes zu den Turbocodes.

• Aber auch in anderen $\rm LNTwww$–Büchern wird Interleaving behandelt, unter anderem im Buch "Beispiele von Nachrichtensystemen" mit Bezug zum

• Standard  Digital Subscriber Line (DSL)   ⇒   Interleaving und De–Interleaving,
• 2G–Mobilfunksystem  GSM   ⇒   Komponenten der Sprach– und Datenübertragung,
• 3G–Mobilfunksystem  UMTS   ⇒   Kanalcodierung,
• 4G–Mobilfunksystem  LTE   ⇒   Funktionsweise von SC–FDMA  (im Buch "Mobile Kommunikation").

Fragebogen

1

Welche Interleaver–Art ist in der Grafik auf der Angabenseite dargestellt?

	Block–Interleaving,
	Random–Interleaving.

2

Wieviele Zeilen  ($Z$)  und Spalten  ($S$)  hat die obere "Interleaver–Matrix 1"?

$Z \ = \ $

$S \ = \ $

3

Es gelte  $\underline{u} = (1001'0001'1101'1101'0010'0111)$. Wie beginnt die verwürfelte Folge  $\underline{u}_{\pi}$?
    Hinweis:   Die Hochkommata dienen nur als Lesehilfe.

	$\underline{u}_{\pi} = (110'100'100'011'111'110'010'001' \text{...}\ )$,
	$\underline{u}_{\pi} = (101'001'000'111'100'101'011'101'\text{...}\ )$.

4

Die verwürfelte Folge sei  $\underline{u}_{\pi} = (100'100'011'101'110'100'100'111)$. Wie lautet die Folge nach dem De–Interleaving?

	$\underline{u} = (1101'0010'0011'1111'1001'0001'\text{...}\ )$,
	$\underline{u} = (1010'0100'0111'1001'0101'1101' \text{...}\ )$.

Musterlösung

Solution

4×3–Interleaver–Matrix

(1)  Aus der regelmäßigen Struktur der Funktion $I_{\rm Out}(I_{\rm In})$ erkennt man, dass es sich um einen Blockinterleaver handelt  ⇒  Antwort 1.

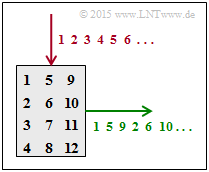
(2)  Der Index "1" wird als erstes Zeichen ausgegeben. Weiter gilt:

• Der Index 5 wird als zweites Zeichen ausgegeben  ⇒  $\underline{Z = 4}$.
• Der Index 2 wird als viertes Zeichen ausgegeben  ⇒  $\underline{S = 3}$.

Die obere Grafik zeigt für die 4×3–Interleaver–Matrix:

• das spaltenweise Beschreiben (rot),
• das zeilenweise Auslesen (grün).

Zum Interleaving

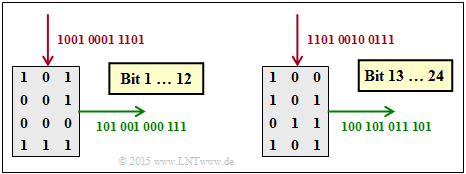
(3)  Richtig ist der der Lösungsvorschlag 2:

• Die Matrix wird spaltenweise beschrieben und zeilenweise ausgelesen.
• Nach 12 Bit wird die Matrix gelöscht und die Prozedur beginnt von Neuem.
• Die Grafik zeigt, dass nun der Lösungsvorschlag 2 richtig ist.

Zum De–Interleaving

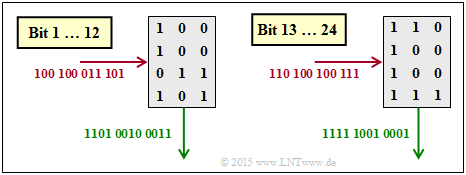
(4)  Richtig ist der der Lösungsvorschlag 1:

• Beim De–Interleaving wird die Matrix zeilenweise beschrieben und spaltenweise ausgelesen.
• Die Grafik zeigt, dass hier der Lösungsvorschlag 1 richtig ist.