Applets:Pulses and Spectra

Open Applet in new Tab   Deutsche Version Öffnen

Applet Description

Time-limited symmetric signals   ⇒   "pulses"  $x(t)$  and the corresponding spectral functions  $X(f)$  are considered, namely

• Gaussian pulse, 
• rectangular pulse,  
• triangular pulse, 
• trapezoidal pulse, 
• cosine roll-off pulse,
• cosine square pulse.

Further it is to be noted:

• The functions  $x(t)$  resp.  $X(f)$  are shown for up to two parameter sets in one diagram each.
• The red curves and numbers apply to the left parameter set, the blue ones to the right parameter set.
• The abscissas  $t$  (time) and  $f$  (frequency) as well as the ordinates  $x(t)$  (signal values) and  $X(f)$  (spectral values) are normalized.

Theoretical Background

Relationship $x(t)\Leftrightarrow X(f)$

• Der Zusammenhang zwischen der Zeitfunktion  $x(t)$  und dem Spektrum  $X(f)$  ist durch das  erste Fourierintegral  gegeben:

$$X(f)={\rm FT} [x(t)] = \int_{-\infty}^{+\infty}x(t)\cdot {\rm e}^{-{\rm j}2\pi f t}\hspace{0.15cm} {\rm d}t\hspace{1cm} \rm FT\hspace{-0.1cm}: \ Fouriertransformation.$$

• Um aus der Spektralfunktion  $X(f)$  die Zeitfunktion  $x(t)$  berechnen zu können, benötigt man das  zweite Fourierintegral:

$$x(t)={\rm IFT} [X(f)] = \int_{-\infty}^{+\infty}X(f)\cdot {\rm e}^{+{\rm j}2\pi f t}\hspace{0.15cm} {\rm d}f\hspace{1cm} {\rm IFT}\hspace{-0.1cm}: \rm Inverse \ Fouriertransformation.$$

• In allen Beispielen verwenden wir reelle und gerade Funktionen.  Somit gilt:

$$x(t)=\int_{-\infty}^{+\infty}X(f)\cdot \cos(2\pi ft) \hspace{0.15cm} {\rm d}f \ \ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\ \ \ X(f)=\int_{-\infty}^{+\infty}x(t)\cdot \cos(2\pi ft) \hspace{0.15cm} {\rm d}t .$$

• $x(t)$  und  $X(f)$  haben unterschiedliche Einheiten, beispielsweise  $x(t)$  in  $\rm V$,  $X(f)$  in  $\rm V/Hz$.
• Der Zusammenhang zwischen diesem Modul und dem ähnlich aufgebauten Applet  Frequenzgang & Impulsantwort  basiert auf dem  Vertauschungssatz.
• Alle Zeiten sind auf eine Zeit  $T$  normiert und alle Frequenzen auf  $1/T$   ⇒   die Spektralwerte  $X(f)$  müssen noch mit der Normierungszeit  $T$  multipliziert werden.

$\text{Beispiel:}$   Stellt man einen Rechteckimpuls mit Amplitude  $A_1 = 1$  und äquivalenter Impulsdauer  $\Delta t_1 = 1$  ein, so ist  $x_1(t)$  im Bereich  $-0.5 < t < +0.5$  gleich Eins und außerhalb dieses Bereichs gleich Null.  Die Spektralfunktion  $X_1(f)$  verläuft  $\rm si$–förmig mit  $X_1(f= 0) = 1$  und der ersten Nullstelle bei  $f=1$.

• Soll mit dieser Einstellung ein Rechteckimpuls mit  $A = K = 3 \ \rm V$  und  $\Delta t = T = 2 \ \rm ms$  nachgebildet werden, dann sind alle Signalwerte mit  $K = 3 \ \rm V$  und alle Spektralwerte mit  $K \cdot T = 0.006 \ \rm V/Hz$  zu multiplizieren.
• Der maximale Spektralwert ist dann  $X(f= 0) = 0.006 \ \rm V/Hz$  und die erste Nullstelle liegt bei  $f=1/T = 0.5 \ \rm kHz$.

Gaussian Pulse

• Die Zeitfunktion des Gaußimpulses mit der Höhe  $K$  und der (äquivalenten) Dauer  $\Delta t$  lautet:

$$x(t)=K\cdot {\rm e}^{-\pi\hspace{0.05cm}\cdot \hspace{0.05cm}(t/\Delta t)^2}.$$

• Die äquivalente Zeitdauer  $\Delta t$  ergibt sich aus dem flächengleichen Rechteck.
• Der Wert bei  $t = \Delta t/2$  ist um den Faktor  $0.456$  kleiner als der Wert bei  $t=0$.
• Für die Spektralfunktion erhält man gemäß der Fouriertransformation:

$$X(f)=K\cdot \Delta t \cdot {\rm e}^{-\pi(f\hspace{0.05cm}\cdot \hspace{0.05cm} \Delta t)^2} .$$

• Je kleiner die äquivalente Zeitdauer  $\Delta t$  ist, um so breiter und niedriger ist das Spektrum   ⇒   Reziprozitätsgesetz von Bandbreite und Impulsdauer.
• Sowohl  $x(t)$  als auch  $X(f)$  sind zu keinem  $f$–  bzw.  $t$–Wert exakt gleich Null.
• Für praktische Anwendungen kann der Gaußimpuls jedoch in Zeit und Frequenz als begrenzt angenommen werden.  Zum Beispiel ist  $x(t)$  bereits bei  $t=1.5 \Delta t$  auf weniger als  $0.1\%$  des Maximums abgefallen.

Rectangular Pulse

• Die Zeitfunktion des Rechteckimpulses mit der Höhe  $K$  und der (äquivalenten) Dauer  $\Delta t$  lautet:

$$x(t) = \left\{ \begin{array}{l} \hspace{0.25cm}K \\ K /2 \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.05cm} t\hspace{0.05cm} \right| < T/2,} \\ {\left| \hspace{0.05cm}t\hspace{0.05cm} \right| = T/2,} \\ {\left|\hspace{0.05cm} t \hspace{0.05cm} \right| > T/2.} \\ \end{array}$$

• Der  $\pm \Delta t/2$–Wert liegt mittig zwischen links- und rechtsseitigem Grenzwert.
• Für die Spektralfunktion erhält man entsprechend den Gesetzmäßigkeiten der Fouriertransformation (1. Fourierintegral):

$$X(f)=K\cdot \Delta t \cdot {\rm si}(\pi\cdot \Delta t \cdot f) \quad \text{mit} \ {\rm si}(x)=\frac{\sin(x)}{x}.$$

• Der Spektralwert bei  $f=0$  ist gleich der Rechteckfläche der Zeitfunktion.
• Die Spektralfunktion besitzt Nullstellen in äquidistanten Abständen  $1/\Delta t$.
• Das Integral über der Spektralfunktion  $X(f)$  ist gleich dem Signalwert zum Zeitpunkt  $t=0$, also der Impulshöhe  $K$.

Triangular Pulse

• Die Zeitfunktion des Dreieckimpulses mit der Höhe  $K$  und der (äquivalenten) Dauer  $\Delta t$  lautet:

$$x(t) = \left\{ \begin{array}{l} \hspace{0.25cm}K\cdot (1-|t|/{\Delta t}) \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.05cm} t\hspace{0.05cm} \right| < \Delta t,} \\ {\left| \hspace{0.05cm}t\hspace{0.05cm} \right| \ge \Delta t.} \\ \end{array}$$

• Die absolute Zeitdauer ist  $2 \cdot \Delta t$;  diese ist doppelt so groß als die des Rechtecks.
• Für die Spektralfunktion erhält man gemäß der Fouriertransformation:

$$X(f)=K\cdot \Delta f \cdot {\rm si}^2(\pi\cdot \Delta t \cdot f) \quad \text{mit} \quad {\rm si}(x)=\frac{\sin(x)}{x}.$$

• Obige Zeitfunktion ist gleich der Faltung zweier Rechteckimpulse, jeweils mit Breite  $\Delta t$.
• Daraus folgt:  $X(f)$  beinhaltet anstelle der  ${\rm si}$-Funktion die  ${\rm si}^2$-Funktion.
• $X(f)$  weist somit ebenfalls Nullstellen im äquidistanten Abständen  $1/\Delta f$  auf.
• Der asymptotische Abfall von  $X(f)$  erfolgt hier mit  $1/f^2$, während zum Vergleich der Rechteckimpuls mit  $1/f$  abfällt.

Trapezoidal Pulse

Die Zeitfunktion des Trapezimpulses mit der Höhe  $K$  und den Zeitparametern  $t_1$  und  $t_2$  lautet:

$$x(t) = \left\{ \begin{array}{l} \hspace{0.25cm}K \\ K\cdot \frac{t_2-|t|}{t_2-t_1} \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{20}c} {\rm{f\ddot{u}r}}\quad \\ {\rm{f\ddot{u}r}}\quad \\ {\rm{f\ddot{u}r}} \quad \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.05cm} t\hspace{0.05cm} \right| \le t_1,} \\ {t_1\le \left| \hspace{0.05cm}t\hspace{0.05cm} \right| \le t_2,} \\ {\left|\hspace{0.05cm} t \hspace{0.05cm} \right| \ge t_2.} \\ \end{array}$$

• Für die äquivalente Impulsdauer (flächengleiches Rechteck) gilt:   $\Delta t = t_1+t_2$.
• Der Rolloff-Faktor (im Zeitbereich) kennzeichnet die Flankensteilheit:

$$r=\frac{t_2-t_1}{t_2+t_1}.$$

• Der Sonderfall  $r=0$  entspricht dem Rechteckimpuls und der Sonderfall  $r=1$  dem Dreieckimpuls.
• Für die Spektralfunktion erhält man gemäß der Fouriertransformation:

$$X(f)=K\cdot \Delta t \cdot {\rm si}(\pi\cdot \Delta t \cdot f)\cdot {\rm si}(\pi \cdot r \cdot \Delta t \cdot f) \quad \text{mit} \quad {\rm si}(x)=\frac{\sin(x)}{x}.$$

• Der asymptotische Abfall von  $X(f)$  liegt zwischen  $1/f$  $($für Rechteck,  $r=0)$  und  $1/f^2$  $($für Dreieck,  $r=1)$.

Cosine roll-off Pulse

Die Zeitfunktion des Cosinus-Rolloff-Impulses mit der Höhe  $K$  und den Zeitparametern  $t_1$  und  $t_2$  lautet:

$$x(t) = \left\{ \begin{array}{l} \hspace{0.25cm}K \\ K\cdot \cos^2\Big(\frac{|t|-t_1}{t_2-t_1}\cdot {\pi}/{2}\Big) \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{20}c} {\rm{f\ddot{u}r}}\quad \\ {\rm{f\ddot{u}r}}\quad \\ {\rm{f\ddot{u}r}}\quad \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.05cm} t\hspace{0.05cm} \right| \le t_1,} \\ {t_1\le \left| \hspace{0.05cm}t\hspace{0.05cm} \right| \le t_2,} \\ {\left|\hspace{0.05cm} t \hspace{0.05cm} \right| \ge t_2.} \\ \end{array}$$

• Für die äquivalente Impulsdauer (flächengleiches Rechteck) gilt:   $\Delta t = t_1+t_2$.
• Der Rolloff-Faktor (im Zeitbereich) kennzeichnet die Flankensteilheit:

$$r=\frac{t_2-t_1}{t_2+t_1}.$$

• Der Sonderfall  $r=0$  entspricht dem Rechteckimpuls und der Sonderfall  $r=1$  dem Cosinus-Quadrat-Impuls.
• Für die Spektralfunktion erhält man gemäß der Fouriertransformation:

$$X(f)=K\cdot \Delta t \cdot \frac{\cos(\pi \cdot r\cdot \Delta t \cdot f)}{1-(2\cdot r\cdot \Delta t \cdot f)^2} \cdot {\rm si}(\pi \cdot \Delta t \cdot f).$$

• Je größer der Rolloff-Faktor  $r$  ist, desto schneller nimmt  $X(f)$  asymptotisch mit  $f$  ab.

Cosine square Pulse

• Dies ist ein Sonderfall des Cosinus-Rolloff-Impulses und ergibt sich für  $r=1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}t_1=0, \ t_2= \Delta t$:

$$x(t) = \left\{ \begin{array}{l} \hspace{0.25cm}K\cdot \cos^2\Big(\frac{|t|\hspace{0.05cm}\cdot \hspace{0.05cm} \pi}{2\hspace{0.05cm}\cdot \hspace{0.05cm} \Delta t}\Big) \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.05cm} t\hspace{0.05cm} \right| < \Delta t,} \\ {\left| \hspace{0.05cm}t\hspace{0.05cm} \right| \ge \Delta t.} \\ \end{array}$$

• Für die Spektralfunktion erhält man gemäß der Fouriertransformation:

$$X(f)=K\cdot \Delta f \cdot \frac{\pi}{4}\cdot \big [{\rm si}(\pi(\Delta t\cdot f +0.5))+{\rm si}(\pi(\Delta t\cdot f -0.5))\big ]\cdot {\rm si}(\pi \cdot \Delta t \cdot f).$$

• Wegen der letzten  ${\rm si}$-Funktion ist  $X(f)=0$  für alle Vielfachen von  $F=1/\Delta t$.  Die äquidistanten Nulldurchgänge des Cos-Rolloff-Impulses bleiben erhalten.
• Aufgrund des Klammerausdrucks weist  $X(f)$  nun weitere Nulldurchgänge bei  $f=\pm1.5 F$,  $\pm2.5 F$,  $\pm3.5 F$, ... auf.
• Für die Frequenz  $f=\pm F/2$  erhält man die Spektralwerte  $K\cdot \Delta t/2$.
• Der asymptotische Abfall von  $X(f)$  verläuft in diesem Sonderfall mit  $1/f^3$.

Exercises

• First select the number  $(1,\text{...}, 7)$  of the exercise.  The number  $0$  corresponds to a "Reset":  Same setting as at program start.
• A task description is displayed.  The parameter values ​​are adjusted.  Solution after pressing "Show solution".
  
• "Red" refers to the first parameter set ⇒ $x_1(t) \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\ X_1(f)$,  "Blue" refers to the second parameter set ⇒ $x_2(t) \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\ X_2(f)$.
• Values with magnitude less than  $0.0005$  are output in the program as "zero".

(1)   Compare the  red Gaussian pulse  $(A_1 = 1, \Delta t_1 = 1)$  with the  blue rectangular pulse  $(A_2 = 1, \Delta t_2 = 1)$ ⇒ default setting.
          What are the differences in the time and frequency domain?

• The Gaussian pulse theoretically reaches infinity in the time as well as in the frequency domain.
  
• Practically  $x_1(t)$  for  $|t| > 1.5$  and  $X_1(f)$  for  $|f| > 1.5$  are almost zero.
  
• The rectangle is strictly limited in time:  $x_2(|t| > 0.5) \equiv 0$.  $X_2(f)$  has shares in a much larger range than  $X_1(f)$.
  
• It holds  $X_1(f = 0) = X_2(f = 0)$  since the integral over the Gaussian pulse  $x_1(t)$  is equal to the integral over the rectangular pulse  $x_2(t)$.

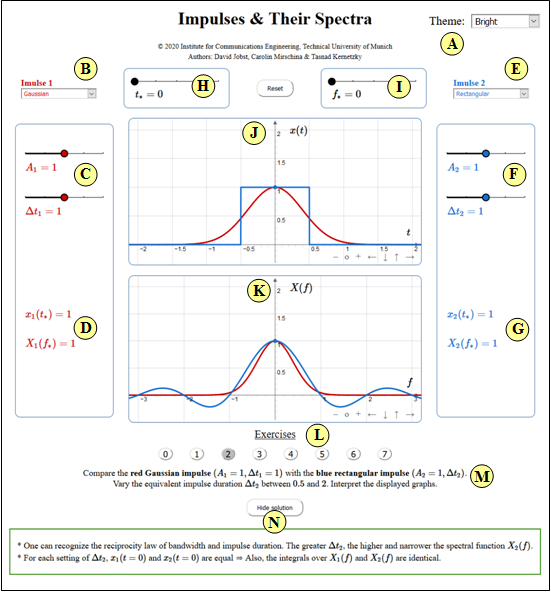
(2)   Compare the  red Gaussian pulse  $(A_1 = 1,  \Delta t_1 = 1)$ with the  blue rectangular pulse  $(A_2 = 1,  \Delta t_2)$.
          Vary the equivalent pulse duration  $\Delta t_2$  between  $0.5$  and  $2$.  Interpret the displayed graphs.

• One can recognize the reciprocity law of bandwidth and pulse duration.  The greater  $\Delta t_2$, the higher and narrower the spectral function  $X_2(f)$.
  
• For each setting of  $\Delta t_2$,  $x_1(t=0)$  and  $x_2(t=0)$  are equal   ⇒   Also, the integrals over  $X_1(f)$  and  $X_2(f)$  are identical.

(3)   Compare the  red Gaussian pulse  $(A_1 = 1,  \Delta t_1 = 1)$ with the  blue rectangular pulse  $(A_2 = 1,  \Delta t_2 = 0.5)$.
          Vary  $\Delta t_2$  between  $0.05$  and  $2$.  Interpret the displayed graphs and extrapolate the result.

• The blue spectrum is now twice as wide as the red one, but only half as high.  First zero of  $X_1(f)$  at  $f = 1$, of  $X_2(f)$  at  $f = 2$.
  
• Reduction of  $\Delta t_2$:  $X_2(f)$  lower and wider.  Very flat course at  $\Delta t_2 = 0.05$:  $X_2(f = 0)= 0.05$,  $X_2(f = \pm 3)= 0.048$.
  
• If one choose  $\Delta t_2 = \varepsilon \to 0$  (not possible in the program),  the result would be the almost constant, very small spectrum  $X_2(f)=A \cdot \varepsilon \to 0$.
  
• Increasing the amplitude to  $A=1/\varepsilon$  results in the constant spectral function  $X_2(f) = 1$  of the Dirac function  $\delta(t)$.  That means:
  
• $\delta(t)$  is approximated by a rectangle  $($width  $\Delta t = \varepsilon \to 0$,  height  $A = 1/\varepsilon \to \infty)$.  The weight of the Dirac function is one:  $x(t) = 1 \cdot \delta (t)$.

(4)   Compare the  rectangular pulse  $(A_1 = 1,   \Delta t_1 = 1)$  with the  triangular pulse  $(A_2 = 1,   \Delta t_2 = 1)$.  Interpret the spectral functions.

• The (normalized) spectrum of the rectangle  $x_1(t)$  with the (normalized) parameters  $A_1 = 1, \ \ \Delta t_1 = 1$  is:  $X_1(f)= {\rm si}(\pi\cdot f)= {\rm sinc}(f)$.
  
• The convolution of the rectangle  $x_1(t)$  with itself gives the triangle  $x_2(t) = x_1(t) \star x_1(t)$.  By the convolution theorem:   $X_2(f) = X_1(f)^2$.
  
• By squaring the  ${\rm sinc}(f)$–shaped spectral function  $X_1(f)$  the zeros of  $X_2(f)$  remain unchanged.  But now it holds that: $X_2(f) \ge 0$.

(5)   Compare the  trapezoidal pulse  $(A_1 = 1, \Delta t_1 = 1, r_1 = 0.5)$  with the  triangular pulse $(A_2 = 1,   \Delta t_2 = 1)$.
         Vary  $r_1$  between  $0$  and  $1$.  Interpret the spectral function  $X_1(f)$.

• The trapezoidal pulse with roll–off factor  $r_1= 0$  is identical to the rectangular pulse.  The "normalized spectrum" is  $X_1(f)= {\rm sinc}(f)$.
  
• The trapezoidal pulse with roll–off factor  $r_1= 1$  is identical to the triangular pulse.  The "normalized spectrum" is  $X_1(f)= {\rm sinc}^2(f)$.
  
• In both cases  $X_1(f)$  has equidistant zeros at  $\pm 1$,  $\pm 2$, ...  (none else);   $0 < r_1 < 1$:  depending on  $r_1$  further zeros.

(6)   Compare this  trapezoidal pulse  with the cosine roll-off pulse  $(A_2 = 1,\ \Delta t_2 = 1.0,\ r_2 = 0.5)$.
         Vary  $r_2$  between  $0$  and  $1$.  Interpret the spectral function  $X_2(f)$  for  $r_2 = 0.7$.

• With the same  $r= 0.5$  the cosine roll-off pulse  $X_2(f)$ is for  $f > 1$  greater in magnitude than the trapezoidal pulse.
  
• With the same roll-off factor  $(r_1 = r_2= 0.5)$  the drop of  $X_2(f)$  around the frequency  $f = 0.5$  is steeper than the drop of  $X_1(f)$.
  
• With  $r_1 = 0.5$  and  $r_2 = 0.7$  $x_1(t) \approx x_2(t)$  is valid and therefore also  $X_1(f) \approx X_2(f)$.  Comparable edge steepness.

(7)   Compare the  red trapezoidal pulse  $(A_1 = 1, \Delta t_1 = 1, \ r_1 = 1)$  with the  blue cosine roll-off pulse  $(A_2 = 1,\ \Delta t_2 = 1.0, \ r_2 = 1)$.
          Interpret the time function  $x_2(t)$  and the spectral function  $X_2(f)$  system theoretically.

• $x_2(t) = \cos^2(|t|\cdot \pi/2) \ \ \ \text{for} \ |t| \le 1$  is the  cosine square pulse.  Zeros at  $f = \pm 1$,  $\pm 2$, ...
  
• For the frequency  $f=\pm 0.5$  one obtains the spectral values  $X_2(f)=0.5$.  The asymptotic decline is shown here with  $1/f^3$.

Applet Manual

Screenshot

    (A)     Theme (changeable graphical user interface design)

• Dark:   dark background  (recommended by the authors)
• Bright:   white background  (recommended for beamers and printouts)
• Deuteranopia:   for users with pronounced green visual impairment
• Protanopia:   for users with pronounced red visual impairment

    (B)     Preselection for pulse shape  $x_1(t)$  (red curve)

    (C)     Parameter definition for  $x_1(t)$ 

    (D)     Numeric output for  $x_1(t_*)$  and  $X_1(f_*)$

    (E)     Preselection for pulse shape  $x_2(t)$  (blue curve)

    (F)     Parameter definition for  $x_2(t)$ 

    (G)     Numeric output for  $x_2(t_*)$  and  $X_2(f_*)$

    (H)     Setting the time  $t_*$  for the numeric output

    (I)     Setting the frequency  $f_*$  for the numeric output

    (J)     Graphic field for the time domain

    (K)     Graphic field for the frequency domain

    (L)     Selection of the exercise according to the numbers

    (M)     Task description and questions

    (N)     Show and hide sample solution

About the Authors

This interactive calculation tool was designed and implemented at the  Institute for Communications Engineering  at the  Technical University of Munich.

• The first version was created in 2005 by  Ji Li  as part of her diploma thesis with “FlashMX – Actionscript”  (Supervisor:  Günter Söder).
• In 2017 the program was redesigned by  David Jobst  (Ingenieurspraxis_Math, Supervisor: Tasnád Kernetzky ) via "HTML5".
• Last revision and English version 2020 by  Carolin Mirschina  in the context of a working student activity. 

Once again: Open Applet in new Tab

Open Applet in new Tab   Deutsche Version Öffnen