Difference between revisions of "Modulation Methods/Pulse Code Modulation"
| Line 16: | Line 16: | ||
*dieses Signal über den Kanal zu übertragen, wobei das empfängerseitige Signal $υ_{\rm C}(t)$ wegen des Entscheiders ebenfalls binär ist, | *dieses Signal über den Kanal zu übertragen, wobei das empfängerseitige Signal $υ_{\rm C}(t)$ wegen des Entscheiders ebenfalls binär ist, | ||
*schließlich aus dem Binärsignal $υ_{\rm C}(t)$ das analoge, wert– und zeitkontinuierliche Sinkensignal $υ(t)$ zu rekonstruieren ⇒ D/A–Wandlung. | *schließlich aus dem Binärsignal $υ_{\rm C}(t)$ das analoge, wert– und zeitkontinuierliche Sinkensignal $υ(t)$ zu rekonstruieren ⇒ D/A–Wandlung. | ||
| + | |||
| + | ==Prinzip und Blockschaltbild (2)== | ||
| + | [[File:P_ID1589__Mod_T_4_1_S1_neu.png | Blockschaltbild der Pulscodemodulation]] | ||
| + | |||
| + | |||
| + | Weiterhin ist zum obigen PCM–Blockschaltbild anzumerken: | ||
| + | |||
| + | |||
| + | *Der PCM–Sender (bzw. der A/D–Wandler) setzt sich aus den drei Funktionsblöcken Abtastung – Quantisierung – PCM–Codierung zusammen, die in den nächsten Abschnitten noch im Detail beschrieben werden. | ||
| + | |||
| + | |||
| + | *Der grau hinterlegte Block zeigt das digitale Übertragungssystem mit digitalem Sender und Empfänger (letzterer beinhaltet auch einen Entscheider), sowie dem analogen Übertragungskanal, gekennzeichnet durch den Frequenzgang $H_{\rm K}(f)$ und die Rauschleistungsdichte ${\it Φ}_n(f)$. | ||
| + | |||
| + | |||
| + | *Dieser Block wird in den ersten drei Kapiteln des Buches „Digitalsignalübertragung” eingehend behandelt. Im Kapitel 5 des gleichen Buches finden Sie auch digitale Kanalmodelle, die das Übertragungsverhalten anhand der Binärsignale $q_{\rm C}(t)$ und $υ_{\rm C}(t)$ phänomenologisch beschreiben. | ||
| + | |||
| + | |||
| + | *Weiter erkennt man aus dem Blockschaltbild, dass es für die Quantisierung empfängerseitig keine Entsprechung gibt. Deshalb wird sich auch bei fehlerfreier Übertragung, also für $υ_{\rm C}(t) = q_{\rm C}(t)$, das analoge Sinkensignal $υ(t)$ vom Quellensignal $q(t)$ unterscheiden. | ||
| + | |||
| + | |||
| + | *Als Maß für die Qualität des (digitalen) Übertragungssystems verwenden wir das Sinken–SNR als der Quotient der Leistungen von Nutzsignal $q(t)$ und Fehlersignal $ε(t) = υ(t) – q(t)$: | ||
| + | $$\rho_{v} = \frac{P_q}{P_\varepsilon}\hspace{0.3cm} {\rm mit}\hspace{0.3cm}P_q = \overline{q(t)^2}, | ||
| + | \hspace{0.2cm}P_\varepsilon = \overline{[v(t) - q(t)]^2}\hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | *Hierbei ist ideale Amplitudenanpassung vorausgesetzt, so dass im Idealfall (das heißt: Abtastung gemäß dem Abtasttheorem, bestmögliche Signalrekonstruktion, unendlich feine Quantisierung) das Sinkensignal $υ(t)$ mit dem Quellensignal $q(t)$ exakt übereinstimmen würde. | ||
| + | |||
| + | |||
| + | Wir möchten Sie bereits hier auf das 3–teilige Lernvideo Pulscodemodulation (Gesamtdauer 46:45) hinweisen, dass alle Aspekte der PCM beinhaltet. Das Prinzip wird im ersten Teil ausführlich erläutert. | ||
| + | |||
Revision as of 18:59, 19 June 2016
Prinzip und Blockschaltbild (1)
Nahezu alle heute eingesetzten Modulationsverfahren arbeiten digital. Deren Vorteile wurden schon im Kapitel 1.1 aufgeführt. Das erste Konzept zur digitalen Signalübertragung wurde bereits 1938 von Alec Reeves entwickelt und wird seit den 1960er Jahren unter dem Namen Pulscodemodulation (PCM) auch in der Praxis eingesetzt. Auch wenn sich viele der in den letzten Jahren konzipierten digitalen Modulationsverfahren von der PCM im Detail unterscheiden, so eignet sich diese doch sehr gut, um das Prinzip all dieser Verfahren zu erklären.
Die Aufgabe des PCM–Systems ist es,
- das analoge Quellensignal $q(t)$ in das Binärsignal $q_{\rm C}(t)$ umzusetzen – diesen Vorgang bezeichnet man auch als A/D–Wandlung,
- dieses Signal über den Kanal zu übertragen, wobei das empfängerseitige Signal $υ_{\rm C}(t)$ wegen des Entscheiders ebenfalls binär ist,
- schließlich aus dem Binärsignal $υ_{\rm C}(t)$ das analoge, wert– und zeitkontinuierliche Sinkensignal $υ(t)$ zu rekonstruieren ⇒ D/A–Wandlung.
Prinzip und Blockschaltbild (2)
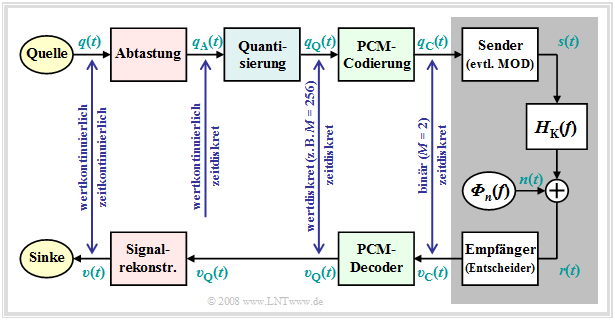
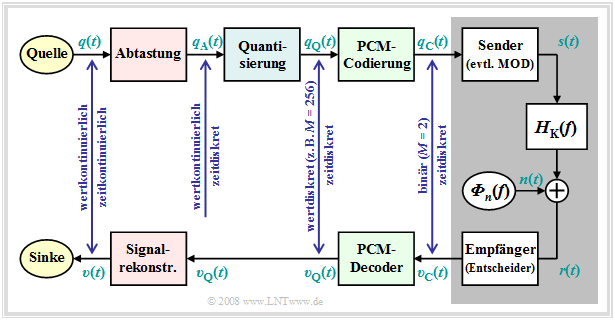
Weiterhin ist zum obigen PCM–Blockschaltbild anzumerken:
- Der PCM–Sender (bzw. der A/D–Wandler) setzt sich aus den drei Funktionsblöcken Abtastung – Quantisierung – PCM–Codierung zusammen, die in den nächsten Abschnitten noch im Detail beschrieben werden.
- Der grau hinterlegte Block zeigt das digitale Übertragungssystem mit digitalem Sender und Empfänger (letzterer beinhaltet auch einen Entscheider), sowie dem analogen Übertragungskanal, gekennzeichnet durch den Frequenzgang $H_{\rm K}(f)$ und die Rauschleistungsdichte ${\it Φ}_n(f)$.
- Dieser Block wird in den ersten drei Kapiteln des Buches „Digitalsignalübertragung” eingehend behandelt. Im Kapitel 5 des gleichen Buches finden Sie auch digitale Kanalmodelle, die das Übertragungsverhalten anhand der Binärsignale $q_{\rm C}(t)$ und $υ_{\rm C}(t)$ phänomenologisch beschreiben.
- Weiter erkennt man aus dem Blockschaltbild, dass es für die Quantisierung empfängerseitig keine Entsprechung gibt. Deshalb wird sich auch bei fehlerfreier Übertragung, also für $υ_{\rm C}(t) = q_{\rm C}(t)$, das analoge Sinkensignal $υ(t)$ vom Quellensignal $q(t)$ unterscheiden.
- Als Maß für die Qualität des (digitalen) Übertragungssystems verwenden wir das Sinken–SNR als der Quotient der Leistungen von Nutzsignal $q(t)$ und Fehlersignal $ε(t) = υ(t) – q(t)$:
$$\rho_{v} = \frac{P_q}{P_\varepsilon}\hspace{0.3cm} {\rm mit}\hspace{0.3cm}P_q = \overline{q(t)^2}, \hspace{0.2cm}P_\varepsilon = \overline{[v(t) - q(t)]^2}\hspace{0.05cm}.$$
- Hierbei ist ideale Amplitudenanpassung vorausgesetzt, so dass im Idealfall (das heißt: Abtastung gemäß dem Abtasttheorem, bestmögliche Signalrekonstruktion, unendlich feine Quantisierung) das Sinkensignal $υ(t)$ mit dem Quellensignal $q(t)$ exakt übereinstimmen würde.
Wir möchten Sie bereits hier auf das 3–teilige Lernvideo Pulscodemodulation (Gesamtdauer 46:45) hinweisen, dass alle Aspekte der PCM beinhaltet. Das Prinzip wird im ersten Teil ausführlich erläutert.