Aufgaben:Exercise 1.2: Coaxial Cable

• Return to book

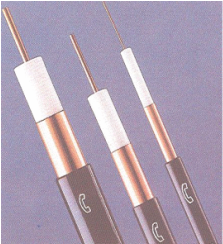
Der Frequenzgang eines Normalkoaxialkabels (Durchmesser des Innenleiters: 2.6 mm, Außendurchmesser: 9.5 mm) der Länge $l$ lautet für Frequenzen $f$ > 0: $$H(f) = {\rm e}^{-\alpha_{0\hspace{0.02cm}} \hspace{0.05cm} \cdot \hspace{0.05cm} l} \cdot {\rm e}^{-(\alpha_1 + {\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm} \beta_1)\hspace{0.05cm} \cdot \hspace{0.05cm} f \cdot \hspace{0.05cm} l}\cdot {\rm e}^{-(\alpha_2 + {\rm j}\hspace{0.05cm} \cdot \beta_2) \hspace{0.05cm} \cdot \hspace{0.05cm} \sqrt{f} \cdot \hspace{0.05cm} l}.$$

Der erste, von den Ohmschen Verlusten herrührende Term in dieser Gleichung wird durch die sog. kilometrische Dämpfung $α_0 =$ 0.00162 Np/km beschrieben.

Der frequenzproportionale Dämpfungsanteil ⇒ $α_1 · f · l$ mit $α_1 =$ 0.000435 Np/(km · MHz) geht auf die Querverluste zurück. Er macht sich erst bei sehr hohen Frequenzen bemerkbar und wird im Folgenden vernachlässigt. Auch die frequenzproportionale Phase $β_1 · f · l$ mit $β_1 =$ 21.78 rad/(km · MHz) wird außer Acht gelassen werden, da diese nur eine für alle Frequenzen gleiche Laufzeit zur Folge hat.

Der Koaxialkabel–Frequenzgang wird deshalb für Frequenzen zwischen 200 kHz und 400 MHz im Wesentlichen durch den Einfluss der Dämpfungskonstanten $α_2 =$ 0.2722 Np/(km · MHz $^{0.5}$) und der Phasenkonstanten $β_2 =$ 0.2722 rad/(km · MHz $^{0.5}$) bestimmt, die auf den so genannten Skineffekt zurückzuführen sind: $$H(f) = K \cdot {\rm e}^{-(\alpha_2 + {\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm} \beta_2)\hspace{0.05cm} \cdot \hspace{0.05cm} \sqrt{f} \hspace{0.05cm} \cdot \hspace{0.05cm} l}\hspace{0.3 cm} (f > 0).$$ Aufgrund der gleichen Zahlenwerte von $α_2$ und $β_2$ kann hierfür auch geschrieben werden: $$H(f) = K \cdot {\rm e}^{- \sqrt{2{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm} f/f_0} },$$ wobei der Parameter $f_0$ die Konstanten $α_2$ und $β_2$ sowie die Kabellänge $l$ berücksichtigt.

Hinweis: Diese Aufgabe bezieht sich auf den Theorieteil von Kapitel 1.1.

Fragebogen

1

Multiple-Choice Frage

	Falsch
	Richtig

2

Input-Box Frage

$\alpha$ =

Musterlösung

Solution

a)

b)

c)

d)

e)

f)

g)