Difference between revisions of "Aufgaben:Exercise 1.3: Measured Step Response"
(Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Lineare zeitinvariante Systeme/Systembeschreibung im Zeitbereich}} Datei:P_ID817__LZI_A_1_3.png |right|Gemessene Sprungantwort (Auf…“) |
|||
| Line 3: | Line 3: | ||
[[File:P_ID817__LZI_A_1_3.png |right|Gemessene Sprungantwort (Aufgabe A1.3)]] | [[File:P_ID817__LZI_A_1_3.png |right|Gemessene Sprungantwort (Aufgabe A1.3)]] | ||
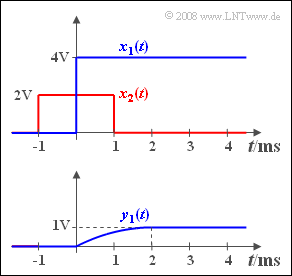
| + | An den Eingang eines linearen zeitinvarianten (LZI–)Übertragungssystems mit Frequenzgang $H(f)$ und Impulsantwort $h(t)$ wird ein sprungförmiges Signal angelegt (blaue Kurve): | ||
| + | $$x_1(t) = 4\,{\rm V} \cdot \gamma(t).$$ | ||
| + | Das gemessene Ausgangssignal $y_1(t)$ hat dann den in der unteren Grafik dargestellten Verlauf. Mit $T =$ 2 ms kann dieses Signal im Bereich von 0 bis $T$ wie folgt beschrieben werden: | ||
| + | $$y_1(t) = 2\,{\rm V} \cdot\left[ {t}/{T} - 0.5 \cdot ({t}/{T})^2\right].$$ | ||
| + | |||
| + | Ab $t = T =$ 2 ms ist $y_1(t)$ konstant gleich 1 V. | ||
| + | |||
| + | In der letzten Teilaufgabe (e) wird nach dem Ausgangssignal $y_2(t)$ gefragt, wenn am Eingang ein symmetrischer Rechteckimpuls $x_2(t)$ der Dauer $T =$ 2 ms anliegt (siehe roter Kurvenzug in der oberen Grafik). | ||
| + | |||
| + | '''Hinweis:''' Diese Aufgabe bezieht sich auf den Theorieteil von [[Lineare_zeitinvariante_Systeme/Systembeschreibung_im_Zeitbereich|Kapitel 1.2]]. | ||
| + | Für den Rechteckimpuls $x_2(t)$ kann mit $A =$ 2 V auch geschrieben werden: | ||
| + | $$x_2(t) = A \cdot \left[\gamma(t + {T}/{2}) - \gamma(t - {T}/{2})\right].$$ | ||
| + | Der Frequenzgang $H(f)$ des hier betrachteten LZI–Systems kann dem Angabenblatt zu Aufgabe A3.8 im Buch „Signaldarstellung” entnommen werden. Allerdings sind die Abszissen– und Ordinatenparameter entsprechend anzupassen. Zur Lösung dieser [[Aufgaben:3.8_Dreimal_Faltung|Aufgabe A1.3]] wird $H(f)$ jedoch nicht explizit benötigt. | ||
Revision as of 10:41, 10 July 2016
An den Eingang eines linearen zeitinvarianten (LZI–)Übertragungssystems mit Frequenzgang $H(f)$ und Impulsantwort $h(t)$ wird ein sprungförmiges Signal angelegt (blaue Kurve): $$x_1(t) = 4\,{\rm V} \cdot \gamma(t).$$ Das gemessene Ausgangssignal $y_1(t)$ hat dann den in der unteren Grafik dargestellten Verlauf. Mit $T =$ 2 ms kann dieses Signal im Bereich von 0 bis $T$ wie folgt beschrieben werden: $$y_1(t) = 2\,{\rm V} \cdot\left[ {t}/{T} - 0.5 \cdot ({t}/{T})^2\right].$$
Ab $t = T =$ 2 ms ist $y_1(t)$ konstant gleich 1 V.
In der letzten Teilaufgabe (e) wird nach dem Ausgangssignal $y_2(t)$ gefragt, wenn am Eingang ein symmetrischer Rechteckimpuls $x_2(t)$ der Dauer $T =$ 2 ms anliegt (siehe roter Kurvenzug in der oberen Grafik).
Hinweis: Diese Aufgabe bezieht sich auf den Theorieteil von Kapitel 1.2. Für den Rechteckimpuls $x_2(t)$ kann mit $A =$ 2 V auch geschrieben werden: $$x_2(t) = A \cdot \left[\gamma(t + {T}/{2}) - \gamma(t - {T}/{2})\right].$$ Der Frequenzgang $H(f)$ des hier betrachteten LZI–Systems kann dem Angabenblatt zu Aufgabe A3.8 im Buch „Signaldarstellung” entnommen werden. Allerdings sind die Abszissen– und Ordinatenparameter entsprechend anzupassen. Zur Lösung dieser Aufgabe A1.3 wird $H(f)$ jedoch nicht explizit benötigt.
Fragebogen
Musterlösung
- a)
- b)
- c)
- d)
- e)
- f)
- g)