Difference between revisions of "Aufgaben:Exercise 1.3Z: Exponentially Decreasing Impulse Response"
From LNTwww
(Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Lineare zeitinvariante Systeme/Systembeschreibung im Zeitbereich}} Datei:P_ID819__LZI_Z_1_3.png |right|Exponentiell abfallende Impu…“) |
|||
| Line 5: | Line 5: | ||
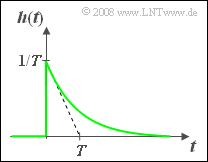
Gemessen wurde die Impulsantwort $h(t)$ eines LZI–Systems, die für alle Zeiten $t$ < 0 identisch 0 ist und für $t$ > 0 entsprechend einer Exponentialfunktion abfällt: | Gemessen wurde die Impulsantwort $h(t)$ eines LZI–Systems, die für alle Zeiten $t$ < 0 identisch 0 ist und für $t$ > 0 entsprechend einer Exponentialfunktion abfällt: | ||
$$h(t) = \frac{1}{T} \cdot {\rm e}^{-t/T}.$$ | $$h(t) = \frac{1}{T} \cdot {\rm e}^{-t/T}.$$ | ||
| − | Der Funktionsparameter sei $T =$ 1 ms. In der Teilaufgabe | + | Der Funktionsparameter sei $T =$ 1 ms. In der Teilaufgabe 3) ist nach der 3dB–Grenzfrequenz $f_{\rm G}$ gefragt, die wie folgt implizit definiert ist: |
$$|H(f = f_{\rm G})| = \frac{1}{\sqrt{2}} \cdot|H(f = 0)| .$$ | $$|H(f = f_{\rm G})| = \frac{1}{\sqrt{2}} \cdot|H(f = 0)| .$$ | ||
'''Hinweis:''' Diese Aufgabe bezieht sich auf die theoretischen Grundlagen von [[Lineare_zeitinvariante_Systeme/Systembeschreibung_im_Zeitbereich|Kapitel 1.2]]. Gegeben ist das folgende bestimmte Integral: | '''Hinweis:''' Diese Aufgabe bezieht sich auf die theoretischen Grundlagen von [[Lineare_zeitinvariante_Systeme/Systembeschreibung_im_Zeitbereich|Kapitel 1.2]]. Gegeben ist das folgende bestimmte Integral: | ||
| Line 12: | Line 12: | ||
===Fragebogen=== | ===Fragebogen=== | ||
| + | |||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Berechnen Sie den Frequenzgang $H(f)$. Welcher Wert ergibt sich für $f =$ 0? |
| − | |type=" | + | |type="{}"} |
| − | + | $H(f = 0) =$ { 1 } | |
| − | + | ||
| + | |||
| + | {Welchen Wert besitzt die Impulsantwort zur Zeit $t =$ 0? | ||
| + | |type="{}"} | ||
| + | $h(t = 0) =$ { 500 } 1/s | ||
| − | { | + | {Berechnen Sie die 3dB–Grenzfrequenz $f_{\rm G}$. |
|type="{}"} | |type="{}"} | ||
| − | $\ | + | $f_{\rm G} =$ { 159 } Hz |
| + | |||
| + | |||
| + | {Welche der nachfolgenden Aussagen sind zutreffend? | ||
| + | |type="[]"} | ||
| + | + Das betrachtete System ist kausal. | ||
| + | - Das betrachtete System hat Hochpass–Charakter. | ||
| + | - Liegt am Systemeingang ein Cosinussignal der Frequenz $f_{\rm G}$ an, so ist das Ausgangssignal ebenfalls cosinusförmig. | ||
Revision as of 18:55, 12 July 2016
Gemessen wurde die Impulsantwort $h(t)$ eines LZI–Systems, die für alle Zeiten $t$ < 0 identisch 0 ist und für $t$ > 0 entsprechend einer Exponentialfunktion abfällt: $$h(t) = \frac{1}{T} \cdot {\rm e}^{-t/T}.$$ Der Funktionsparameter sei $T =$ 1 ms. In der Teilaufgabe 3) ist nach der 3dB–Grenzfrequenz $f_{\rm G}$ gefragt, die wie folgt implizit definiert ist: $$|H(f = f_{\rm G})| = \frac{1}{\sqrt{2}} \cdot|H(f = 0)| .$$ Hinweis: Diese Aufgabe bezieht sich auf die theoretischen Grundlagen von Kapitel 1.2. Gegeben ist das folgende bestimmte Integral: $$\int_{ 0 }^{ \infty } \frac{1}{1+x^2} \hspace{0.1cm}{\rm d}x = \frac{\pi}{2} .$$
Fragebogen
Musterlösung
1.
2.
3.
4.
5.
6.
7.