Aufgaben:Exercise 1.4Z: Sum of Ternary Quantities

• Return to book

Gegeben seien die ternären Zufallsgrößen

• $x ∈ {–2, 0, +2}$,

• $y ∈ {–1, 0, +1}$.

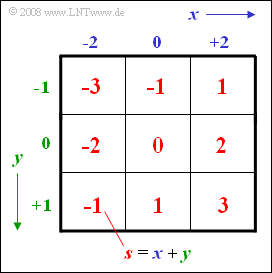
Diese beiden Ternärwerte treten jeweils mit gleicher Wahrscheinlichkeit auf. Daraus wird als eine neue Zufallsgröße die Summe $s = x + y$ gebildet.

Nebenstehendes Schema zeigt, dass die Summe s alle ganzzahligen Werte zwischen –3 und +3 annehmen kann\[ s \in \{-3, -2, -1, 0, +1, +2, +3\}\],

Hinweis: Diese Aufgabe bezieht sich auf den Lehrstoff von Kapitel 1.3. Eine Zusammenfassung der theoretischen Grundlagen mit Beispielen bringt das nachfolgende Lernvideo:

Fragebogen

1

Berechnen Sie die Wahrscheinlichkeit, dass die Summe $s$ positv ist:

$Pr(s>0)$ =

2

Berechnen Sie die Wahrscheinlichkeit, dass sowohl die Eingangsgröße x als auch die Summe s positiv sind:

$Pr((x>0) \cap (s>0))$ =

3

Berechnen Sie die bedingte Wahrscheinlichkeit, dass die Eingangsgröße x > 0 ist, wenn s > 0 gilt:

$Pr(x>0|s>0)$ =

4

Berechnen Sie die bedingte Wahrscheinlichkeit, dass die Summe s positiv ist, wenn die Eingangsgröße x > 0 ist:

$Pr(s>0|x>0)$ =

Musterlösung

Solution

a)

b)

c)

d)

e)

f)

g)