Aufgaben:Exercise 2.6Z: Synchronous Demodulator

• Return to book

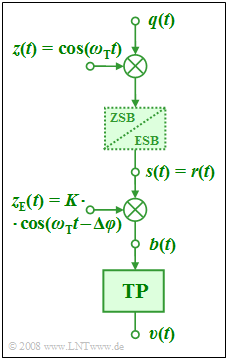
Das dargestellte Blockschaltbild zeigt ein Übertragungssystem mit Amplitudenmodulation (AM) und Synchrondemodulator (SD). Das Quellensignal bestehe aus zwei harmonischen Schwingungen mit den Frequenzen f₂ = 2 kHz und f₅ = 5 kHz:

$$q(t) = {2 \, \rm V} \cdot {\rm cos}(\omega_2 t )+ {1 \, \rm V} \cdot {\rm sin}(\omega_5 t ) .$$

Dieses Signal wird bei AM mit dem dimensionslosen Trägersignal z(t) = cos(ω_T · t) der Trägerfrequenz f_T = 50 kHz multipliziert. Bei Zweiseitenbandmodulation (ZSB–AM) ist der gestrichelt eingezeichnete Block unerheblich, so dass für das Sendesignal gilt:

$$s(t) = q(t) \cdot {\rm cos}(\omega_{\rm T} t ) .$$

Im Synchrondemodulator wird das Empfängersignal r(t), das bei idealem Kanal identisch mit s(t) ist, mit dem empfangsseitigem Trägersignal z_E(t) multipliziert, wobei gilt:

$$z_{\rm E}(t) = K \cdot {\rm cos}(\omega_{\rm T} t - \Delta \varphi ) .$$

Dieses Signal sollte nicht nur frequenzsynchron mit z(t) sein, sondern auch phasensynchron – daher der Name „Synchrondemodulator”. Der obige Ansatz berücksichtigt einen Phasenversatz Δφ zwischen z(t) und z_E(t), der idealerweise 0 sein sollte, sich bei realen Systemen aber oft nicht vermeiden lässt.

Das Ausgangssignal b(t) des zweiten Multiplizierers beinhaltet neben dem gewünschten NF-Anteil auch Anteile um die doppelte Trägerfrequenz. Durch einen idealen Tiefpass – z.B. mit der Grenzfrequenz f_T – lässt sich das Sinkensignal υ(t) gewinnen, das im Idealfall gleich dem Quellensignal q(t) sein sollte.

Die Multiplikation beim Sender mit dem Trägersignal z(t) führt im Allgemeinen zu zwei Seitenbändern. Bei der Einseitenbandmodulation (ESB–AM) wird nur eines der beiden Bänder übertragen, zum Beispiel das untere Seitenband (USB). Damit erhält man bei idealem Kanal:

$$r(t) = s(t)= {1 \, \rm V} \cdot {\rm cos}((\omega_{\rm T} - \omega_2 )t ) - {0.5 \, \rm V} \cdot {\rm sin}((\omega_{\rm T} - \omega_5 )t ) .$$

Hier führt die Synchrondemodulation unter Berücksichtigung eines Phasenversatzes Δφ, der Konstante <nobr>K = 4</nobr> sowie des nachgeschalteten Tiefpasses zu folgendem verfälschten Sinkensignal:

$$v(t)= {1 \, \rm V} \cdot \frac{1}{2}\cdot 4 \cdot{\rm cos}( \omega_2 t - \Delta \varphi)+ {0.5 \, \rm V} \cdot \frac{1}{2}\cdot 4 \cdot{\rm sin}( \omega_5 t - \Delta \varphi)$$

$$\Rightarrow \hspace{0.5cm}v(t)= {2 \, \rm V} \cdot{\rm cos}( \omega_2 t - \Delta \varphi)+ {1 \, \rm V} \cdot{\rm sin}( \omega_5 t - \Delta \varphi)$$

Im Idealfall phasensynchroner Demodulation (Δφ = 0) gilt wieder

$$v(t) = q(t).$$

Hinweis: Diese Aufgabe bezieht sich auf den Theorieteil von Kapitel 2.3 in diesem Buch. Die Thematik „Amplitudenmodulation/Synchrondemodulator” wird im Buch „Modulationsverfahren” noch ausführlich diskutiert werden.

Gegeben sind die folgenden trigonometrischen Zusammenhänge:

$$\cos^2(\alpha) = \frac{1}{2} \cdot \left [ 1 + \cos(2\alpha) \right ] \hspace{0.05cm}, \\ \cos(\alpha) \cdot \cos(\beta) = \frac{1}{2} \cdot \left[ \cos(\alpha - \beta)+ \cos(\alpha + \beta) \right] \\ \sin(\alpha) \cdot \cos(\beta) = \frac{1}{2} \cdot \left[ \sin(\alpha - \beta)+ \sin(\alpha + \beta) \right] \hspace{0.05cm}.$$

Fragebogen

1

Wie lautet das Sinkensignal υ(t) bei phasensynchroner Synchrondemodulation (Δφ = 0) und ZSB-AM? Wie ist K zu wählen, damit υ(t) = q(t) gilt?

$K$ =

2

Es gelte K = 2. Berechnen Sie das Sinkensignal υ(t) unter Berücksichtigung eines Phasenversatzes Δφ. Welche der folgenden Aussagen treffen zu?

	Unabhängig von Δφ gilt υ(t) = q(t).
	Δφ ≠ 0 führt zu einer frequenzunabhängigen Dämpfung.
	Ein Phasenversatz Δφ ≠ 0 führt zu Dämpfungsverzerrungen.
	Ein Phasenversatz Δφ ≠ 0 führt zu Phasenverzerrungen.
	Mit Δφ = – 60° gilt υ(t) = q(t)/2.

3

Welche Aussagen gelten bei Synchrondemodulation des ESB–Signals (siehe Angabenseite), wenn ein Phasenversatz um Δφ berücksichtigt wird?

	Unabhängig von Δφ gilt υ(t) = q(t).
	Δφ ≠ 0 führt zu einer frequenzunabhängigen Dämpfung.
	Ein Phasenversatz Δφ ≠ 0 führt zu Dämpfungsverzerrungen.
	Ein Phasenversatz Δφ ≠ 0 führt zu Phasenverzerrungen.
	Mit Δφ = – 60° gilt υ(t) = q(t)/2.

Musterlösung

Solution

1.  Für das Bandpass–Signal nach dem zweiten Multiplizierer gilt:

$$b(t) = r(t) \cdot z_{\rm E}(t)= q(t) \cdot z(t) \cdot z_{\rm E}(t)= K \cdot q(t)\cdot \cos^2(\omega_{\rm T} t).$$

Mit der trigonometrischen Beziehung

$$\cos^2(\omega_{\rm T} t) = \frac{1}{2} \cdot\left[ 1 + \cos(2\omega_{\rm T} t)\right]$$

erhält man

$$b(t) = \frac{K}{2} \cdot q(t) + \frac{K}{2} \cdot q(t)\cdot \cos(2\omega_{\rm T} t).$$

Der zweite Anteil liegt um die doppelte Trägerfrequenz und wird durch den Tiefpass – zum Beispiel mit der Grenzfrequenz f_T – entfernt. Damit erhält man:

$$v(t) = \frac{K}{2} \cdot q(t) .$$

Mit K = 2 ergibt sich eine ideale Demodulation:

$$v(t) = q(t) .$$

2.  Unter Berücksichtigung der Beziehung

$$\cos(\omega_{\rm T} t) \cdot \cos(\omega_{\rm T} t - \Delta \varphi) = \frac{1}{2} \cdot \left[ \cos(\Delta \varphi)+ \cos(2\omega_{\rm T} t - \Delta \varphi) \right]$$

sowie des nachgeschalteten Tiefpasses, der wieder den Anteil um die doppelte Trägerfrequenz entfernt, erhält man hier mit K = 2:

$$v(t) = q(t) \cdot \cos(\Delta \varphi).$$

Das heißt, ein Phasenversatz Δφ führt hier nur zu einer frequenzunabhängigen Dämpfung und nicht zu Dämpfungs– oder Phasenverzerrungen. Ein Phasenversatz um ±60° hat jeweils eine Halbierung des Signals zur Folge. Richtig sind demnach die Lösungsvorschläge 2 und 5.

3.  Richtig ist hier der Lösungsvorschlag 4. Bei beiden Summanden tritt genau der gleiche Phasenversatz Δφ auf, und es kommt hier zu Phasenverzerrungen:

$$v(t)= {2 \, \rm V} \cdot{\rm cos}( \omega_2 \cdot (t - \tau_2))+ {1 \, \rm V} \cdot{\rm sin}( \omega_5 t \cdot (t - \tau_5)),$$

$${\rm wobei}\hspace{0.5cm}\tau_2 = \frac{\Delta \varphi}{\omega_2} \hspace{0.5cm}\ne \hspace{0.5cm} \tau_5 = \frac{\Delta \varphi}{\omega_5}.$$

Ein Phasenversatz von 60° entsprechend π/3 führt hier zu den Verzögerungszeiten:

$$\tau_2 = \frac{\pi/3}{2 \pi \cdot 2\,\,{\rm kHz }} \approx 83.3\,{\rm \mu s }, \hspace{0.5cm} \tau_5 = \frac{\pi/3}{2 \pi \cdot 5\,\,{\rm kHz }} \approx 33.3\,{\rm \mu s }.$$

Das niederfrequentere Signal wird also stärker verzögert.