Aufgaben:Exercise 2.5Z: Square Wave

• Return to book

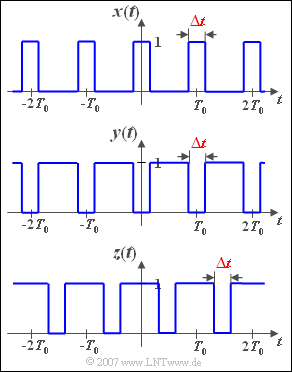
Das mit der Zeit $T_0$ periodische Signal $x(t)$ wird durch den einzigen Parameter $\Delta t$ beschrieben; die Amplitude der Rechteckimpulse sei jeweils $1$. Da $\x(t)$ gerade ist, sind alle Sinuskoeffizienten $B_n = 0$.

Der Gleichsignalkoeffizient ist $A_0 = \Delta t/T_0$ und für die Cosinuskoeffizienten gilt:

$$A_n=\frac{2}{n\pi}\cdot \sin(n\pi \Delta t/T_0).$$

In den Teilaufgaben 1) und 2) wird das Signal $x(t)$ für die zwei Parameterwerte $\Delta t/T_0 = 0.5$ bzw. $\Delta t/T_0 = 0.25$ analysiert. Danach betrachten wir die beiden ebenfalls in der Abbildung dargestellten Signale $y(t)$ und $z(t)$, jeweils mit $\Delta t/T_0 = 0.25$.

Hinweis: Die Aufgabe bezieht sich auf die theoretischen Grundlagen von Kapitel 2.4. Diese sind in zwei Lernvideos zusammengefasst:

Zur Berechnung der Fourierkoeffizienten

Eigenschaften und Genauigkeit der Fourierreihe

Fragebogen

1

Welche Aussagen gelten für das Signal $x(t)$ mit $\Delta t/T_0 = 0.5$?

	Die Spektralfunktion ${X(f)}$ beinhaltet eine Diracfunktion bei $f = 0$ mit dem Gewicht $0.5$.
	Die Spektralfunktion ${X(f)}$ beinhaltet Diraclinien bei allen Vielfachen der Grundfrequenz $f_0 = 1/T_0$.
	Die Spektralfunktion ${X(f)}$ beinhaltet Diraclinien bei ungeradzahligen Vielfachen der Grundfrequenz $f_0$.
	Die Spektrallinie bei $f_0$ hat das Gewicht $2/\pi$.
	Die Spektrallinie bei $–f_0$ hat das Gewicht $1/\pi$.

2

Welche Aussagen gelten für das Signal $x(t)$ mit $\Delta t/T_0 = 0.25$?

	Die Spektralfunktion ${X(f)}$ beinhaltet Diraclinien bei allen ungeraden Vielfachen der Grundfrequenz $f_0$.
	${X(f)}$ hat Diraclinien bei $\pm2f_0$, $\pm6f_0$, $\pm10f_0$, usw.
	${X(f)}$ hat Diraclinien bei $\pm4f_0$, $\pm8f_0$, $\pm12f_0$, usw.
	Die Spektrallinie bei $2f_0$ hat das Gewicht $1/(2\pi)$.

3

Wie groß ist der Gleichanteil des Signals ${y(t)}$?

Signal $y(t)$: $A_0=$

4

Welcher Zusammenhang besteht zwischen den Signalen $x(t)$ und ${y(t)}$? Geben Sie mit Hilfe dieser Überlegungen die Fourierkoeffizienten von ${y(t)}$ an. Wie groß sind die Koeffizienten $A_1$ und $A_2$ dieses Signals?

Signal $y(t)$: $A_1=-$

Signal $y(t)$: $A_2 = -$

5

Welcher Zusammenhang besteht zwischen den Signalen ${y(t)}$ und ${z(t)}$? Wie groß sind die Koeffizienten $A_1$ und $A_2$ des Signals ${z(t)}$? Überprüfen Sie das Ergebnis anhand der angebenen Koeffizienten des Signals $x(t)$.

Signal $z(t)$: $A_1 =$

Signal $z(t)$: $A_2 = -$

Musterlösung

Solution

1. Die Spektralfunktion beinhaltet eine Diracfunktion bei $f = 0$ mit dem Gewicht $0.5$ (Gleichanteil) sowie weitere Spektrallinien bei ungeradzahligen Vielfachen ($n = \pm1, \pm3, \pm5,...$) von f0. Die Gewichte bei $\pm f_0$ sind jeweils $A_1/2 = 1/\pi$. Richtig sind somit die Aussagen 1, 3 und 5.

2. Bei allen ungeradzahligen Vielfachen der Grundfrequenz existieren Spektrallinien, zusätzlich noch bei den $2–$, $6–$ und $10–$fachen. Beispielsweise gilt $A_2 = 1/\pi$. Die Spektrallinie bei $2f_0$ hat somit das Gewicht $A_2/2 = 1/(2\pi)$. Für $n = 4$, $n = 8$, usw. sind dagegen die Koeffizienten $A_n = 0$, da für die Sinusfunktion gilt: $sin(\pi) = sin(2\pi) = ... = 0$. Richtig sind somit die Aussagen 1, 2 und 4.

3. Aus der grafischen Darstellung des Signals ${y(t)}$ wird deutlich, dass $A_0 = 0.75$ gelten muss. Zum gleichen Ergebnis kommt man über die Beziehung:

$$A_0^{(y)}=1-A_0^{(x)}=1-0.25\hspace{0.15cm}\underline{=0.75}.$$

4. Es gilt ${y(t)} = 1 – x(t)$. Für $n \neq 0$ ergeben sich somit die gleichen Fourierkoeffizienten wie für das Signal $x(t)$, jedoch mit negativen Vorzeichen. Inbesondere gilt:

$$A_1=-\frac{2}{\pi}\sin\Bigg(\frac{\pi}{4}\Bigg)= -\frac{\sqrt2}{\pi}\hspace{0.15cm}\underline{\approx -0.450},$$

$$A_2=-\frac{1}{\pi}\hspace{0.15cm}\underline{ \approx - 0.318}.$$

5. Es gilt ${z(t)} = y(t – T_0/2)$. Mit der Fourierreihendarstellung von ${y(t)}$ folgt daraus:

$$z(t)=A_0+A_1^{(y)}\cos(\omega_0(t-\frac{T_0}{2}))+A_2^{(y)}\cos(2\omega_0(t-\frac{T_0}{2}))+\\+A_3^{(y)}\cos(3\omega_0(t-\frac{T_0}{2}))+\ldots$$

$$\Rightarrow \quad z(t)=A_0-A_1^{(y)}\cos(\omega_0 t)+A_2^{(y)}\cos(2\omega_0 t)-A_3^{(y)}\cos(3\omega_0 t)+\ldots$$

Damit erhält man:

$$A_1^{(z)}=-A_1^{(y)}=\frac{\sqrt2}{\pi}\hspace{0.15cm}\underline{=+0.450}, \hspace {0.5cm} A_2^{(z)}=A_2^{(y)}=-\frac{1}{\pi}\hspace{0.15cm}\underline{=-0.318}.$$

Das gleiche Ergebnis erhält man ausgehend von den gegebenen Koeffizienten mit $\Delta t/T_0 = 0.75$:

$$A_1^{(z)}={2}/{\pi} \cdot \sin({3}/{4}\cdot \pi)={\sqrt2}/{\pi}, \hspace {0.5cm}A_2^{(z)}= {1}/{\pi} \cdot \sin({3}/{2} \cdot \pi) =-{1}/{\pi}.$$