Loading [MathJax]/jax/output/HTML-CSS/fonts/TeX/fontdata.js

Difference between revisions of "Aufgaben:Exercise 1.6Z: Ternary Markov Source"

From LNTwww
Line 121: Line 121:
  
  
−
[[Category:Aufgaben zu Informationstheorie und Quellencodierung|^1.2 Nachrichtenquellen mit Gedächtnis^]]
+
[[Category:Aufgaben zu Informationstheorie|^1.2 Nachrichtenquellen mit Gedächtnis^]]

Revision as of 17:26, 24 November 2016

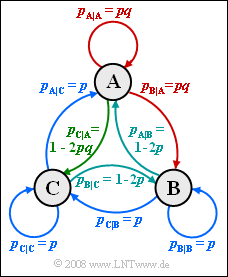
P ID2254 Inf Z 1 6.png
Die Grafik zeigt eine Markovquelle mit M = 3 Zuständen A, B und C. Für die beiden Parameter dieses Markovprozesses soll gelten:
0≤p≤0.5,0≤q≤1.
Aufgrund der Markoveigenschaft dieser Quelle kann die Entropie auf unterschiedliche Weise ermittelt werden:
  • Man berechnet die beiden ersten Entropienäherungen H1 und H2. Dann gilt:
H=2⋅H2−H1.
  • Nach der so genannten direkten Berechnungsmethode kann die Entropie aber auch wie folgt berechnet werden (insgesamt 9 Terme):
H=pAA⋅ld1pA|A+pAB⋅ld1pB|A+...,
pAA=pA⋅pA|A,pAB=pA⋅pB|A,...
Hinwis: Die Aufgabe gehört zum Themenkomplex von Kapitel 1.2.


Fragebogen

1

Für welche Parameter p, q ergibt sich die maximale Entropie pro Symbol?

p =

q =

Hmax =

bit/Symbol

2

Es sei p = 1/4 und q = 1. Welcher Wert ergibt sich in diesem Fall für die erste Entropienäherung?

p=1/4,q=1:  H1 =

bit/Symbol

3

Weiterhin gelte p = 1/4 und q = 1. Welcher Wert ergibt sich in diesem Fall für die zweite Entropienäherung?

p=1/4,q=1:  H2 =

bit/Symbol

4

Wie groß ist die Quellenentropie mit p = 1/4, q = 1?

p=1/4,q=1:  H =

bit/Symbol

5

Wie groß ist die Quellenentropie mit p = 1/2, q = 0?

p=1/2,q=0:  H =

bit/Symbol


Musterlösung

Solution

Hinweis: Aus Platzgründen verwenden wir in der Musterlösung „ld” anstelle von „log2”.
a)  Die maximale Entropie ergibt sich dann, wenn die Symbole A, B und C gleichwahrscheinlich und die Symbole innerhalb der Folge statistisch voneinander unabhängig sind. Dann muss gelten:
  • pA = pA|A = pA|B = pA|C = 1/3,
  • pB = pB|A = pB|B = pB|C = 1/3,
  • pC = pC|A = pC|B = pC|C = 1/3.
Beispielsweise erhält man aus pC|C = 1/3 der Wert p = 1/3. Berücksichtigt man noch pA|A = q · p, so folgt q = 1. Damit ergibt sich die maximale Entropie Hmax = ld 3 = 1.585 bit/Symbol.
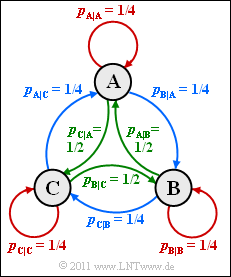
P ID2255 Inf Z 1 6b.png
2.  Mit den Parameterwerten p = 1/4 und q = 1 ergibt sich das nebenstehende Übergangsdiagramm, das folgende Symmetrien aufweist:
  • pA|A = pB|B = pC|C = 1/4 (rot markiert),
  • pA|B = pB|C = pC|A = 1/2 (grün markiert),
  • pA|C = pB|A = pC|B = 1/4 (blau markiert).
Es ist offensichtlich, dass die Symbolwahrscheinlichkeiten alle gleich sind:
pA=pB=pC=1/3
⇒H1=ld3=1.585bit/Symbol_.
3.  Für die zweite Entropienäherung benötigt man die 32 = 9 Verbundwahrscheinlichkeiten. Mit dem Ergebnis der Teilaufgabe b) erhält man hierfür:
pAA=pBB=pCC=pAC=pBA=pCB=1/12,pAB=pBC=pCA=1/6
⇒H2=12⋅[6⋅112⋅ld12+3⋅16⋅ld6]==14⋅ld4+14⋅ld3+14⋅ld2+14⋅ld3=34+ld32=1.5425bit/Symbol_.
4.  Aufgrund der Markoveigenschaft der Quelle gilt
H=2⋅H2−H1=[3/2+ld3]−ld3=1.5bit/Symbol_.
Zum gleichen Ergebnis würde man mit folgender Rechnung kommen:
H=pAA⋅ld1pA|A+pAB⋅ld1pB|A+...=6⋅112⋅ld4+3⋅116⋅ld2=1.5bit/Symbol_.
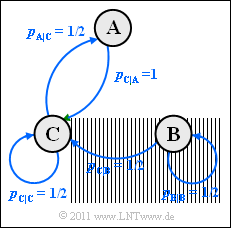
P ID2256 Inf Z 1 6e.png
5.  Aus nebenstehendem Übergangsdiagramm mit den aktuellen Parametern erkennt man, dass bei Stationarität pB = 0 gelten wird: B kann höchstens zum Starzeitpunkt einmal auftreten. Es liegt also eine binäre Markovkette mit den Symbolen A und C vor. Die Symbolwahrscheinlichkeiten ergeben sich zu:
pA=0.5⋅pC,pA+pC=1
⇒pA=1/3,pC=2/3.

Damit erhält man folgende Wahrscheinlichkeiten:
pA|A=0⇒pAA=0,pA|C=1/2⇒pCA=pC⋅pA|C=2/3⋅1/2=1/3,ld(1/pA|C)=1,pC|A=1⇒pAC=pA⋅pC|A=1/3⋅1=1/3,ld(1/pC|A)=0,pC|C=1/2⇒pCC=pC⋅pC|C=2/3⋅1/2=1/3,ld(1/pC|C)=1
⇒H=pAA⋅ld1pA|A+pCA⋅ld1pA|C+pAC⋅ld1pC|A+pCC⋅ld1pC|C==0+1/3⋅1+1/3⋅0+1/3⋅1=0.667bit/Symbol_.

Retrieved from "http://en.lntwww.de/index.php?title=Aufgaben:Exercise_1.6Z:_Ternary_Markov_Source&oldid=6753"
  • Powered by MediaWiki