Aufgaben:Exercise 3.10Z: BSC Channel Capacity

• Return to book

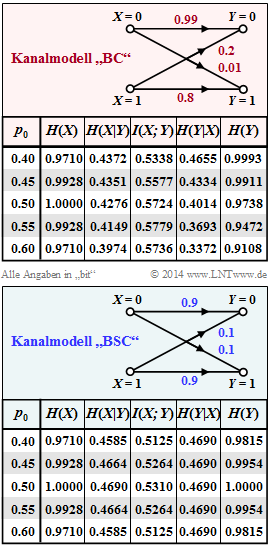
Die Kanalkapazität $C$ wurde von Claude $E$. Shannon als die maximale Transinformation definiert, wobei sich die Maximierung allein auf die Quellenstatistik bezieh $$ C = \max_{P_X(X)} \hspace{0.15cm} I(X;Y) \hspace{0.05cm}$$ Beim Binärkanal mit der Wahrscheinlichkeitsfunktion $P_X(X) = [p_0, p:1]$ ist nur ein Parameter optimierbar, beispielsweise $p_0$. Die Wahrscheinlichkeit für eine $„1”$ ist damit ebenfalls festgelegt: $p_1 = 1 – p_0$

Die obere Grafik (rot hinterlegt) fasst die Ergebnisse für den unsymmetrischen Binärkanal mit $ε_0 = 0.01$ und $ε_1 = 0.2$ zusammen, der im Theorieteil betrachtet wurde. Die Maximierung führt zum Ergebnis $p_0 = 0.55$

$\Rightarrow p_1 = 0.45$, und man erhält für die Kanalkapazität: $$C_{\rm BC} = \hspace{-0.05cm} \max_{P_X(X)} \hspace{0.1cm} I(X;Y) \big |_{p_0 \hspace{0.05cm} = \hspace{0.05cm}0.55} \hspace{0.05cm}=\hspace{0.05cm} 0.5779\,{\rm bit} \hspace{0.05cm}$$

In der unteren Grafik (blaue Hinterlegung) sind die gleichen informationstheoretischen Größen für den symmetrischen Kanal $\Rightarrow$ Binary Symmetric Channel (BSC) mit den Verfälschungswahrscheinlichkeiten $ε1 = ε2 = ε = 0.1$ angegeben, der auch für die Aufgabe A3.9 vorausgesetzt wurde.

In der vorliegenden Aufgabe sollen Sie für das BSC–Kanalmodell (zunächst für $ε = 0\ cdot 1$)

• die Entropien $H(X)$, $H(Y)$, $H(X|Y)$, $H(Y|X)$ analysieren,
• den Quellenparameter $p_0$ hinsichtlich maximaler Transinformation $I(X; Y)$ optimieren,
• somit die Kanalkapazität $C(ε)$ bestimmen, sowie
• durch Verallgemeinerung eine geschlossene Gleichung für $C(ε)$ angeben.

Hinweis: Die Aufgabe bezieht sich auf die Thematik von Kapitel 3.3

Fragebogen

1

Berechnen Sie die Quellenentropie allgemein und für $p_0 = 0.4.$

$p_0 = 0.4: H(X)$ = $bit$

2

Berechnen Sie die Sinkenentropie allgemein und für $p_0 = 0.4.$

$p_0 = 0 \cdot 4: H(Y)$ = $bit$

3

Berechnen Sie die Verbundentropie allgemein und für $p_0 = 0.4.$

$p_0 = 0\cdot 4: H(XY)$ = $bit$

4

Berechnen Sie die Transinformation allgemein und für $p_0 = 0.4.$

$p_0 = 0\cdot 4: I(X; Y)$ = $bit$

5

Welche Wahrscheinlichkeit $p_0$ führt zur Kanalkapazität $C$?

$ Maximierung: p_0$ =

6

Wie groß ist die Kanalkapazität des vorliegenden Kanals?

$C$ = $bit$

7

Wie groß sind die bedingten Entropien?

$p_0 gemäß (e): H(X|Y)$ = $bit$

$H(Y|X)$ = $bit$

Musterlösung

Solution

1. Aus der Tabelle auf der Angabenseite erkennt man, dass beim BSC–Modell (blaue Hinterlegung) wie auch beim allgemeineren (unsymmetrischen) BC–Modell (rote Hinterlegung) die Äquivokation $H(X|Y)$ von den Quellensymbolwahrscheinlichkeiten $p_0$ und $p_1$ abhängt. Daraus folgt, dass der Lösungsvorschlag 1 nicht richtig sein kann. Dagegen ist die Irrelevanz $H(Y|X)$ unabhängig von der Quellenstatistik, so dass auch der Lösungsvorschlag 3 ausgeschlossen werden kann.

Richtig ist vielmehr der Lösungsvorschlag 2, wie die folgende Rechnung zeigt: $$H(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X) \hspace{-0.15cm} =\hspace{-0.15cm} p_0 \cdot (1 - \varepsilon) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{1 - \varepsilon} + p_0 \cdot \varepsilon \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{\varepsilon} +$$ $$ \hspace{-0.15cm} p_1 \cdot \varepsilon \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{\varepsilon} + p_1 \cdot (1 - \varepsilon) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{1 - \varepsilon} =$$ $$=\hspace{-0.15cm} (p_0 + p_1) \cdot \left [ \varepsilon \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{\varepsilon} + (1 - \varepsilon) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{1 - \varepsilon} \right ] \hspace{0.05cm}.$$ Mit $p_0 + p_1 = 1$n und der binären Entropiefunktion $\Rightarrow H_{bin}$ erhält man das vorgeschlagene Ergebnis: $$H(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X) = H_{\rm bin}(\varepsilon)\hspace{0.05cm}$$ Für $ε = 0.1$ ergibt sich $H(Y|X) = 0.4690 bit$. Der gleiche Wert steht für alle $p_0$ in der gegebenen Tabelle. 2. Zutreffend sind hier alle vorgegebenen Lösungsalternativen. Die Kanalkapazität ist definiert als die maximale Transinformation, wobei die Maximierung hinsichtlich $P_X = (p_0, p_1)$ zu erfolgen hat: $$C = \max_{P_X(X)} \hspace{0.15cm} I(X;Y) \hspace{0.05cm}$$ Diese Gleichung gilt allgemein, also auch für den rot hinterlegten unsymmetrischen Binärkanal (BC).

Die Transinformation kann zum Beispiel allgemein wie folgt berechnet werden: $$I(X;Y) = H(Y) - H(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X)\hspace{0.05cm}$$ 3. 4. 5. 6. 7.