Difference between revisions of "Aufgaben:Exercise 3.11Z: Extremely Asymmetrical Channel"
(Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Informationstheorie/Anwendung auf die Digitalsignalübertragung }} [[File:|right|]] ===Fragebogen=== <quiz display=simple> {Multi…“) |
|||
| Line 3: | Line 3: | ||
}} | }} | ||
| − | [[File:|right|]] | + | [[File:P_ID2800__Inf_Z_3_10.png|right|]] |
| − | + | Betrachtet wird der nebenstehend gezeichnete Kanal mit den folgenden Eigenschaften: | |
| + | :* Das Symbol $X = 0$ wird immer richtig übertragen und führt stets zum Ergebnis $Y = 0$. | ||
| + | :* Das Symbol $X = 1$ wird maximal verfälscht. Aus Sicht der Informationstheorie bedeutet diese Aussage: | ||
| + | $${\rm Pr}(Y \hspace{-0.05cm} = 0\hspace{-0.05cm}\mid \hspace{-0.05cm} X \hspace{-0.05cm}= 1) ={\rm Pr}(Y \hspace{-0.05cm} = 1\hspace{-0.05cm}\mid \hspace{-0.05cm} X \hspace{-0.05cm}= 1) = 0.5 \hspace{0.05cm}$$ | ||
| + | Zu bestimmen sind in dieser Aufgabe: | ||
| + | :* die Transinformation $I(X; Y)$für $P_X(0) = p_0 = 0.4$ und $P_X(1) = p_1 = 0.6$. Es gilt allgemein: | ||
| + | $$ I(X;Y) \hspace{-0.15cm} =\hspace{-0.15cm} H(X) - H(X \hspace{-0.1cm}\mid \hspace{-0.1cm} Y)\hspace{0.05cm}$$ | ||
| + | $$I(X;Y) \hspace{-0.15cm} = \hspace{-0.15cm} H(Y) - H(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X)\hspace{0.05cm}$$ | ||
| + | $$I(X;Y) \hspace{-0.15cm} =\hspace{-0.15cm} H(X) + H(Y)- H(XY)\hspace{0.05cm}$$ | ||
| + | :* die Kanalkapazität: | ||
| + | $$ C = \max_{P_X(X)} \hspace{0.15cm} I(X;Y) \hspace{0.05cm}$$ | ||
| + | '''Hinweis:''' Die Aufgabe beschreibt einen Teilaspekt von [http://en.lntwww.de/Informationstheorie/Anwendung_auf_die_Digitalsignal%C3%BCbertragung Kapitel 3.3]. In der Aufgabe A3.13 sollen die hier gefundenen Ergebnisse im Vergleich zum BSC–Kanal interpretiert werden | ||
===Fragebogen=== | ===Fragebogen=== | ||
Revision as of 16:16, 28 November 2016
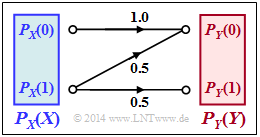
Betrachtet wird der nebenstehend gezeichnete Kanal mit den folgenden Eigenschaften:
- Das Symbol $X = 0$ wird immer richtig übertragen und führt stets zum Ergebnis $Y = 0$.
- Das Symbol $X = 1$ wird maximal verfälscht. Aus Sicht der Informationstheorie bedeutet diese Aussage:
$${\rm Pr}(Y \hspace{-0.05cm} = 0\hspace{-0.05cm}\mid \hspace{-0.05cm} X \hspace{-0.05cm}= 1) ={\rm Pr}(Y \hspace{-0.05cm} = 1\hspace{-0.05cm}\mid \hspace{-0.05cm} X \hspace{-0.05cm}= 1) = 0.5 \hspace{0.05cm}$$ Zu bestimmen sind in dieser Aufgabe:
- die Transinformation $I(X; Y)$für $P_X(0) = p_0 = 0.4$ und $P_X(1) = p_1 = 0.6$. Es gilt allgemein:
$$ I(X;Y) \hspace{-0.15cm} =\hspace{-0.15cm} H(X) - H(X \hspace{-0.1cm}\mid \hspace{-0.1cm} Y)\hspace{0.05cm}$$ $$I(X;Y) \hspace{-0.15cm} = \hspace{-0.15cm} H(Y) - H(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X)\hspace{0.05cm}$$ $$I(X;Y) \hspace{-0.15cm} =\hspace{-0.15cm} H(X) + H(Y)- H(XY)\hspace{0.05cm}$$
- die Kanalkapazität:
$$ C = \max_{P_X(X)} \hspace{0.15cm} I(X;Y) \hspace{0.05cm}$$ Hinweis: Die Aufgabe beschreibt einen Teilaspekt von Kapitel 3.3. In der Aufgabe A3.13 sollen die hier gefundenen Ergebnisse im Vergleich zum BSC–Kanal interpretiert werden
Fragebogen
Musterlösung