Difference between revisions of "LNTwww:Authors"
| Line 7: | Line 7: | ||
==Signaldarstellung== | ==Signaldarstellung== | ||
| + | * Entstanden zwischen ??? | ||
* Autoren: Günter Söder und Klaus Eichin | * Autoren: Günter Söder und Klaus Eichin | ||
* Weitere Beteiligte des LNT: | * Weitere Beteiligte des LNT: | ||
| − | * Mitarbeit von Studenten: | + | * Mitarbeit von Studenten: Huber |
| − | == | + | ==Lineare zeitinvariante Systeme== |
| − | |||
| − | + | * Entstanden zwischen ??? | |
| − | * | + | * Autoren: Günter Söder und Klaus Eichin |
| − | * | + | * Weitere Beteiligte des LNT: |
| − | + | * Mitarbeit von Studenten: Huber | |
| − | |||
| − | * | ||
| − | : | ||
| − | * | ||
| − | |||
| − | : | ||
| − | |||
| − | |||
==Übertragungsfunktion - Frequenzgang== | ==Übertragungsfunktion - Frequenzgang== | ||
Revision as of 14:28, 29 November 2016
Das Lerntutorial LNTwww wird vom Lehrstuhls für Nachrichtentechnik (LNT) der Technischen Universität München (TUM) angeboten. Alle Rechte an diesem Tutorial verbleiben bei LNT/TUM und den nachfolgend genannten Autoren.
Weiteres BLABLA
Contents
Signaldarstellung
- Entstanden zwischen ???
- Autoren: Günter Söder und Klaus Eichin
- Weitere Beteiligte des LNT:
- Mitarbeit von Studenten: Huber
Lineare zeitinvariante Systeme
- Entstanden zwischen ???
- Autoren: Günter Söder und Klaus Eichin
- Weitere Beteiligte des LNT:
- Mitarbeit von Studenten: Huber
Übertragungsfunktion - Frequenzgang
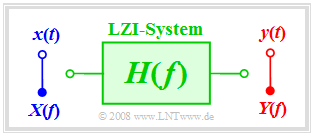
Wir setzen ein LZI–System voraus, dessen Eingangs– und Ausgangsspektrum $X(f)$ bzw. $Y(f)$ bekannt sind oder aus den Zeitsignalen $x(t)$ und $y(t)$ durch Fouriertransformation berechnet werden können.
Das Übertragungsverhalten eines Nachrichtensystems wird im Frequenzbereich durch die Übertragungsfunktion beschrieben: $$H(f) = \frac{Y(f)}{X(f)}= \frac{ {\rm Wirkungsfunktion}}{ {\rm Ursachenfunktion}}.$$ Weitere Bezeichnungen für $H(f)$ sind Systemfunktion und Frequenzgang. Im Folgenden werden wir vorwiegend den letzten Begriff verwenden.
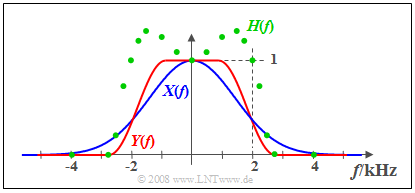
Am Eingang eines LZI–Systems liegt das Signal $x(t)$ mit dem rein reellen Spektrum $X(f)$ an (blaue Kurve). Das gemessene Ausgangsspektrum $Y(f)$ – in der Grafik rot markiert – ist bei Frequenzen kleiner als 2 kHz größer als $X(f)$ und besitzt im Bereich um 2 kHz eine steilere Flanke. Oberhalb von 2.8 kHz hat das Signal $y(t)$ keine Spektralanteile.
Die grünen Kreise markieren einige Messpunkte des ebenfalls reellen Frequenzgangs $H(f)$ = $Y(f)/X(f)$. Bei niedrigen Frequenzen ist $H(f)$ größer als 1, das heißt, in diesem Bereich wirkt das LZI–System verstärkend. Der Flankenabfall von $H(f)$ verläuft ähnlich wie der von $Y(f)$, ist aber nicht identisch mit diesem.
Eigenschaften des Frequenzgangs
Der Frequenzgang $H(f)$ ist eine zentrale Größe bei der Beschreibung nachrichtentechnischer Systeme. Nachfolgend werden einige Eigenschaften dieser wichtigen Systemgröße aufgezählt:
- Der Frequenzgang beschreibt allein das System. Er ist zum Beispiel aus den linearen Bauelementen eines elektrischen Netzwerks berechenbar. Bei anderem Eingangssignal $x(t)$ und dementsprechend anderem Ausgangssignal $y(t)$ ergibt sich der genau gleiche Frequenzgang $H(f)$.
- $H(f)$ kann auch eine Einheit besitzen. Betrachtet man zum Beispiel bei einem Zweipol den Spannungsverlauf $u(t)$ als Ursache und den Strom $i(t)$ als Wirkung, so hat der Frequenzgang $H(f)$ = $I(f)/U(f)$ die Einheit A/V. $I(f)$ und $U(f)$ sind die Fouriertransformierten von $i(t)$ bzw. $u(t)$.
- Im Folgenden betrachten wir ausschließlich Vierpole. Zudem setzen wir ohne Einschränkung der Allgemeingültigkeit meist voraus, dass $x(t)$ und $y(t)$ jeweils Spannungen seien. In diesem Fall ist $H(f)$ stets dimensionslos.
- Da die Spektren $X(f)$ und $Y(f)$ im Allgemeinen komplex sind, ist auch der Frequenzgang $H(f)$ eine komplexe Funktion. Man bezeichnet den Betrag $\\ |H(f)|$ als Amplitudengang. Dieser wird auch oft in logarithmierter Form dargestellt und als Dämpfungsverlauf bezeichnet:
- $$a(f) = - \ln |H(f)| = - 20 \cdot \lg |H(f)|.$$
- Je nachdem, ob die erste Form mit dem natürlichen oder die zweite mit dekadischem Logarithmus verwendet wird, ist die Pseudoeinheit „Neper” (Np) bzw. „Dezibel” (dB) hinzuzufügen.
- Der Phasengang ist aus $H(f)$ in folgender Weise berechenbar:
- $$b(f) = - {\rm arc} \hspace{0.1cm}H(f) \hspace{0.2cm}{\rm in\hspace{0.1cm}Radian \hspace{0.1cm}(rad)}.$$
- Damit kann der gesamte Frequenzgang auch wie folgt dargestellt werden:
- $$H(f) = |H(f)| \cdot {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot\hspace{0.05cm} b(f)} = {\rm e}^{-a(f)}\cdot {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm} b(f)}.$$
Tiefpass, Hochpass, Bandpass und Bandsperre
Nach dem Amplitudengang $|H(f)|$ unterscheidet man zwischen
- Tiefpass: Signalanteile werden mit zunehmender Frequenz in der Tendenz stärker gedämpft.
- Hochpass: Hier werden hochfrequente Signalanteile weniger gedämpft als niederfrequente. Ein Gleichsignal (also ein Signalanteil mit der Frequenz $f = 0$) kann über einen Hochpass nicht übertragen werden.
- Bandpass: Es gibt eine bevorzugte Frequenz, die man als Mittenfrequenz $f_{\rm M}$ bezeichnet. Je weiter die Frequenz eines Signalanteils von $f_{\rm M}$ entfernt ist, um so stärker wird dieser gedämpft.
- Bandsperre: Dies ist das Gegenstück zum Bandpass und es gilt $|H(f_{\rm M})| ≈ 0$. Sehr niederfrequente und sehr hochfrequente Signalanteile werden dagegen gut durchgelassen.
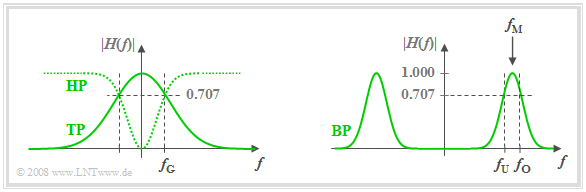
Die Grafik zeigt die Amplitudengänge der Filtertypen TP und HP (links) sowie BP (rechts). Ebenfalls eingezeichnet sind die Grenzfrequenzen $f_{\rm G}$ (bei Tiefpass und Hochpass) bzw. $f_{\rm U}$ und $f_{\rm O}$ (beim Bandpass). Diese bezeichnen hier 3dB–Grenzfrequenzen, zum Beispiel gemäß folgender Definition:
Die 3dB–Grenzfrequenz eines Tiefpasses gibt diejenige Frequenz $f_{\rm G}$ an, für die gilt: $$|H(f = f_{\rm G})| = {1}/{\sqrt{2}} \cdot|H(f = 0)| \hspace{0.5cm}\Rightarrow\hspace{0.5cm} |H(f = f_{\rm G})|^2 = {1}/{2} \cdot|H(f = 0)|^2.$$
Anzumerken ist, dass es für Grenzfrequenzen auch andere Definitionen gibt. Diese finden Sie auf der Seite Allgemeine Bemerkungen
im Kapitel „Einige systemtheoretische Tiefpassfunktionen” .
Testsignale zur Messung von H(f)
Zur messtechnischen Erfassung des Frequenzgangs $H(f)$ eignet sich jedes beliebige Eingangssignal $x(t)$ mit Spektrum $X(f)$, solange $X(f)$ keine Nullstellen aufweist. Durch Messung des Ausgangsspektrums $Y(f)$ lässt sich so der Frequenzgang in einfacher Weise ermitteln: $$H(f) = \frac{Y(f)}{X(f)}.$$ Insbesondere sind folgende Eingangssignale besonders geeignet:
- Diracimpuls $x(t) = K · δ(t)$ ⇒ Spektrum $X(f) = K$:
- Somit ist der Frequenzgang nach Betrag und Phase formgleich mit dem Ausgangsspektrum $Y(f)$ und es gilt $H(f) = 1/K · Y(f)$. Approximiert man den Diracimpuls durch ein schmales Rechteck gleicher Fläche $K$, so muss $H(f)$ mit Hilfe einer ${\rm sin}(x)/x$–Funktion korrigiert werden.
- Diracpuls – die unendliche Summe gleichgewichteter Diracimpulse im zeitlichen Abstand $T_{\rm A}$:
- Dieser führt gemäß Kapitel Zeitdiskrete Signaldarstellung im Buch „Signaldarstellung” zu einem Diracpuls im Frequenzbereich mit Abstand $f_{\rm A} =1/T_{\rm A}$. Damit ist eine frequenzdiskrete Messung von $H(f)$ möglich, mit den spektralen Abtastwerten im Abstand $f_{\rm A}$.
- Harmonische Schwingung $x(t) = A_x · \cos (2πf_0t – φ_x)$ ⇒ diracförmiges Spektrum bei $\pm f_0$:
- Das Ausgangssignal $y(t) = A_y · \cos(2πf_0t – φ_y)$ ist eine Schwingung mit gleicher Frequenz $f_0$. Der Frequenzgang lautet für $f_0 \gt 0$:
- $$H(f_0) = \frac{Y(f_0)}{X(f_0)} = \frac{A_y}{A_x}\cdot{\rm e}^{\hspace{0.05cm} {\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} (\varphi_x - \varphi_y)}.$$ Um den frequenzkontinuierlichen Frequenzgang $H(f)$ zu ermitteln, sind allerdings (unendlich) viele Messungen mit unterschiedlichen Frequenzen $f_0$ erforderlich.
Signaldarstellung
- Autoren: Günter Söder und Klaus Eichin
- Weitere Beteiligte des LNT:
- Mitarbeit von Studenten:
Lineare zeitinvariante Systeme
- Autoren: Günter Söder und Klaus Eichin
- Weitere Beteiligte des LNT:
- Mitarbeit von Studenten:
Inhalt