Difference between revisions of "Aufgaben:Exercise 1.4: "Pointer diagram" and "Locality Curve""
| Line 2: | Line 2: | ||
{{quiz-Header|Buchseite=Modulationsverfahren/ Allgemeines Modell der Modulation}} | {{quiz-Header|Buchseite=Modulationsverfahren/ Allgemeines Modell der Modulation}} | ||
[[File:P_ID966__Mod_A_1_4_neu.png|right|]] | [[File:P_ID966__Mod_A_1_4_neu.png|right|]] | ||
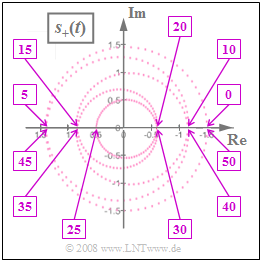
| − | Die beiliegende Grafik zeigt das analytische Signal $ | + | Die beiliegende Grafik zeigt das analytische Signal $s_+(t)$ in der komplexen Ebene. Die in den Rechtecken angegebenen Zahlenwerte geben die Zeitpunkte in Mikrosekunden an. Bei allen Vielfachen von $5 μs$ ist $s_+(t)$ stets reell und hat dabei folgende Werte: |
$$s_+(t = 0) =s_+(t = 50\;{\rm \mu s})= 1.500\hspace{0.05cm},\\ s_+(t = 5\;{\rm \mu s}) = s_+(t = 45\;{\rm \mu s})= -1.405\hspace{0.05cm},\\ s_+(t = 10\;{\rm \mu s}) = s_+(t = 40\;{\rm \mu s})= 1.155\hspace{0.05cm},\\ ... = ...\\ s_+(t = 25\;{\rm \mu s}) = -0.500\hspace{0.05cm}.$$ | $$s_+(t = 0) =s_+(t = 50\;{\rm \mu s})= 1.500\hspace{0.05cm},\\ s_+(t = 5\;{\rm \mu s}) = s_+(t = 45\;{\rm \mu s})= -1.405\hspace{0.05cm},\\ s_+(t = 10\;{\rm \mu s}) = s_+(t = 40\;{\rm \mu s})= 1.155\hspace{0.05cm},\\ ... = ...\\ s_+(t = 25\;{\rm \mu s}) = -0.500\hspace{0.05cm}.$$ | ||
Als bekannt vorausgesetzt werden kann, dass das dazugehörige physikalische Signal folgende Form hat: | Als bekannt vorausgesetzt werden kann, dass das dazugehörige physikalische Signal folgende Form hat: | ||
| Line 12: | Line 12: | ||
'''Hinweis:''' Die Aufgabe bezieht sich auf das [http://en.lntwww.de/Modulationsverfahren/Allgemeines_Modell_der_Modulation Kapitel 1.3] dieses Buches. Weitere Informationen zu dieser Thematik finden Sie in [http://en.lntwww.de/Signaldarstellung/Harmonische_Schwingung Kapitel 2.3] – [http://en.lntwww.de/Signaldarstellung/Analytisches_Signal_und_zugeh%C3%B6rige_Spektralfunktion Kapitel 4.2] – [http://en.lntwww.de/Signaldarstellung/%C3%84quivalentes_Tiefpass-Signal_und_zugeh%C3%B6rige_Spektralfunktion Kapitel 4.3] des Buches „Signaldarstellung” sowie den folgenden Interaktionsmodulen: | '''Hinweis:''' Die Aufgabe bezieht sich auf das [http://en.lntwww.de/Modulationsverfahren/Allgemeines_Modell_der_Modulation Kapitel 1.3] dieses Buches. Weitere Informationen zu dieser Thematik finden Sie in [http://en.lntwww.de/Signaldarstellung/Harmonische_Schwingung Kapitel 2.3] – [http://en.lntwww.de/Signaldarstellung/Analytisches_Signal_und_zugeh%C3%B6rige_Spektralfunktion Kapitel 4.2] – [http://en.lntwww.de/Signaldarstellung/%C3%84quivalentes_Tiefpass-Signal_und_zugeh%C3%B6rige_Spektralfunktion Kapitel 4.3] des Buches „Signaldarstellung” sowie den folgenden Interaktionsmodulen: | ||
| + | Zeigerdiagramm – Darstellung des analytischen Signals | ||
| + | |||
| + | Ortskurve – Verlauf des äquivalenten Tiefpass-Signals | ||
| + | |||
| + | |||
| + | In unserem Tutorial LNTwww wird die Darstellung des analytischen Signals $s_+(t)$ in der komplexen Ebene teilweise auch als „Zeigerdiagramm” bezeichnet, während die „Ortskurve” den zeitlichen Verlauf des äquivalenten TP–Signals $s_{TP}(t)$ angibt. | ||
===Fragebogen=== | ===Fragebogen=== | ||
Revision as of 14:11, 23 December 2016
Die beiliegende Grafik zeigt das analytische Signal $s_+(t)$ in der komplexen Ebene. Die in den Rechtecken angegebenen Zahlenwerte geben die Zeitpunkte in Mikrosekunden an. Bei allen Vielfachen von $5 μs$ ist $s_+(t)$ stets reell und hat dabei folgende Werte: $$s_+(t = 0) =s_+(t = 50\;{\rm \mu s})= 1.500\hspace{0.05cm},\\ s_+(t = 5\;{\rm \mu s}) = s_+(t = 45\;{\rm \mu s})= -1.405\hspace{0.05cm},\\ s_+(t = 10\;{\rm \mu s}) = s_+(t = 40\;{\rm \mu s})= 1.155\hspace{0.05cm},\\ ... = ...\\ s_+(t = 25\;{\rm \mu s}) = -0.500\hspace{0.05cm}.$$ Als bekannt vorausgesetzt werden kann, dass das dazugehörige physikalische Signal folgende Form hat: $$s(t) = A_{\rm T} \cdot \cos \left(\omega_{\rm T}\cdot t\right) + \frac{A_0}{2}\cdot \cos\left(\left(\omega_{\rm T} + \omega_{\rm 0}\right)\cdot t \right) + \frac{A_0}{2}\cdot \cos\left(\left(\omega_{\rm T} - \omega_{\rm 0}\right)\cdot t \right)\hspace{0.05cm}.$$ Gegeben ist weiterhin die Frequenz des Trägersignals zu $f_T = 100 kHz$. Ermittelt werden sollen die drei weiteren Parameter $f_0$, $A_T$ und $A_0$.
Bezug genommen wird auch auf das äquivalente TP–Signal $s_{TP}(t)$, wobei folgender Zusammenhang mit dem analytischen Signal besteht: $$s_{\rm TP}(t) = s_+(t) \cdot {\rm e}^{-{\rm j}\hspace{0.03cm} \cdot \hspace{0.03cm}\omega_{\rm T}\cdot \hspace{0.05cm}t} \hspace{0.05cm}.$$ Hinweis: Die Aufgabe bezieht sich auf das Kapitel 1.3 dieses Buches. Weitere Informationen zu dieser Thematik finden Sie in Kapitel 2.3 – Kapitel 4.2 – Kapitel 4.3 des Buches „Signaldarstellung” sowie den folgenden Interaktionsmodulen:
Zeigerdiagramm – Darstellung des analytischen Signals
Ortskurve – Verlauf des äquivalenten Tiefpass-Signals
In unserem Tutorial LNTwww wird die Darstellung des analytischen Signals $s_+(t)$ in der komplexen Ebene teilweise auch als „Zeigerdiagramm” bezeichnet, während die „Ortskurve” den zeitlichen Verlauf des äquivalenten TP–Signals $s_{TP}(t)$ angibt.
Fragebogen
Musterlösung